Highlights

• New Attribute-Regularized VAE (AR-VAE) that encodes specific attributes along specific dimensions of the latent space, in a supervised manner;
• Compared to similar methods, AR-VAE as the following advantages:
  • has a simple formulation with few hyperparameters,
  • works with continuous data attributes, and
  • is agnostic to how the attributes are computed/obtained.

Introduction

The authors introduce a new method to tackle the already well-researched task of disentangling specific factors of the data, called attributes, in a supervised way.

The authors argue that their approach fits a specific type of problem, namely manipulating continuous attributes, for which current methods are not adapted and/or perform poorly:

• Unsupervised disentanglement learning (e.g. \(\beta\)-VAE, FactorVAE¹, \(\beta\)-TCVAE², etc.) requires post-training analysis to identify how attributes are encoded, and consequently how to manipulate them;
• Supervised regularization methods (e.g. Conditional VAEs, Fader networks³, etc.) generally don’t work well for continuous data attributes, like Fader networks that work with binary attributes.

Methods

The authors simply add what they call an “attribute regularization” loss to a standard \(\beta\)-VAE.

The attribute regularization loss is computed in a three step process. In the steps, attributes are denoted by \(a\), and \(r\) indicates a regularized dimension of the latent space.

1. Compute an attribute distance matrix \(D_a \in \mathbb{R}^{m \times m}\) on a training mini-batch:

   \[D_a (i,j) = a(\bm{x}_i) - a(\bm{x}_j)\]

2. Compute a similar distance matrix \(D_r \in \mathbb{R}^{m \times m}\) on the dimensions of the latent vectors that you want to regularize:

   \[D_r (i,j) = z_{i}^{r} - z_{j}^{r}\]

3. Compute the regularization loss from both matrices as:

   \[L_{r,a} = \text{MAE}(\text{tanh}(\delta D_r) - \text{sgn}(D_a))\]

   where \(\delta\) is a tunable hyperparameter that decides the spread of the posterior.

The overall loss function for AR-VAE thus becomes:

\[L_{\text{AR-VAE}} = L_{\text{recons}} + \beta L_{\text{KLD}} + \gamma \sum_{l=0}^{\mathbb{L}-1} L_{r_{l},a_{l}}\]

Data

The authors point out that most research on disentanglement learning uses image-based datasets. This results in methods being trained, tested and validated on a single domain. To test their method across a wider variety of data, the authors therefore used four datasets across two domains:

• Images
  • Morpho-MNIST
  • 2-d sprites
• Music
  • Measures extracted from the soprano parts of the J.S. Bach Chorales dataset (≈350 chorales)
  • Measures extracted (≈20,000) from folk melodies in the Scottish and Irish style

Results

The full paper contains extensive quantitative and qualitative results on the datasets, so only a very select subset is shown here.

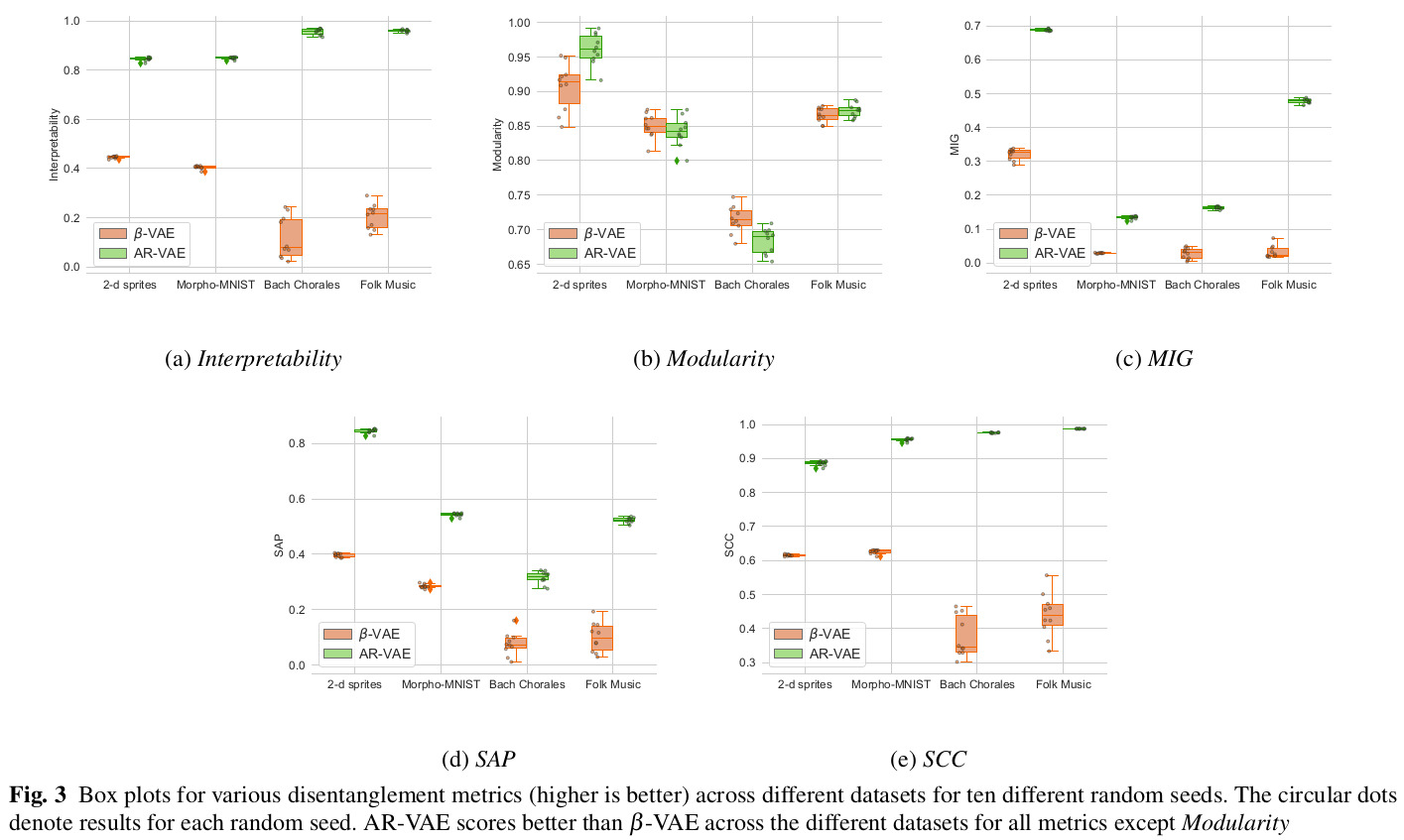
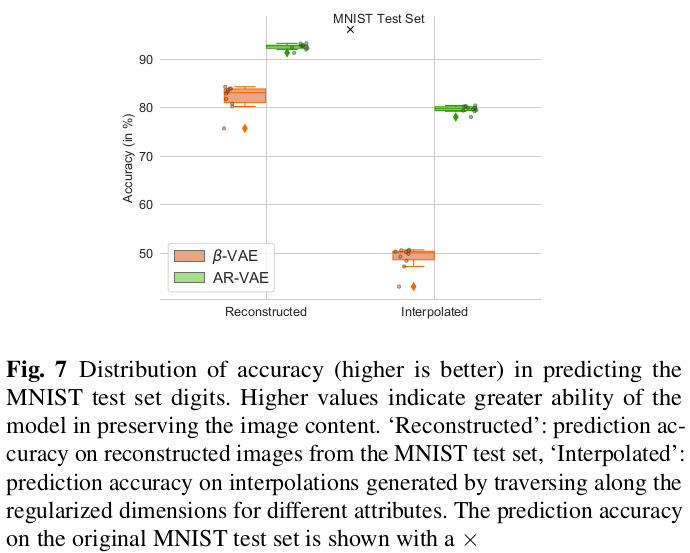
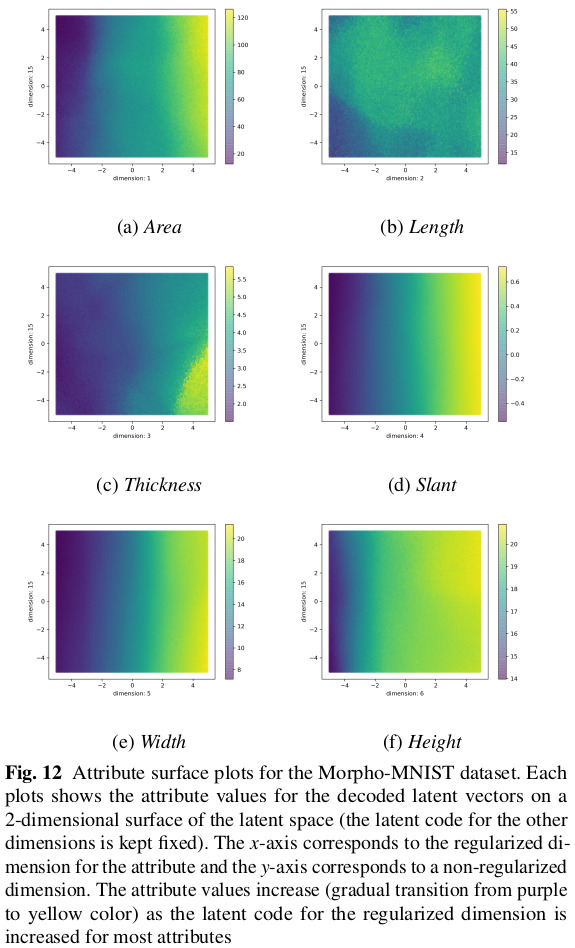
Remarks

• While empirically the attribute regularization seems to work well, theoretically it doesn’t constrain the network from encoding attribute-related information outside of their designated dimensions.

References