Highlights

• Novel FactorVAE, that provides higher disentanglement scores than \(\beta\)-VAE for the same reconstruction quality
• Novel disentanglement metric that is more robust than the previous widely-known metric proposed by Higgins et al.¹
• Quantitative comparisons between VAE-based methods (represented by FactorVAE and \(\beta\)-VAE) and an InfoGAN-based method (InfoWGAN-GP)

Introduction

The authors analyze the disentanglement and reconstruction aspects of \(\beta\)-VAE, which essentially allows to weight the KL divergence term in the classic VAE loss. The \(\beta\)-VAE objective can be formulated like follows, where \(\beta \geq 1\):

\[\frac{1}{N} \sum_{i=1}^{N} \Big[\mathbb{E}_{q(z|x^{(i)})}[\log p(x^{(i)}|z)] - \beta KL(q(z|x^{(i)})~\|~p(z))\Big]\]

The first term is the reconstruction error, and the second term is the complexity penalty. This second term can be reformulated like below, given \(q(z)\) the distribution of representations for the entire data set and \(I(x;z)\) the mutual information between an input \(x\) and its encoding \(z\) under the joint distribution \(p_{data}(x)q(z|x)\).

\[\mathbb{E}_{p_{data}(x)}[KL(q(z|x)~\|~p(z))] = I(x;z) + KL(q(z)~\|~p(z))\]

What this equivalent formulation highlights is that while penalizing the original KL divergence with \(\beta \geq 1\) term pushes \(q(z)\) towards \(p(z)\) (encouraging disentanglement), it also reduces the information about \(x\) stored in \(z\), and therefore the reconstruction accuracy. The authors state that penalizing \(I(x;z)\) “might be neither necessary nor desirable for disentangling”.

Methods

FactorVAE

Given the claim about the mutual information term, the authors propose to motivate FactorVAE with an objective that directly encourages the independence in the code distribution:

\[\frac{1}{N} \sum_{i=1}^{N} \Big[\mathbb{E}_{q(z|x^{(i)})}[\log p(x^{(i)}|z)] - KL(q(z|x^{(i)})~\|~p(z))\Big] - \gamma KL(q(z)~\|~\bar{q}(z))\]

where \(\bar{q}(z) = \prod_{j=1}^{d} q(z_{j})\). This is also a lower bound on the marginal log likelihood. \(KL(q(z)~\|~\bar{q}(z))\) is also known as Total Correlation (TC), and is intractable in this case, since it would require passing through the entire dataset for each evaluation.

To circumvent this issue, the authors explain that it is possible to sample from both \(q(z)\) and \(\bar{q}(z)\) (details on how to this are discussed in the paper), which then allows them to use the density-ratio trick to minimize the KL divergence. The density-ratio trick consists of training a discriminator \(D\) (in their case an MLP) to estimate whether a sample comes from \(q(z)\) or \(\bar{q}(z)\). This allows them to rephrase the TC as:

\[TC(z) = KL(q(z)~\|~\bar{q}(z)) = \mathbb{E}_{q(z)}\Bigg[\log \frac{q(z)}{\bar{q}(z)}\Bigg] \approx \mathbb{E}_{q(z)}\Bigg[\log \frac{D(z)}{1 - D(z)}\Bigg]\]

The discriminator and VAE are trained jointly, and the training algorithm for FactorVAE is given below:

As for the InfoWGAN-GP, it builds on top of InfoGAN, which is an alternative to \(\beta\)-VAE that learns disentangled representations. Little empirical comparisons exist between VAE-based methods and InfoGAN (due to GAN training stability issues). Therefore, the author implemented SOTA techniques for stabilizing GANs (namely, using the Wasserstein distance and gradient penalty) to derive InfoWGAN-GP from InfoGAN and fairly compare it to VAE-based methods.

Disentanglement Metric

The authors propose a new metric meant to overcome a major shortcoming of the currently accepted metric proposed by Higgins et al., which can give a perfect score when all but one dimension are disentangled. They claim their metric is more robust in this case, as well as being generally more intuitive. However, in both cases, the metrics only really work on synthetic data sets rather than realistic data sets, since they require knowing the “groundtruth” factoring in the data itself, and don’t allow for correlations among the factors or hierarchies over them.

Data

FactorVAE is compared to \(\beta\)-VAE on 2 data sets with known generative factors and 3 data sets with unknown generative factors (notably CelebA).

Results

Comparison of the reconstruction vs disentanglement trade-off in \(\beta\)-VAE and FactorVAE.

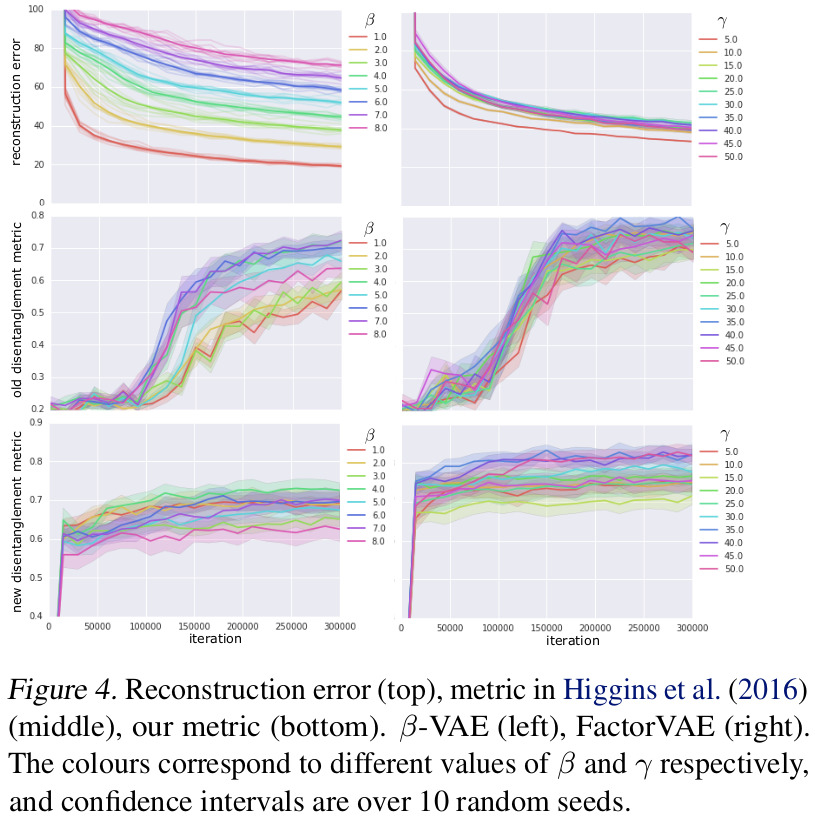
More results (on disentanglement metrics, TC and subjectively on other data sets) are available in the paper.

As for InfoWGAN-GP, its disentanglement results were disappointingly low. The authors theorize that their generator and discriminator architectures (similar to their VAEs) might not be adequate, since InfoGAN is known to be sensible to architecture. However, this in itself is a weakness when compared to VAE-based methods, which are more robust to architecture choice.

References