Highlights

• Novel term added to DQN’s target, akin to maximum-entropy reinforcement learning, achieving state-of-the-art results on the Atari Learning Environment suite

Baron Munchausen pulls himself out of a mire by his own hair.

source: https://en.wikipedia.org/wiki/M%C3%BCnchhausen_trilemma

Introduction

Reinforcement learning (RL) often uses bootstrapping when training agents: bootstrapping occurs when the target for computing a loss function leverages the network’s own estimates, like with Deep Q-Network (DQN)’s Temporal-Difference (TD) update:

\[\tag{1} L(\phi) = \mathbb{E}_{s,a,s',r \sim D}\big(\underbrace{r + \gamma \max_{a'}Q_{\phi'}(s', a')}_{\text{target}} - Q_\phi(s,a)\big)^2\]

The authors propose to leverage another estimate from the agent: its own policy. It is similar to maximum-entropy RL, which attempts to maximize both the expected return and the policy’s entropy by formulating the RL problem as:

\[\pi^* = \argmax_\pi \mathbb{E}\Big[\sum_{t=0}^\infty r_t + \alpha \mathbb{H}(\pi(\cdot||s_t))\Big],\]

leading to the (approximate)¹ following loss function for the Q-network:

\[L(\phi) = \mathbb{E}_{s,a,s',r \sim D}\big(\underbrace{r + \gamma \max_{a'}Q_{\phi'}(s', \hat{a}') - \tau \log \pi_\theta(\hat{a}'|s')}_{\text{target}} - Q_\phi(s,a)\big)^2, \hat{a}' \sim \pi_\theta(\cdot||s')\]

However, the authors propose not to subtract the log-policy to all rewards, but instead to “optimize for the immediate reward augmented by the log-policy”. Their motivations are as follows:

If the optimal Q-function \(Q^*(s,a)\) was known, the agent would use it as a target in equation \((1)\). However, it is unknown and the agent instead uses its own Q-function as an estimate. This is bootstrapping. If the optimal policy \(\pi^*\) was known, its log-probability for the optimal action would be \(0\), and \(-\infty\) otherwise. Because we don’t have the optimal policy, we can instead use the log-probabilities from our own policy to add to the reward signal.

Method:

Therefore, M-RL is as simple as replacing \(r_t\) with \(r_t + \alpha \log \pi(a_t{\mid}s_t)\) anytime TD is involved. Because M-RL supposes a stochastic policy and DQN typically trains implicit deterministic policies, the authors suggest two changes to the typical DQN update:

First, the policy is formulated as a softmax instead of a simple argmax so that the score (and its log) can be computed. This does not change the original DQN objective in any way. Second, they propose to turn the original DQN update into a Soft-DQN (as a reference to the Soft Actor-Critic² (SAC) algorithm) update:

\[L(\phi) = \mathbb{E}_{s,a,s',r \sim D}\big(r + \gamma \sum_{a' \in A} \pi_{\phi'}(a'|s')(Q_{\phi'}(s', a') - \tau \log \pi_{\phi'}(a'|s')) - Q_\phi(s,a)\big)^2, \\ \pi_{\phi'} = softmax(\frac{q_{\phi'}}{\tau})\]

which, the authors argue, is the same as a discrete action-space version of SAC. Now that the policy is properly stochastic (but maintaining that \(\tau \to 0\) would make the update equivalent to DQN), the scaled log-probability of the policy can be added to the reward to obtain the Munchausen-DQN (M-DQN) update:

\[L(\phi) = \mathbb{E}_{s,a,s',r \sim D}\big(r + \alpha \tau \log \pi_{\phi'}(a{\mid}s) + \gamma \sum_{a' \in A} \pi_{\phi'}(a'|s')(Q_{\phi'}(s', a') - \tau \log \pi_{\phi'}(a'|s')) - Q_\phi(s,a)\big)^2\]

Data

To test their method, the authors used all the 60 games from the Atari Learning Environment (ALE) suite.

Results

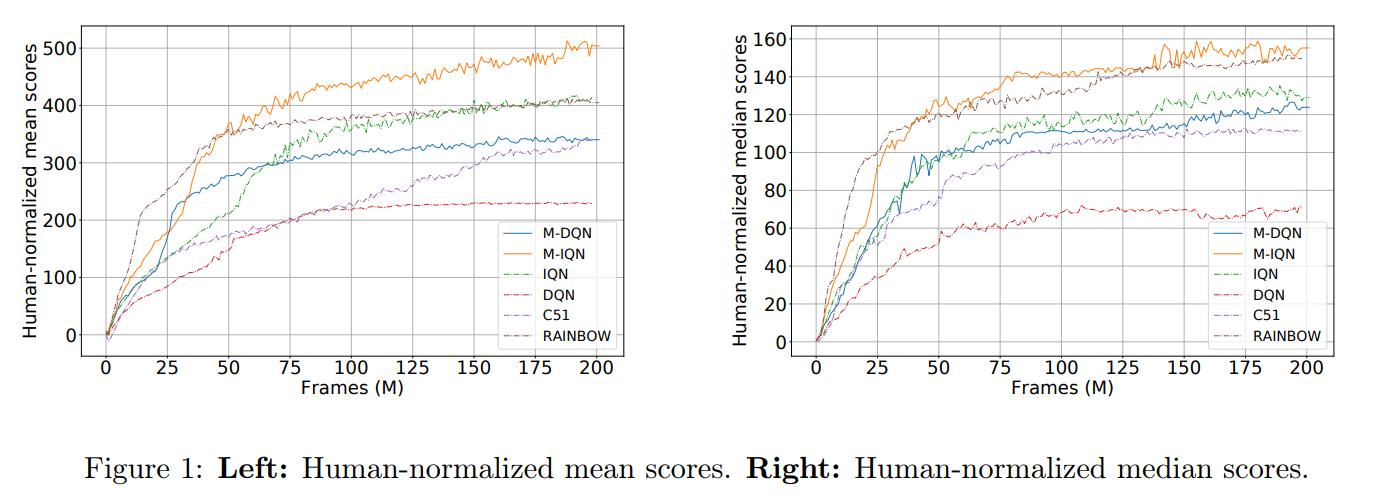
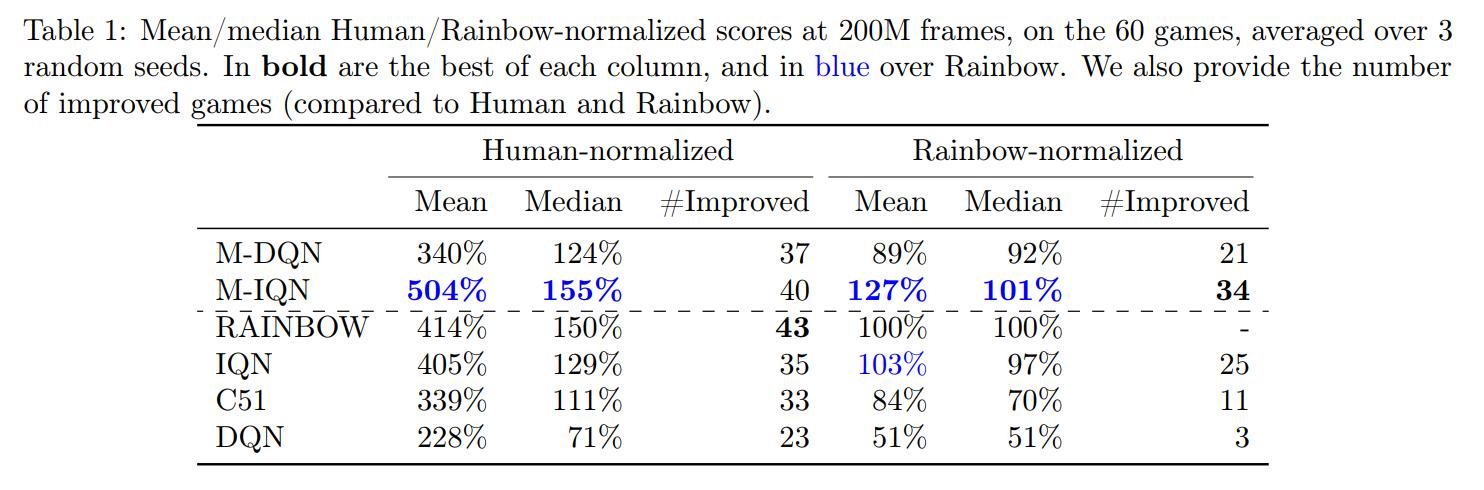
Despite being an extremely simple modification of DQN, M-DQN is very efficient. We show in Fig. 9 the Human-normalized mean and median scores for various agents on the full set of 60 Atari games of ALE […]. We observe that M-DQN significantly outperforms DQN, but also C51. As far we know, M-DQN is the first method that is not based on [distributional RL] which overtakes C51. These are quite encouraging empirical results.

M-IQN stands for Munchausen-IQN, their version of the distributional RL algorithm IQN³. We can see that M-IQN outperforms even Rainbow⁴, the aggregation of improvements made over the years to DQN (without the distributed part that led to NGU and Agent57)

Conclusions

This method augments the immediate rewards by the scaled logarithm of the policy computed by an RL agent. We applied this method to a simple variation of DQN, Soft-DQN, resulting in the M-DQN algorithm. M-DQN shows large performance improvements: it outperforms DQN on 53 of the 60 Atari games, while simply using a modification of the DQN loss. In addition, it outperforms the seminal distributional RL algorithm C51. We also extended the Munchausen idea to distributional RL, showing that it could be successfully combined with IQN to outperform the Rainbow baseline.

Remarks

• I wish the idea was also extended to continuous action-space algorithms like actually SAC or TD3. I guess it wouldn’t be too hard to do, if only I had time !
• I’m not sure I like the name. Even though its origin is kind of clever, it’s quite a mouthful.
• The paper provides a lot of theoretical insight (that I frankly glossed over) as to why this works

References