Highlights

• Reinforcement learning agent able to solve hard exploration games by learning a range of directed exploratory policies
• First algorithm to achieve non-zero rewards (with a mean score of 8,400) in the game of Pitfall! without using demonstrations or hand-crafted features

Introduction

The problem of exploration remains one of the major challenges in deep reinforcement learning.

A learning agent often needs to finetune a tradeoff between exploitation (acting on what it knows will work) and exploration (behaving in a way that is not guaranteed to be good) so as to learn a policy that achieves good reward without being stuck in a local optimum.

The first ideas for exploration were to have an \({\epsilon}-greedy\) policy (taking a random action with a probability of \(1-\epsilon\)) or to do Boltzmann exploration (exploring w.r.t the Q function of the state-action pair with a temperature parameter to decrease exploration over time). However, these methods are very inefficient in the context of larger non-tabular state-spaces.

Recent approaches have proposed to equip agents with an intrinsic reward promoting exploration (nicknamed “curiosity”), making them focus on exploring new, unseen states. As the agent explores its environment, the intrinsic motivation wears off and the reward becomes extrinsic. However, once a state has been visited, the agent is no longer encouraged to visit it again and therefore might not explore subsequent states that might have been more profitable. Finetuning the “curiosity” only seems to delay the problem.

Methods

The authors propose

\((i)\) defining an exploration bonus combining life-long and episodic novelty to learn exploratory strategies that can maintain exploration throughout the agent’s training process (to never give up), \((ii)\) to learn a family of policies that separate exploration and exploitation using a conditional architecture with shared weights

The never-give-up intrinsic reward

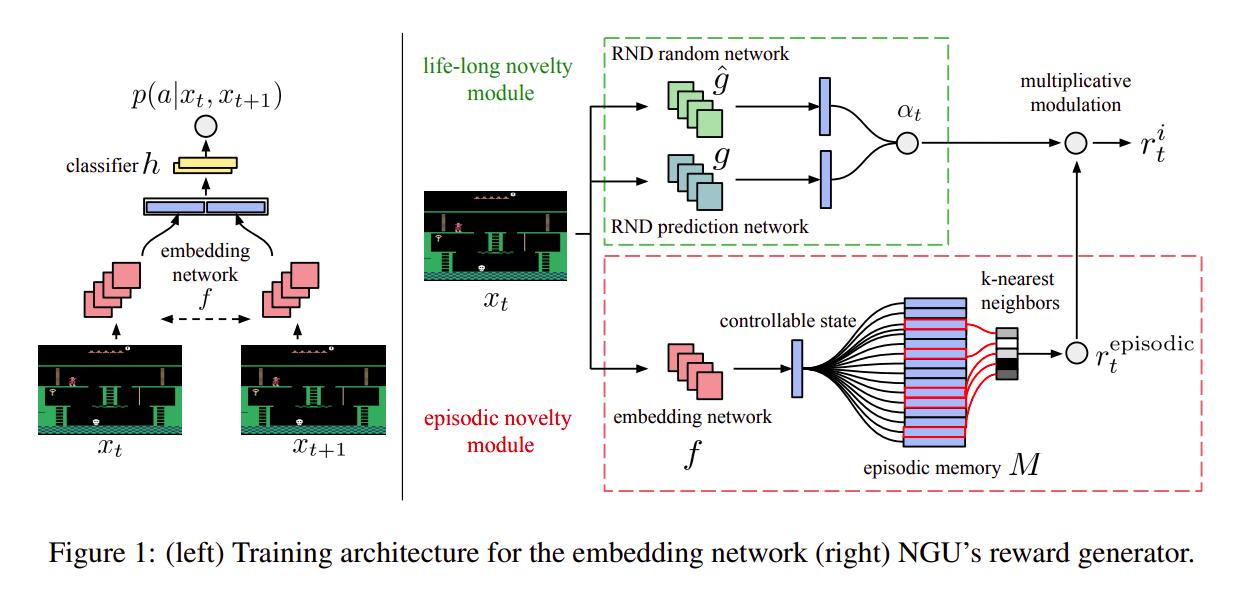
The network is trained on the augmented reward \(r_t = r_{t}^{e} + \beta{r_{t}^{i}}\). Figure 1 describes the intrinsic reward modules. The embedding network can be thought of a siamese network trained my maximizing \(p(a \mid x_t, x_{t+1})\). When used to embed states, the classifier and \(x_{t+1}\) are discarded. This allows the network to project the states into a space where as much useless information as possible has been discarded. The states are then saved in a buffer and clustered using k-NN so as to get a pseudo-count of the states. \(r_{t}^{episodic}\) is defined by

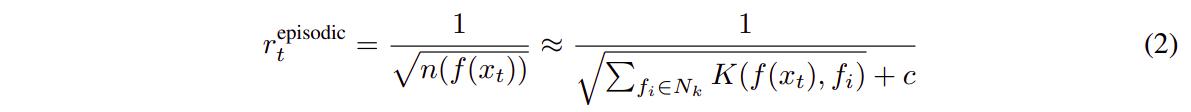
The article explains \(K\) in detail, but it is a riff on the euclidian distance between the “controlled states”.

The life-long novelty estimator is built using Random Network Distillation¹. Basically, a convolutional network \(g\) is trained to match the output of another randomly-initialized untrained CNN \(\hat{g}\). The \(\alpha\) parameter is a riff on the error \(\|\hat{g}(x_t;\theta) - g(x)\|^2\) so that as \(\hat{g}\) sees the episode more and more, its error decreases and so does \(\alpha_t\).

The never-give-up agent

Using intrinsic reward means changing the underlying MDP.

If the augmented reward \(r_t = r_{t}^{e} + {\beta}{r_{t}^{i}}\) varies in ways unpredictable from the action and states, then the decision process may no longer be a MDP, but instead be a Partially Observed MDP (POMDP).

To alleviate the problem, the authors \((i)\) use a recurrent agent based on R2D2² and \((ii)\) also feed the intrinsic reward, amongst other things, as an input to the network.

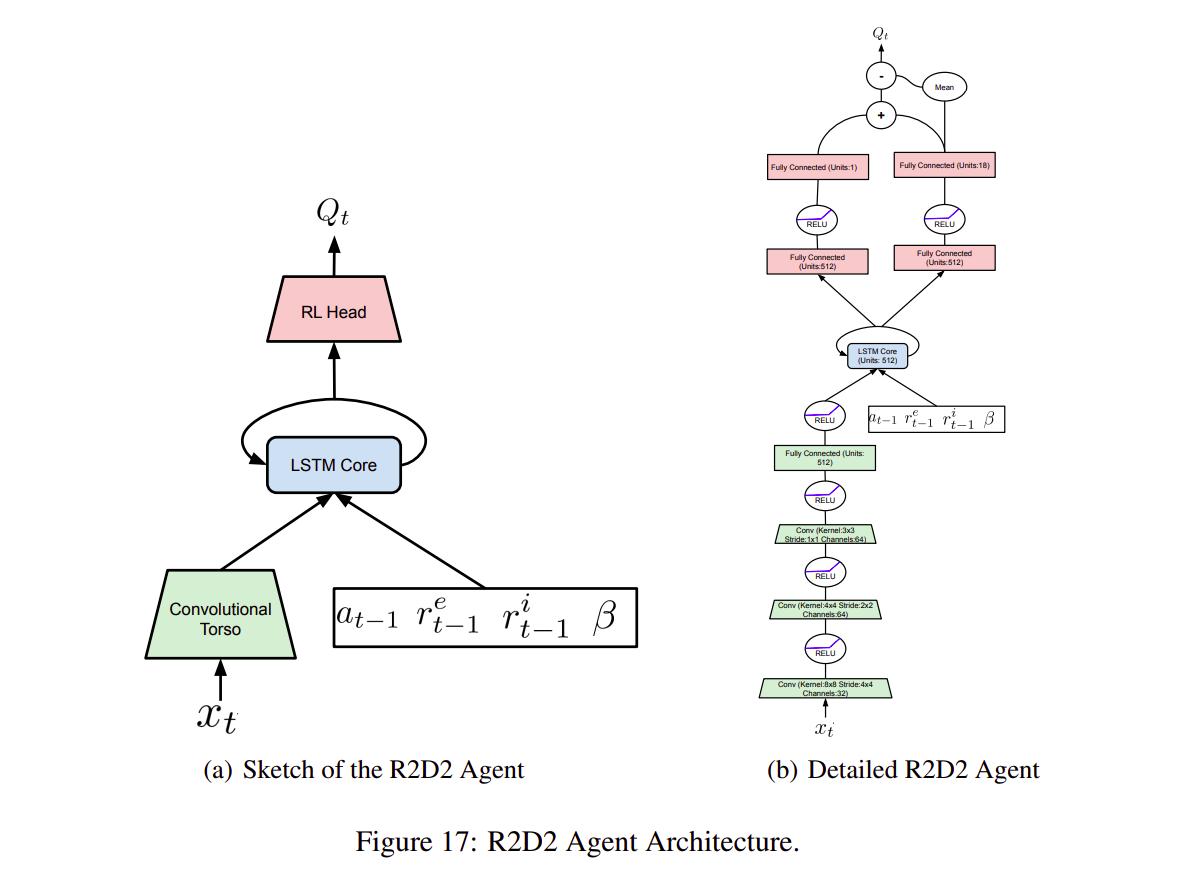
To train a variety of exploring and exploiting policies, the authors use a universal value function approximator (UVFA)³ \(Q(x, a, \beta)\) to approximate the optimal value function w.r.t the reward of the form \(r_t = r_{t}^{e} + {\beta}{_i}{r_{t}^{i}}\) where \(\beta{_i}\) is apart of a family of \(N\) values \(\{\beta{_i}\}_{i=0}^{N-1}\) including \(\beta_{0} = 0\). Having a large N means having a greater variety in behavior and therefore more efficient training.

Experiments

The authors tested on the Atari suite as well as their own new environment: Random Disco Maze.

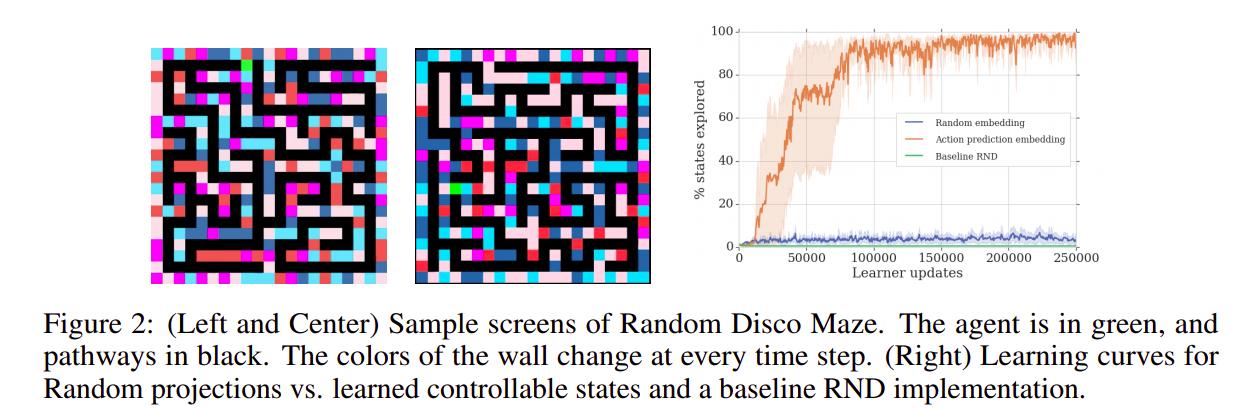
The agent, in green, must navigate the maze, in black. If the agent takes an action that would make it go outside the maze, the experiment stops. At each time step, the colors of the background change, and there is no extrinsic reward.

Results

Fig 2 shows the exploration done by the agent on Random Disco Maze, and this video shows the agent in action.

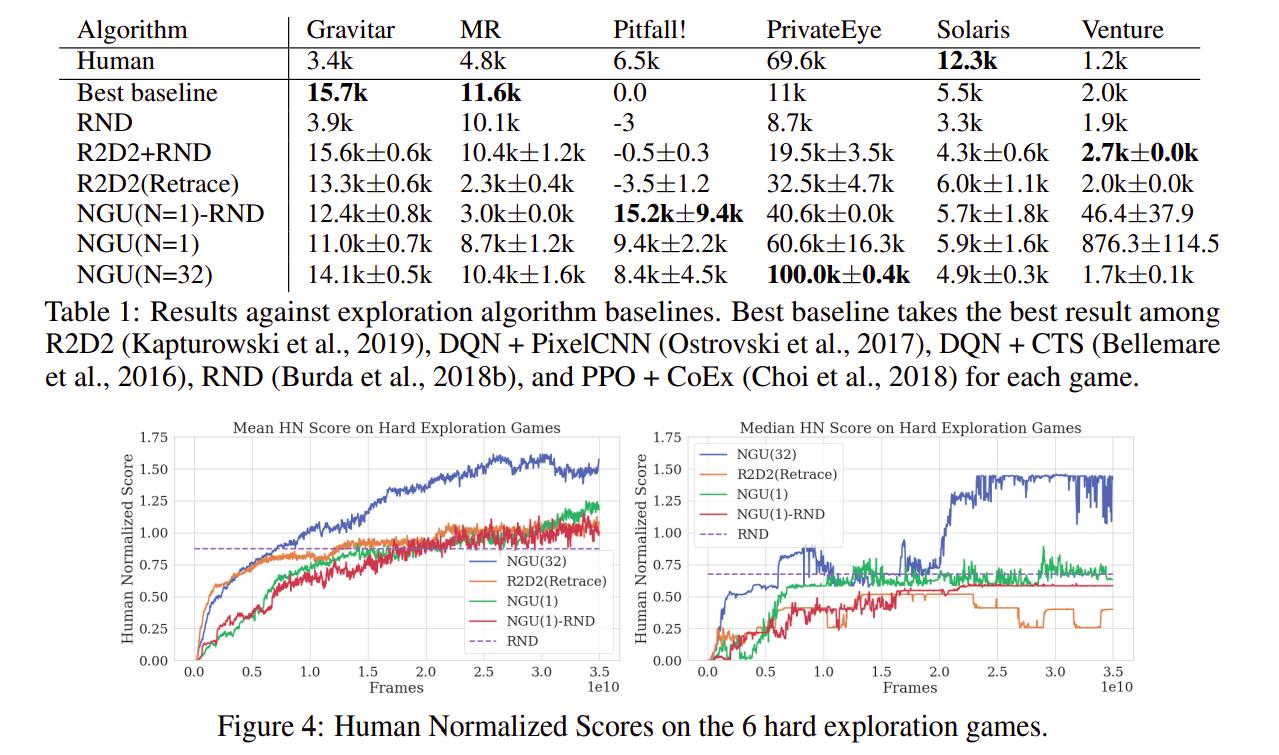
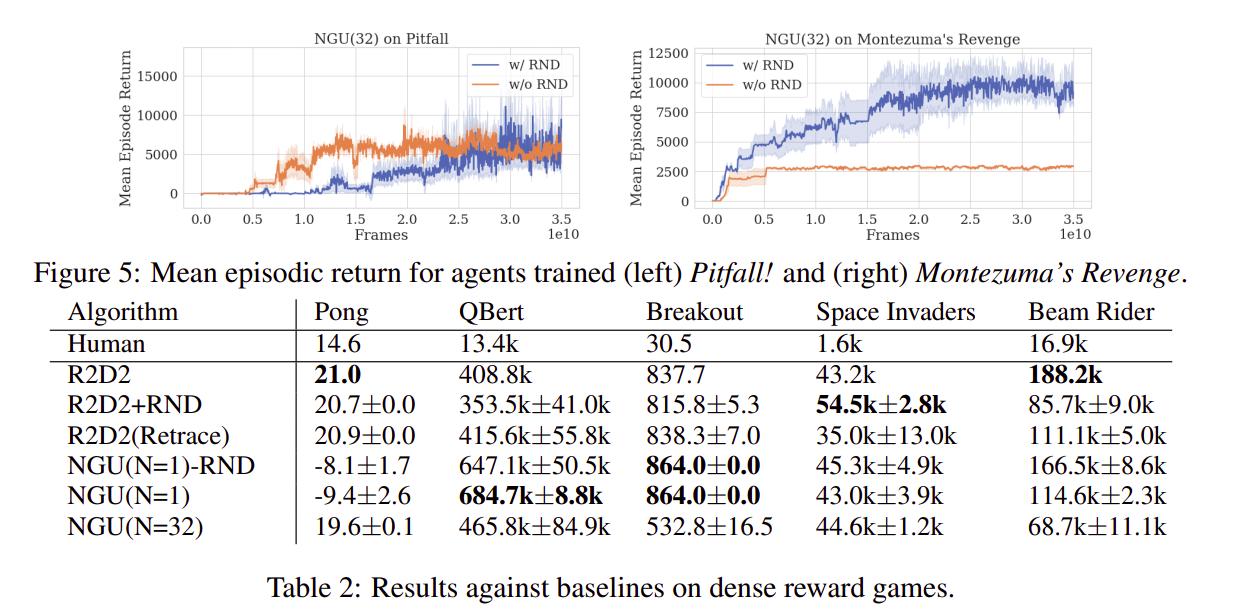
We can see that the agent performs really well on hard-exploration games. Videos of the trained policies are available here: https://sites.google.com/view/nguiclr2020

Results on all Atari 57 games: The proposed method achieves an overall median score of 1354.4%, compared to 95% for Nature DQN baseline, 191.8% for IMPALA, 1920.6% for R2D2, and 1451.8% for R2D2 using retrace loss. […] Even though its overall median score is lower than R2D2, NGU maintains good performance on all games, performing above human level on 51 out of the 57 games. This also shows further confirmation that the learned exploitative mixture is still able to focus on maximizing the score of the game, making the algorithm able to obtain great performance across all games.

Conclusions

The proposed agent is able to achieve high scores in all Atari hard-exploration games as well as achieving high scores on almost all Atari games. It is the first agent to achieve non-zero reward on Pitfall! without relying on human demonstrations or feature hand-crafting.

Remarks

• The results are really really impressive
• As usual, the authors also employ a variety of code-level optimizations and other enhancements that are not part of the contributions. See the appendix for more information.
• I would guess that my interpretation of the results of R2D2 was wrong, because it allows the agent to perform really well
• This agent, NGU, is the base for DeepMind’s Agent 57⁴

References

Poster session at ICLR: https://iclr.cc/virtual_2020/poster_Sye57xStvB.html