Highlights

The authors are working on data that has different domain and different classes and their goal is to disentangle the domain representation from the classes representation. To do so, they built upon the paper Learning Latent Subspaces in Variational Autoencoders.

Methods

To do so, the authors learn 3 latent spaces (as opposed to 1 for a normal VAE) :

• \(z_d\) the domain latent space;
• \(z_y\) the class latent space.
• \(z_x\) the residual latent space;

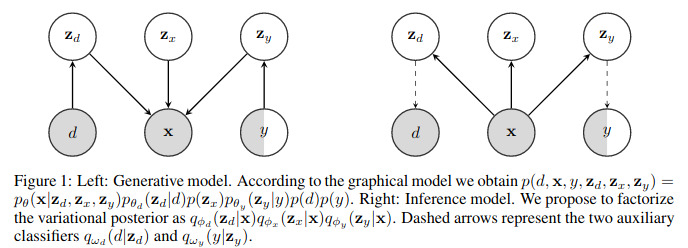
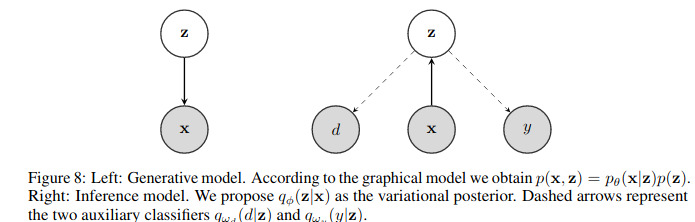
Since the goal is to represent the joint distribution \(p(x,y,d,z_d,z_x,z_y)\) and that the random variables are conditionally related, they provide in Figure 1 a graphical representation of the generative and inference models.

Since the exact inference of \(p(x\mid z_d,z_x,z_y)\) is intractable, they use a variational inference framework (i.e. a VAE) with 3 separate encoders

• \(q(z_d\mid x)\);
• \(q(z_x\mid x)\);
• \(q(z_y\mid x)\);

that serve as variational posteriors. The resulting loss for the 3 subspace-VAE is as follows

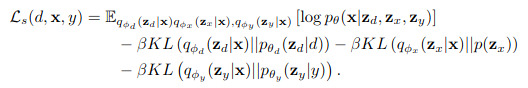
where \(\beta\) has the same disentangling purpose than for \(\beta\)-VAE. Since the graphical model implies the learning of the following two functions

• \(q(d\mid z_d)\);
• \(q(y\mid z_y)\);

they do so via two adversarial neural networks. As such, the resulting Diva loss is

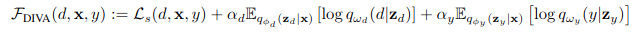
Results

They tested their method on the rotated MNIST dataset: a dataset which contains 6 rotated domains. The visualization of the 3 latent spaces are shown in Figure 2.

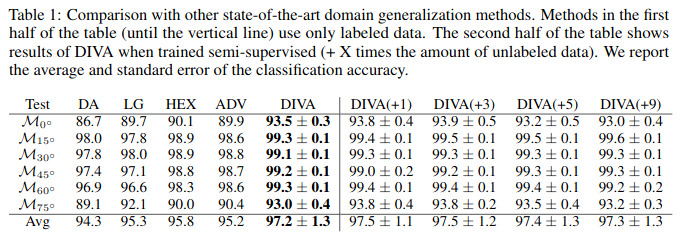
The authors also report good classification accuracies compared to other domain adaptation methods:

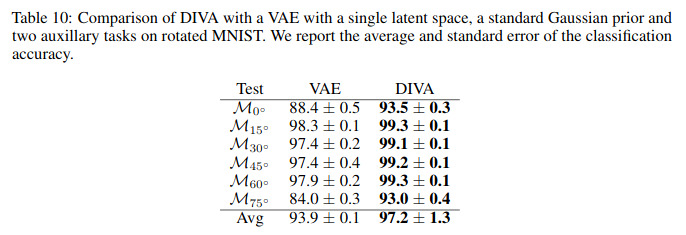
The authors also compared against a single latent space with two adversarial neural networks as shown in Figure 8. Results are reported in Table 10.

Code is available here: https://github.com/AMLab-Amsterdam/DIVA