Highlights

• Novel Conditional Subspace VAE (CSVAE), that learns a low-dimensional latent subspace associated with each label
• The aim of the CSVAE model is twofold:
  • Learn higher-dimensional latent features correlated with binary labels in the data.
  • Represent these features using a subspace that is easy to interpret and manipulate when generating or modifying data.

Introduction

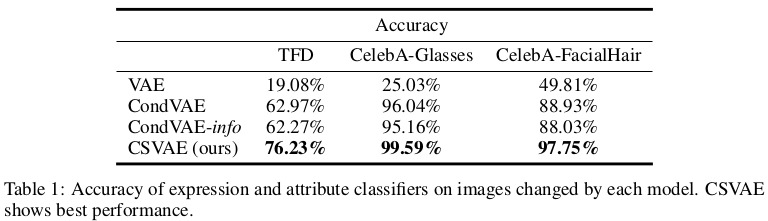
The closest previous work that attempted to remove information correlated with the conditioned label is Conditional VAE with Information Factorization (CondVAE-info), whose objective function is given below:

\[\max_\phi \min_\psi L(r_\psi(q_\phi(z|x)), y)\]

where \(r_{\psi}(z)\) is an additional network trained to predict \(y\) from \(z\). However, the authors claim that the fact that the decoder relies on the one-dimensional variable \(y\) to reconstruct the data is suboptimal, hence the motivation for the CSVAE.

Methods

Suppose we are given a dataset \(D\) of elements \((x, y)\) with \(x \in \mathbb{R}^n\) and \(y \in Y = \{0, 1\}\) representing \(k\) features of \(x\). Let \(H = Z \times W = Z \times \prod_{i=1}^{k} W_i\) denote a probability space which will be the latent space of our model. The goal of the CSVAE is to learn a latent representation of our data which encodes all the information related to feature \(i\) labelled by \(y_i\) exactly in the subspace \(W_i\).

The authors achieve this goal by maximizing a form of variational lower bound on the marginal log likelihood of the model, along with minimizing the mutual information between \(Z\) and \(Y\). Just like in the CondVAE-info, minimizing the mutual information is done with an adversarial network trying to predict \(Y\) from \(Z\).

The detailed explanation of the objective functions is quite long, and should be read in the full paper. To better understand the role of each variable (and the notation used later on) suffice to say that this is how the authors decompose the joint-likelihood:

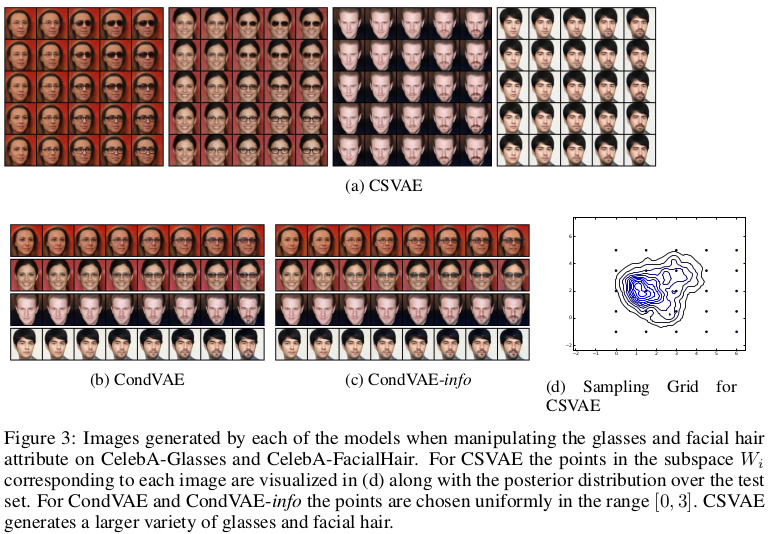
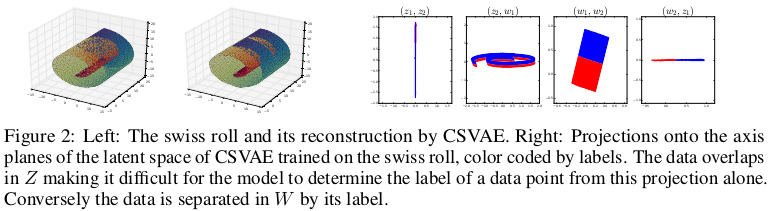
\[\log p_{\theta,\gamma}(x,y,w,z) = \log p_\theta(x|w,z) + \log p(z) + \log p_\gamma(w|y) + \log p(y)\]

An example of what the method can achieve on the swiss roll is shown in Figure 2.

Encoding in subspaces

To project the data in the latent subspaces, the authors seem to use a distinct encoder for each subspace, meaning distinct encoders for each:

• label, in case of binary label, or
• label value, in case of multi-label that should be one-hot encoded (like the TFD referenced later).

For arbitrary fixed choices \(\mu_1,\sigma_1,\mu_2,\sigma_2\), for each \(i=1,\dots,k\) the authors state:

\[p(w_i|y_i=1) = \mathcal{N}(\mu_1,\sigma_1)\] \[p(w_i|y_i=0) = \mathcal{N}(\mu_2,\sigma_2)\]

The authors also mention that they always chose \(W_i=\mathbb{R}_2\) for all \(i\). The choice is arbitrary, but it helps when visualizing the distribution of the data in the latent subspace.

Attribute manipulation

The authors define an attribute switching function \(G_{i,j}\) to change the label of \(x \in X\) from \(i\) to \(j\).

As reference, we could define \(G_{i,j}\) in the following manner for a traditional VAE:

For each \(i = 1,\dots,k\) let \(S_i\) be the set of \((x,y) \in D\) with \(y_i=1\). Let \(m_i\) be the mean of the elements of \(S_i\) encoded in the latent space, that is \(\mathbb{E}_{S_i}[\mu_\phi(x)]\). We can define:

\[G_{i,j}(x) = \mu_\theta(\mu_\phi(x) - m_i + m_j)\]

For the CSVAE, the definition of \(G_{i,j}\) is now as follows:

Let \(p = (p_1,\dots, p_k) \in \prod_{i=1}^k W_i\) be any vector with \(p_l = \vec{0}\) for \(l \neq j\). For \((x,y) \in D\) we can define:

\[G_{i,j}(x,p) = \mu_\theta(\mu_{\phi_1}(x), p)\]

Data

As for real experiments, the model was tested on two different faces datasets. First, the Toronto Faces Dataset, consisting of approximately 120,000 grayscale face images partially labelled with expressions and identity. Second, the CelebA dataset of approximately 200,000 images of celebrity faces with 40 labelled attributes. In the latter case, the authors filtered the data into two separate datasets which focus on a particular attribute of interest.

Results