Highlights

• Modality invariant transformer that provides a self-supervised signal and is used to predict future anatomical factors from current ones
• State of the art performance compared to semi-supervised segmentation made by SDNet (from a previous paper by the same group¹)
• Preliminary results of cardiac temporal synthesis

Introduction

The authors state that temporal correlations use in (cardiac) medical imaging has been limited to an additional signal/supervision for segmentation tasks. They propose to use spatiotemporal dynamics to improve disentangled representations.

Methods

Spatial Decomposition Network (SDNet)

The SDNet framework is an attempt to decouple anatomical factors from their appearance towards more explainable representations.

The SDNet can be seen as an autoencoder that learns multiple subspaces, namely:

• \(s = f_A (x)\): a multi-channel output of binary maps, representing the anatomical components
• \(z = f_M (x)\): the \(Q(z \vert X)\) multivariate Gaussian as in a standard VAE, representing the modality components

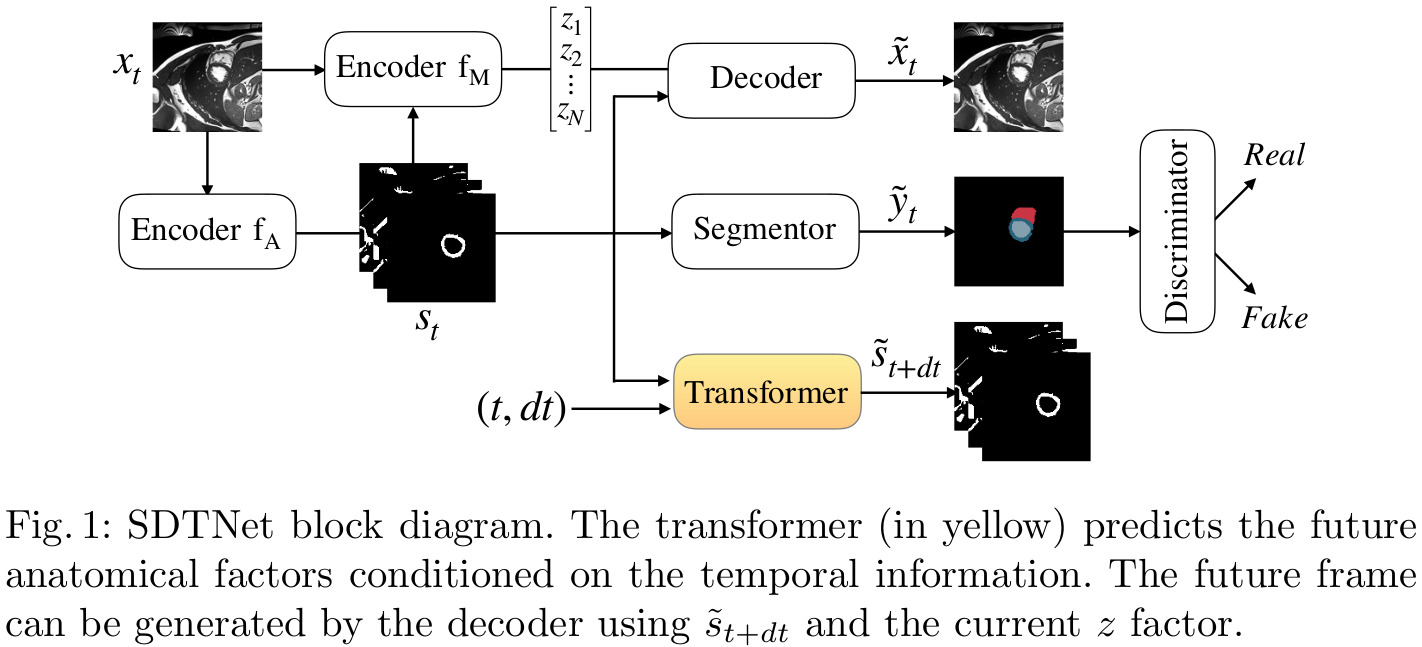
Spatial Decomposition and Transformation Network (SDTNet)

The goal of this architecture is to learn anatomical factors that are both spatially and temporally consistent. To this end, the authors add a UNet to act as a transformer and predict future anatomical components from current ones, conditioned on temporal information. These deformed anatomical factors, together with the fixed modality factors \(z_t\), should be enough to reconstruct the input from a future time point.

Figure 1 illustrates the additions brought by SDTNet (in yellow) to the base SDNet framework.

The overall loss function is a weighted sum (determined empirically) of:

• \(L_S = L_{DICE}(y,\tilde{y}) + 0.1 \cdot L_{CE}(y,\tilde{y})\), the supervised segmentation task cost;
• \(L_{US} = |\tilde{x} - x| + \lambda_{KL} \cdot D_{KL}[Q(z|X) \| N(0,I)] - MI(\tilde{x},z)\), the cost of the unsupervised encoding task;
• \(L_{ADV}\) is the adversarial loss of a Least-Squares GAN to discriminate ground truth from predicted segmentations;
• \(L_{TR}\) is the self-supervised signal, represented as the Dice loss between \(\tilde{s}_{t+dt}\) and \(s_{t+dt}\).

The authors optimized the model using the Exponential Moving Average (EMA), claiming that it detects wider and more generalizable minima.

Data

The experiments were performed on a 3-fold cross-validation split of ACDC’s training set. To obtain consistent temporal transformations, the authors split the sequences in two halves:

• The ED-ES interval were left as is;
• The frames from ES to the end of the cardiac cycle were reversed in temporal order to mimic the cardiac contraction.

Results

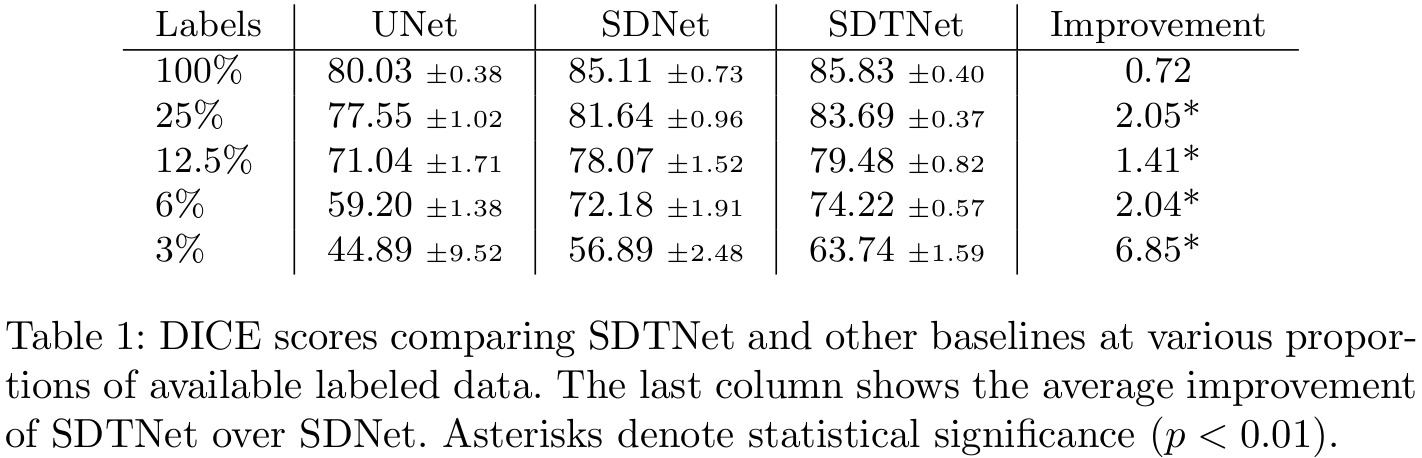
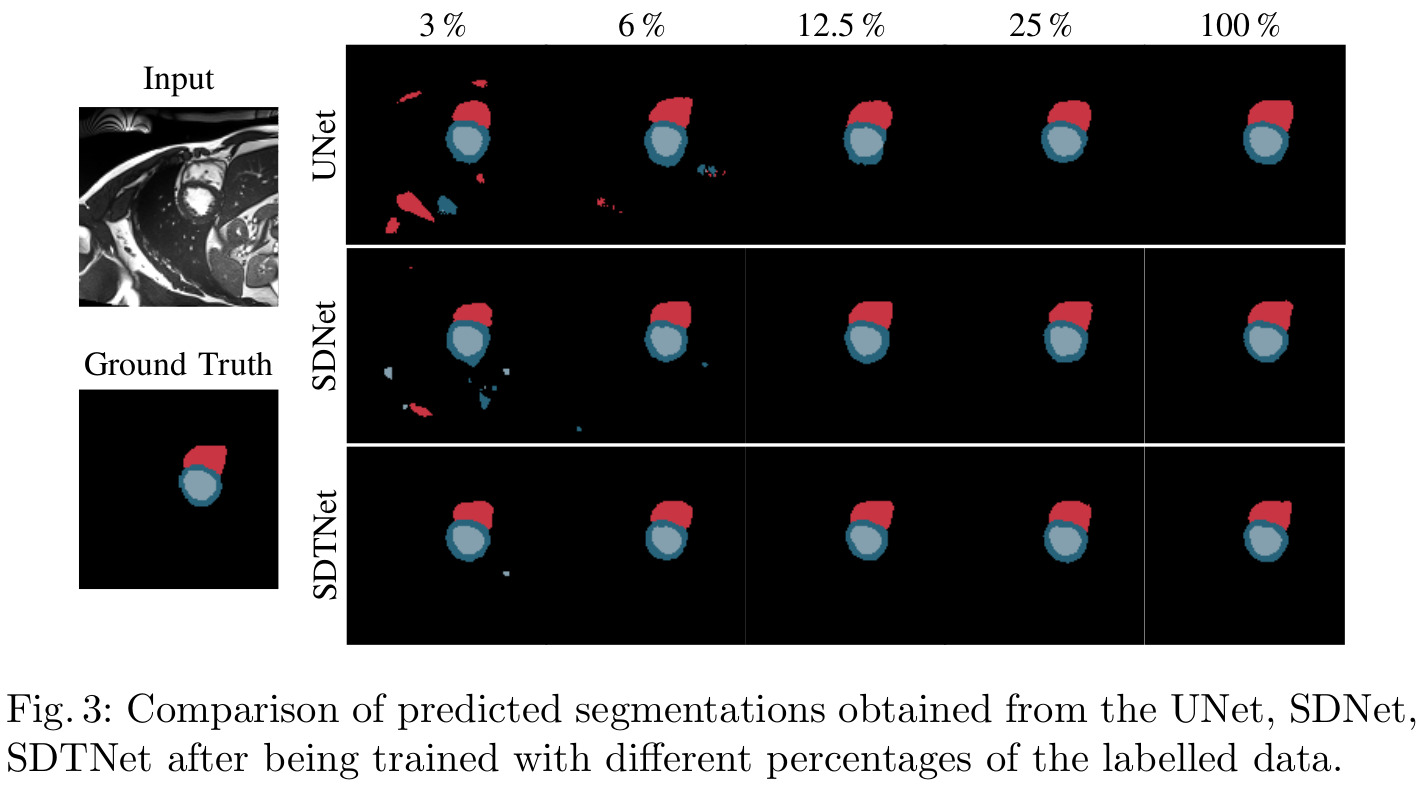
Remarks

• Although the authors mention temporal consistency often in relation to their transformer, no evaluation of the temporal coherence, either quantitative or simply qualitative, is provided.

References