Lottery managers hate him! This DeepMind researcher found one weird trick for rigging the lottery.

In this paper from DeepMind folks, the authors introduce a “dense-sparse-dense”-like method for reducing the number of useless weights in a network. In other words, the goal is to have “winning tickets” for every remaining weight. The Lottery metaphor comes from The Lottery Ticket Hypothesis.

Method

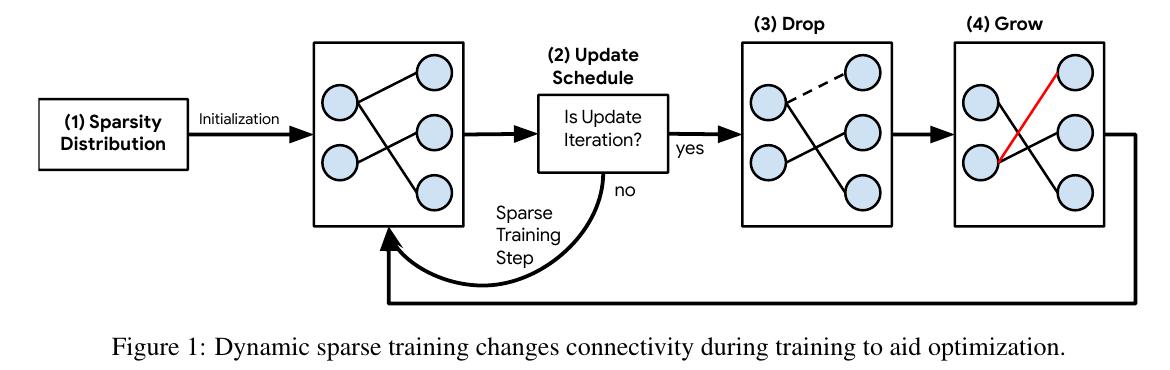
Sparsity distribution. The authors propose three approaches for distributing sparsity across the layers. The most simple is “uniform”, where every layer has the same sparsity. The two other methods take into account the number of connections: bigger layers are pruned more than small layers. The third and best performing approach takes into account the convolutional kernel size.
Update schedule. Sparsification (Drop operation) happens at a certain frequency during training. At each drop operation, the sparsity can change. The authors define a function taking as input the index of the step, and returning a sparsity in the range [0, 1].
Drop criterion. During a drop operation, the weights with the lowest magnitude are dropped. The number of weights dropped is determined in (2).
Grow criterion. During a grow operation, the weights receiving the highest gradient will be re-added. The number grown connections is the same as the dropped in (3). The grown connections are initialized at zero.

An interesting feature of this approach is that pruned filters can be removed from the graph. The total number of connections (including those currently pruned) can be larger than what the GPU memory allows. In practice this only works for filter-wise sparsity.

Results

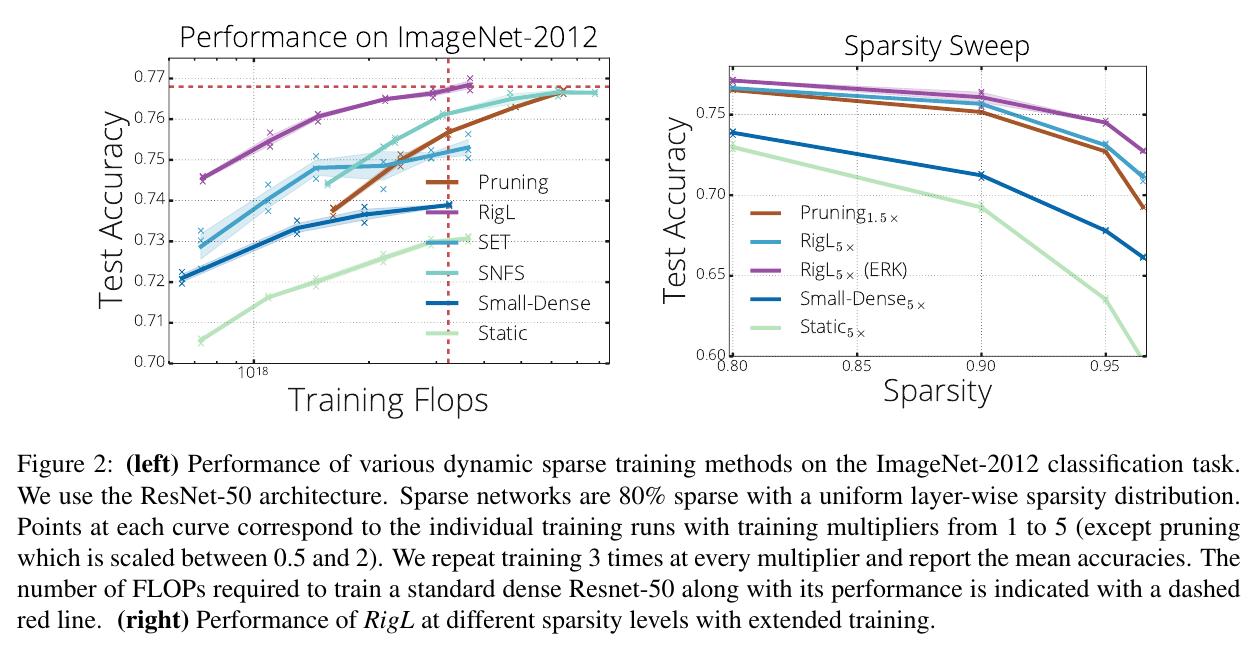
Authors claim their method is SotA for sparsity and FLOPs. The improvement is not mind-blowing, but it seems significant.

Conclusion

The main novelty of this paper is its “grow criterion”. It is a good idea, that could take off in the “network pruning / architecture search” niche.