Activation functions play a critical role in deep learning, influencing how models learn and generalize. Below is a description of the relationships between several important activation functions: ReLU, ELU, GELU, GLU, SiLU, Swish, ReGLU, GEGLU, and SwiGLU.

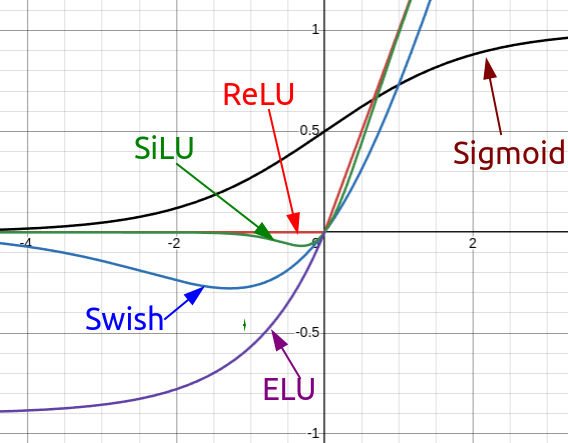
1. ReLU (Rectified Linear Unit)

ReLU is one of the most commonly used activation functions in neural networks. It is defined as:

\[\text{ReLU}(x) = \max(0, x)\]

If \(x\) comes from a previous layer, we have \(x=Wx^-+b\) where \(x^-\) is the output of the layer before.

2. ELU (Exponential Linear Unit)

ELU is an extension of ReLU that introduces smoothness for negative inputs, defined as:

\[\text{ELU}(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha(\exp(x) - 1) & \text{if } x < 0 \end{cases}\]

3. GELU (Gaussian Error Linear Unit)

GELU is a more sophisticated activation function that models the neuron activation probabilistically:

\[\text{GELU}(x) = x \cdot \Phi(x)\]

where \(\Phi(x)\) is the cumulative distribution function of the Gaussian distribution.

4. SiLU (Sigmoid Linear Unit)

SiLU is a simple approximation of ReLU but without any discontinuity of the first derivative:

\[\text{SiLU}(x) = x \cdot \sigma(x)\]

where \(\sigma(x)\) is the sigmoid function.

5. Swish

Swish is a simple generalization of SiLU

\[\text{Swish}(x) = x\sigma(\beta x)\]

where \(\beta\) is learnable. When \(\beta=1\), Swish becomes SiLU.

6. GLU (Gated Linear Unit)

GLU introduces a gating mechanism where the output of a linear transformation is modulated by a gate:

\[\text{GLU}(x) = x_1 \cdot \sigma(x_2)\]

where \(x_1 = Wx^-+b\) and \(x_2 = Vx^-+c\) are different linear transformations of the input \(x\).

7. ReGLU (Rectified Gated Linear Unit)

ReGLU is a variant of GLU that uses ReLU instead of the sigmoid function as the gating mechanism:

\[\text{ReGLU}(x) = x_1 \cdot \text{ReLU}(x_2)\]

8. GEGLU (Gaussian Error Gated Linear Unit)

GEGLU is another variant of GLU that uses GELU instead of the sigmoid function:

\[\text{GEGLU}(x) = x_1 \cdot \text{GELU}(x_2)\]

9. SwiGLU (Swish-Gated Linear Unit)

SwiGLU replaces the gating mechanism in GLU with the Swish activation function:

\[\text{SwiGLU}(x) = x_1 \cdot \text{Swish}(x_2)\]