Highlights

• SAC is the baseline model-free RL algorithm since 2018
• REDQ improves of SAC by using an ensemble of critics and a UTD ratio » 1
• DroQ improves on REDQ to use a smaller ensemble of critics, includes dropout
• CrossQ improves on DroQ to use a single critic, no target network and includes batch norm

Introduction

Since its proposal in 2018, Soft Actor Critic (SAC) algorithms¹² have become the standard for online model-free reinforcement learning (RL). It’s “maximum-entropy” framework proved very useful to balance exploration and exploitation while being very simple to implement, making use of the expressivity of Q functions instead value functions like PPO³, for example.

Through the years, some improvements over SAC have been suggested, mostly in the hope of improving the data efficiency of learning agents.

Soft-Actor Critic

SAC presumes that there is more than one optimal solution to a given problem and that therefore, we would like to prevent the optimal policy from converging to a single one. Moreover, a policy with a high entropy will explore more and may prevent it from converging to a bad policy early on.

To do so, the standard RL objective is modified so as to become:

\[\pi^* = \arg\max_{\pi} \mathbb{E}_{(s,a)~\sim\pi)} \big[\sum_{t=0}^\infty \gamma^t r(s_t, a_t) + \alpha \mathbb{H}(\pi(\cdot | s_t))\big]\]

The Q-function becomes

\[Q^\pi(s,a) = \mathbb{E}_{(s,a)~\sim\pi)} \big[\sum_{t=0}^\infty \gamma^t r(s_t, a_t) + \alpha \sum_{t=1}^\infty \gamma^t \mathbb{H}(\pi( \cdot | s_t)) \big | s_0 = s, a_0 = a \big],\]

therefore giving an implicit reward bonus proportional to the policy’s entropy at each timestep.

SAC uses two critics to fight overestimation by using the minimum of the two predictions. The critic loss can be formulated as

\[L(\theta_i, \mathcal{D}) = \mathbb{E}_{(s,a,s',d)\sim\mathcal{D}} [(Q_{\theta_i}(s,a) - y(s,a,s',d))^2]\]

with

\[y(r,s,a,s',d) = r(s,a) + \gamma (1-d) \big[\min_{j=1,2} Q_{\bar{\theta_j}}(s',\bar{a}', s') - \alpha \log \pi(\bar{a}' | s')\big], \; \bar{a}' \sim \pi(\cdot | s'),\]

and \(Q_\bar{\theta}\) the target critics.

REDQ

After SAC, a few algorithms have brought forth the concept of Update to Data ratio (UTD). Essentially, SAC and other off-policy algorithms typically acquire a transition, put it in the replay buffer, sample it randomly, update the agent and then acquire another transition. This amounts to a UTD of 1. A few algorithms, mostly model-based RL, argue this is inefficient and agents can benefit from sampling the buffer and updating the agent multiple times (twice, ten or fourty times) between transition acquisitions, speeding up learning.

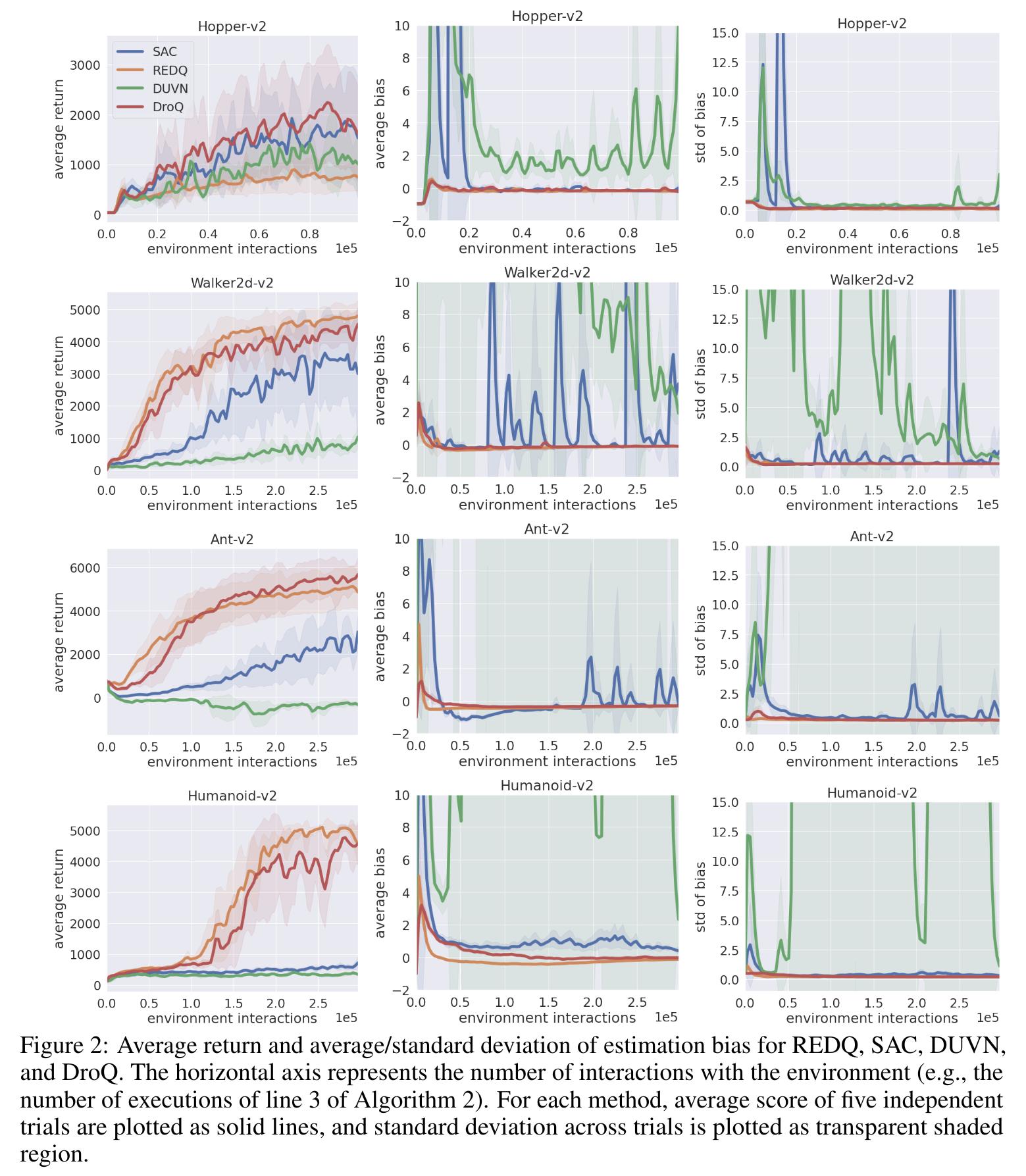
Randomized Ensembled Double Q-Learning⁴ (REDQ) improves upon SAC by employing a UTD around 20. However, this alone would lead to a high bias in the Q function and a high variance in the bias as well. The authors then propose to include an ensemble of critics (10) but only use a random sample when performing the update (2).

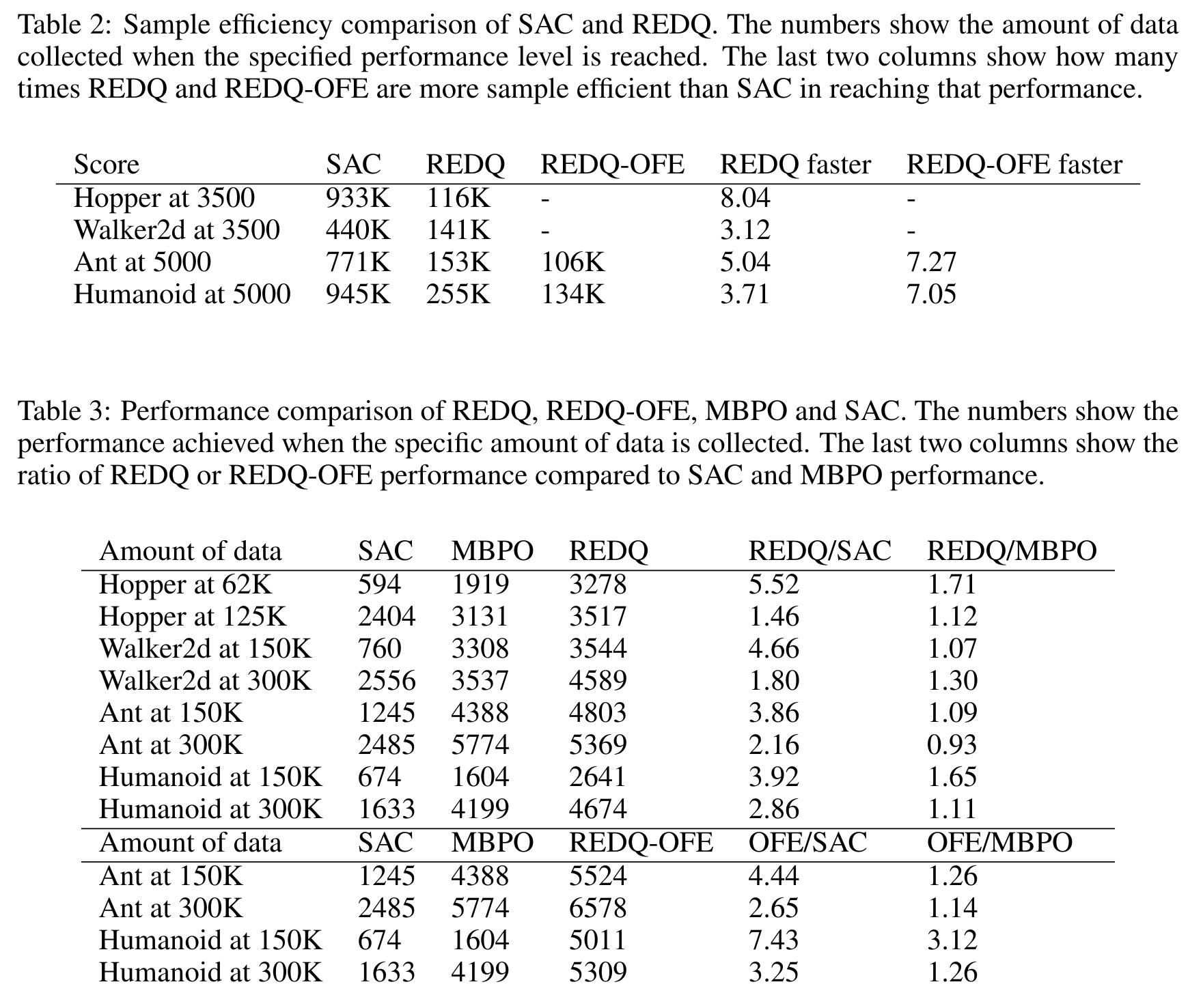
DroQ

The large ensemble of critics used by REDQ has its downsides: updating \(N\) critics at each update, coupled with a high UTD ratio, is computationally expensive. The authors of ⁵ argue that REDQ injects the critics’ uncertainty into the target via its random sampling of its ensemble.

To keep this uncertainty without the high cost of many critics, Dropout Q-functions (DroQ) is ⁵ proposed to instead use a small ensemble of critics (2) with dropout and layer normalization.

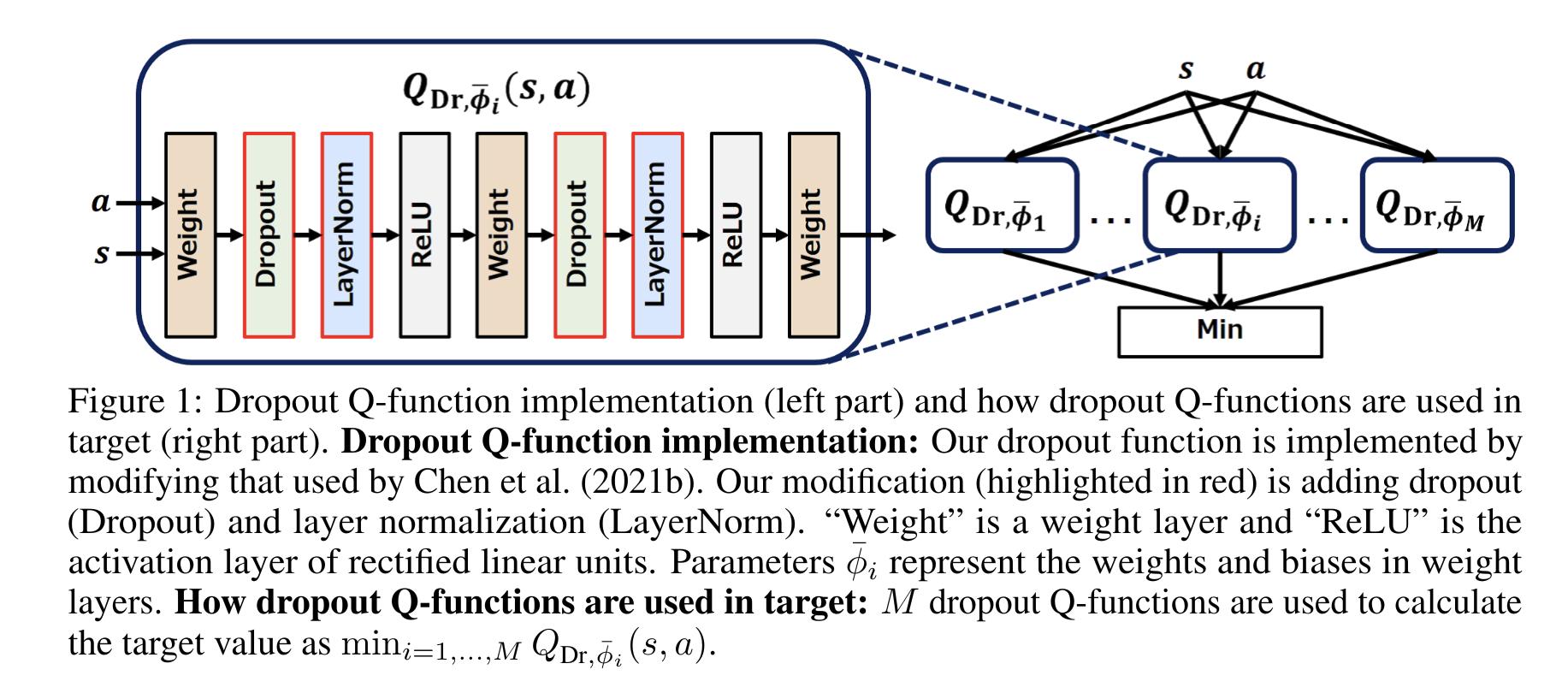
As a baseline method, the authors (re)introduce Double Uncertainty Value Network (DUVN) by using only one critic without layer norm.

CrossQ

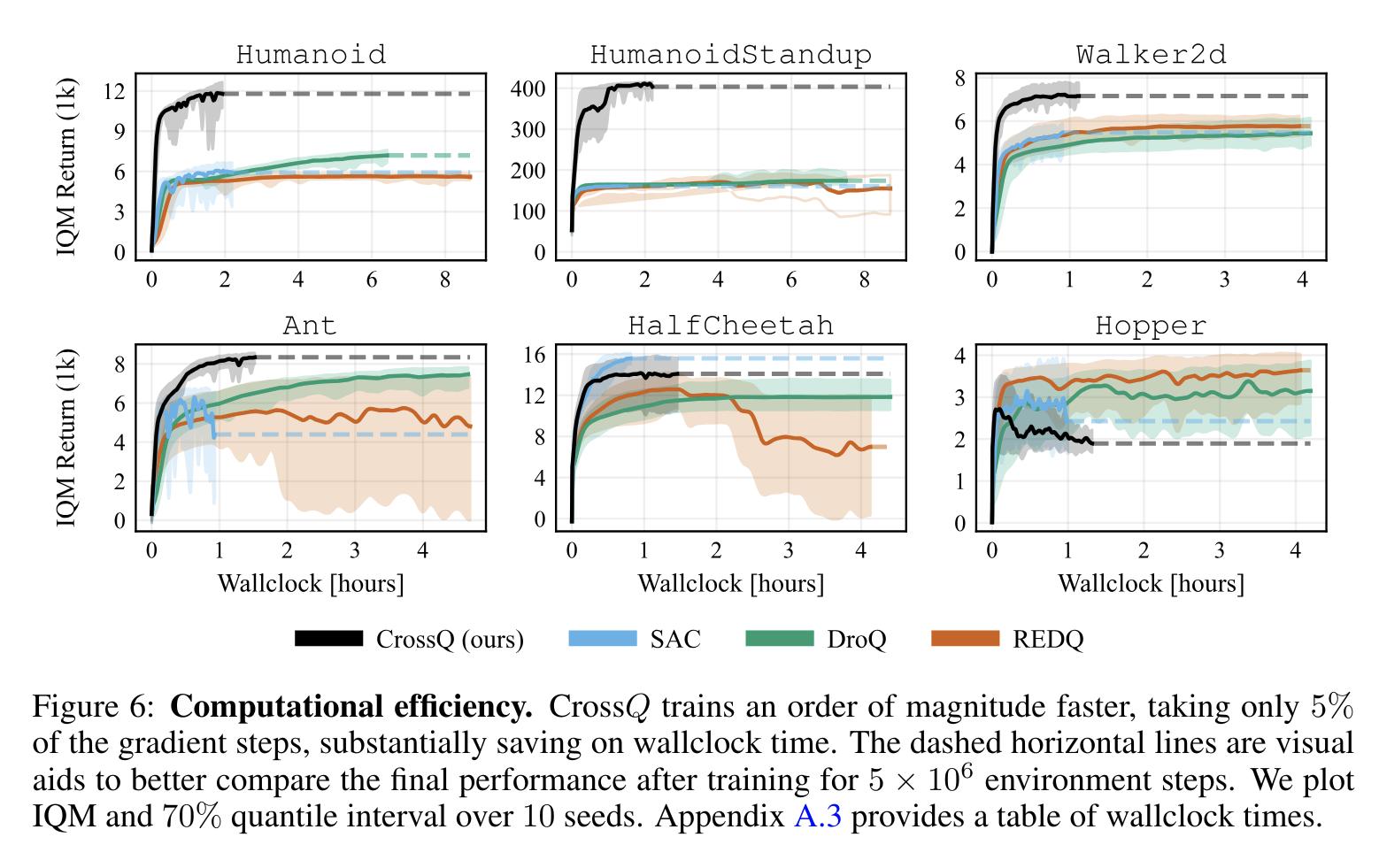
While a high UTD ratio is appealing as it reduces the bias and its variance, it comes at great computational costs. To improve even more the computational efficiency of maximum entropy off-policy RL, CrossQ (as it crosses out many complexities added over the years) ⁶ is introduced by reducing the UTD to 1. To increase stability, Batch ReNormalization is added to the agents.

The critic loss uses both \((s,a)\) and \((s', a')\), where \(a' \sim \pi(s')\) while \(s, a, s'\) come from the replay buffer. However, using batch norm naively, \((s', a')\) would be out of distribution for the batch norm statistics of the target critic given that its weights are updated from polyak averaging of the actual critic. Therefore, the authors propose to forgo the target network and concatenate \((s, a)\) and \((s', a')\) when estimating the Q values so that the Batch Norm statistics are a 50/50 mix of their respective distributions [sic].

References