Highlights

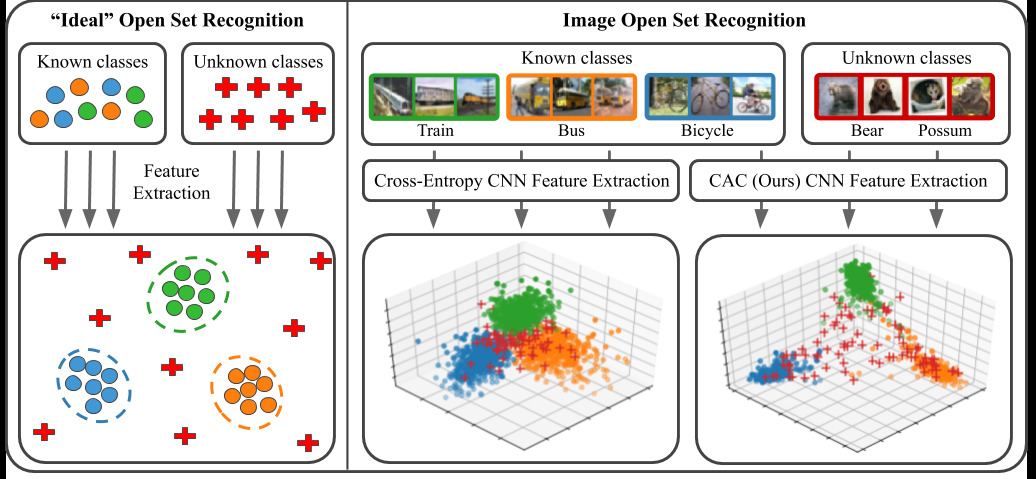
This paper proposes a new loss called the CAC (Class anchor clustering) loss tailored to open-set recognition problems. That loss “encourages known class training data to cluster tightly around class-specific centers in logit space”. Open set recognition problems are those for which object classes observed at test time were unknown during training. The loss builds upon two important concepts, namely the notion of class anchor and softmin function.

The main takeaway

The loss function

The building blocks of the proposed method are as follows:

  • a neural network \(f\) that outputs a logit vector \(\vec z = f(x)\)
  • a set of class anchors \((\vec c_1,...,\vec c_N)\) with the same number of dimensions than \(\vec z\)
  • a distance layer which computes the distance between \(\vec z\) and each anchor : \(\mathbf{d} = (\|\vec z-\vec c_1\|_2,\) … \(,\|\vec z-\vec c_N\|_2 )\)

The loss is based upon the notion of a softmin function which is “the opposite of softmax as it assigns a large value (≈ 1) to the smallest value of the input vector” :

\[softmin(\mathbf{d})_i = \frac{e^{-d_i}}{\sum e^{-d_k}}\]

By taking the \(-\log(.)\) of that function (just like a cross entropy) one gets the following loss:

\[L_T(x,y) = \log\left( 1 + \sum_{j\neq y} e^{d_y-d_j}\right)\]

whose effect is to maximize the margin between the correct and the incorrect classes. To explicitly lower the distance to the correct class center, they use a second loss function :

\[L_{A}(x,y) = \| f(x)-c_y\|_2.\]

The overall loss function is:

\[L_{CAC} = L_T(x,y) + L_{A}(x,y)\]

The class anchor

The anchored class center \(\vec c_i\) are scaled one-hot vectors:

\[(\vec c_1, ..., \vec c_N) = (\alpha.\vec e_1, ..., \alpha.\vec e_N)\]

where \(\alpha\) is a hyperparameter and \(\vec e_i\) is the i-th one-hot vector.

Results

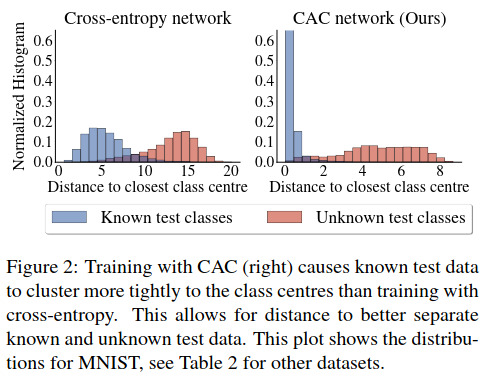
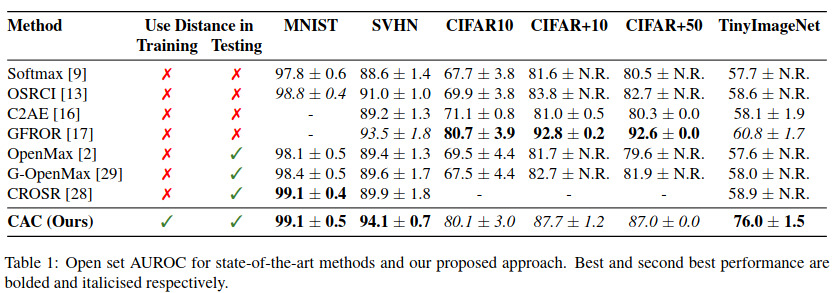
Several results are presented, maybe the most interesting ones are the ones in Figure 2 where we see a better separation between the known and the unknown classes and Table 1 for the AUROC scores on 6 different datasets obtained against 7 competing methods.

References