Escaping the Big Data Paradigm with Compact Transformers
Highlights
Quick review of a nice method which may very well democratize the use of transformer networks applied to image classification tasks. While recognizing the spectacular performances of transformer networks (especially the seminal ViT) on large (imageNet), very large (ImageNet-21K) and humongous (JFT-300M) datasets, they recall that as the ViT authors mentioned : Transformers lack some of the inductive biases inherent to CNNs, such as translation equivariance and locality, and therefore do not generalize well when trained on insufficient amounts of data. Said otherwise, tranformers are data hungry. They are also huge models with, for ViT, approximately 86 million learnable parameters. For these reasons, transformer networks are ill-suited for most context of use.
In this paper, the authors propose a Compact Vision Transformer as well as a Compact Convolutional Transformer whose goal is to pull transformers out of the “Big Data” trap. Both methods are illustrated in Figure 3.
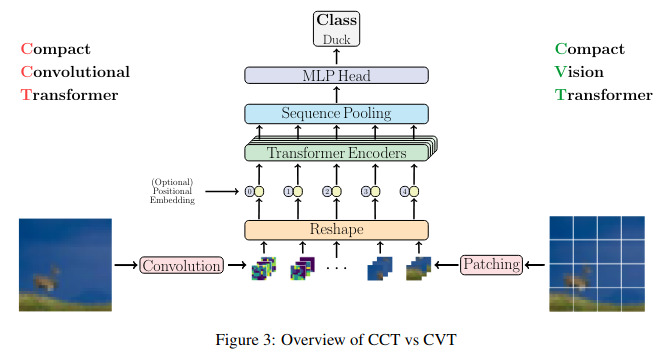
Methods
The main difference between the original ViT network and the proposed CVT and CCT networks are illustrated in the following figure. Note that the Transformer Encoder is the same as the one originally proposed by Dosovitskiy et al.
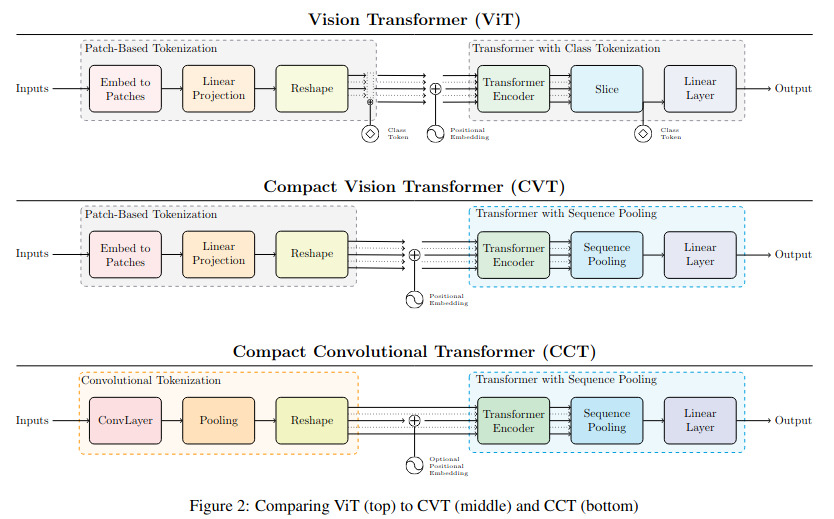
(Dosovitskiy et al’s Vision Transformer (ViT))
Compact Vision Transformer (CVT)
For this model, the patch embedding/tokenization module is the same as for the original ViT. However, the CVT has no class token and instead use a sequence pooling block before the final linear+softmax layer.
When processing one input image, the output \(x_L\) of the transformer encoder is an \(n\times d\) matrix containing \(n\) output vectors of size \(R^d\). While the well-known average pooling would average these vectors together, sequence pooling (also called attention pooling) computes a weighted average. This is done by first computing
\[x'_L = softmax(Wx_L^{T})\]where \(W\in R^{1\times d}\) and thus \(x'_L \in R^{1\times n}\). The resulting pooled vector is computed as
\[z = x'_L x_L \in R^{1\times d}.\]Compact Convolutional Transformer (CCT)
Instead of dealing with patches, the CCT uses convolutions and pooling operations. This is a fairly straight forward operation which may be summarized as
\[x_0 = MaxPool(ReLU(Conv2d(x)))\]where Conv2d has \(d\) filters to recover the same number of embedding dimensions as the CVT. Boom! there you go.
Also, since convolutions are translation invariant, the positional embedding is optional. The same sequence pooling is used at the end.
Results
In their notation, they use the number of encoder layers and the convolutional kernel to characterize their model. For instance, CCT-12/7×2 means that the transformer encoder has 12 layers and the conv tokenization has 2 convolutional blocks with 7×7 convolutions. They follow the same format for other models.
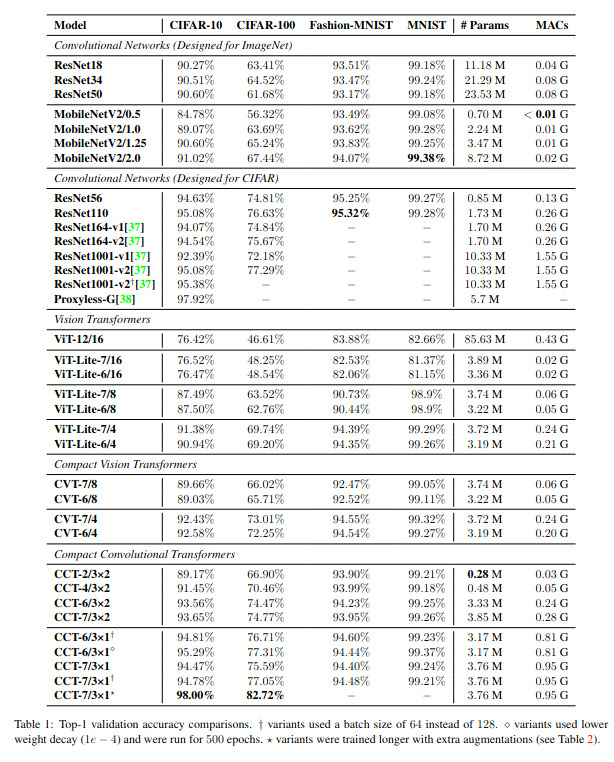
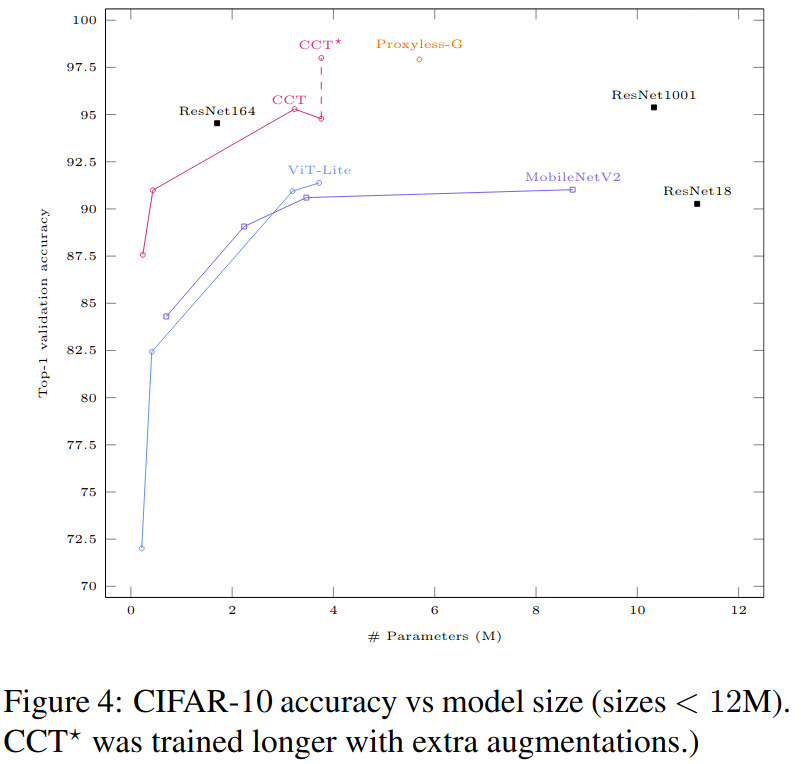
While the authors report all kinds of interesting results, I think that the most explict ones are in Table 1 where CCT with less than 4M parameters get up to 98% accuracy on CIFAR10 and 82.7% accuracy on CIFAR100. Another interesting result is the plot of Fig.4 showing the CIFAR10 accuracy VERSUS the number of parameters. Here again, CCT win. Et voilà!
References
- Nice blog with comprehensive code: https://medium.com/pytorch/training-compact-transformers-from-scratch-in-30-minutes-with-pytorch-ff5c21668ed5