Highlights

• Simple regularization method for image VAEs to enforce invariance to semantics-preserving transformations, applicable to any specific VAE architecture;
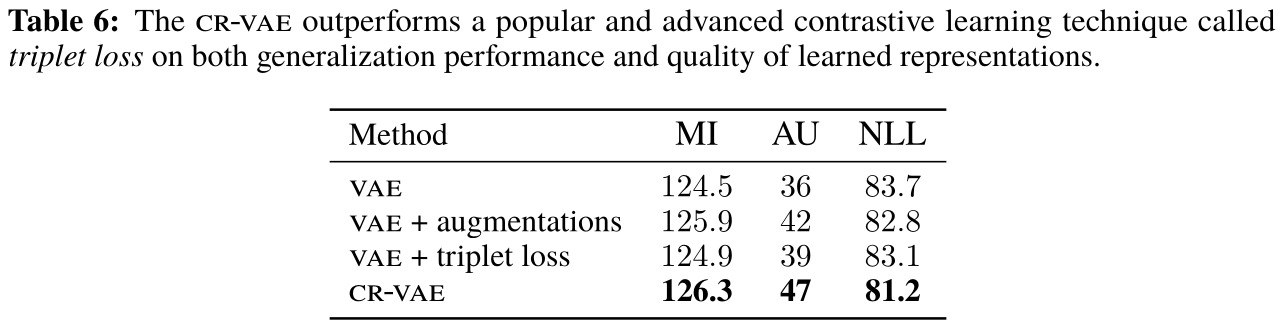
• The proposed method is similar in concept to contrastive learning methods (e.g. triplet loss, NCE), it performs better than the triplet loss in the specific case of image VAEs.

Introduction

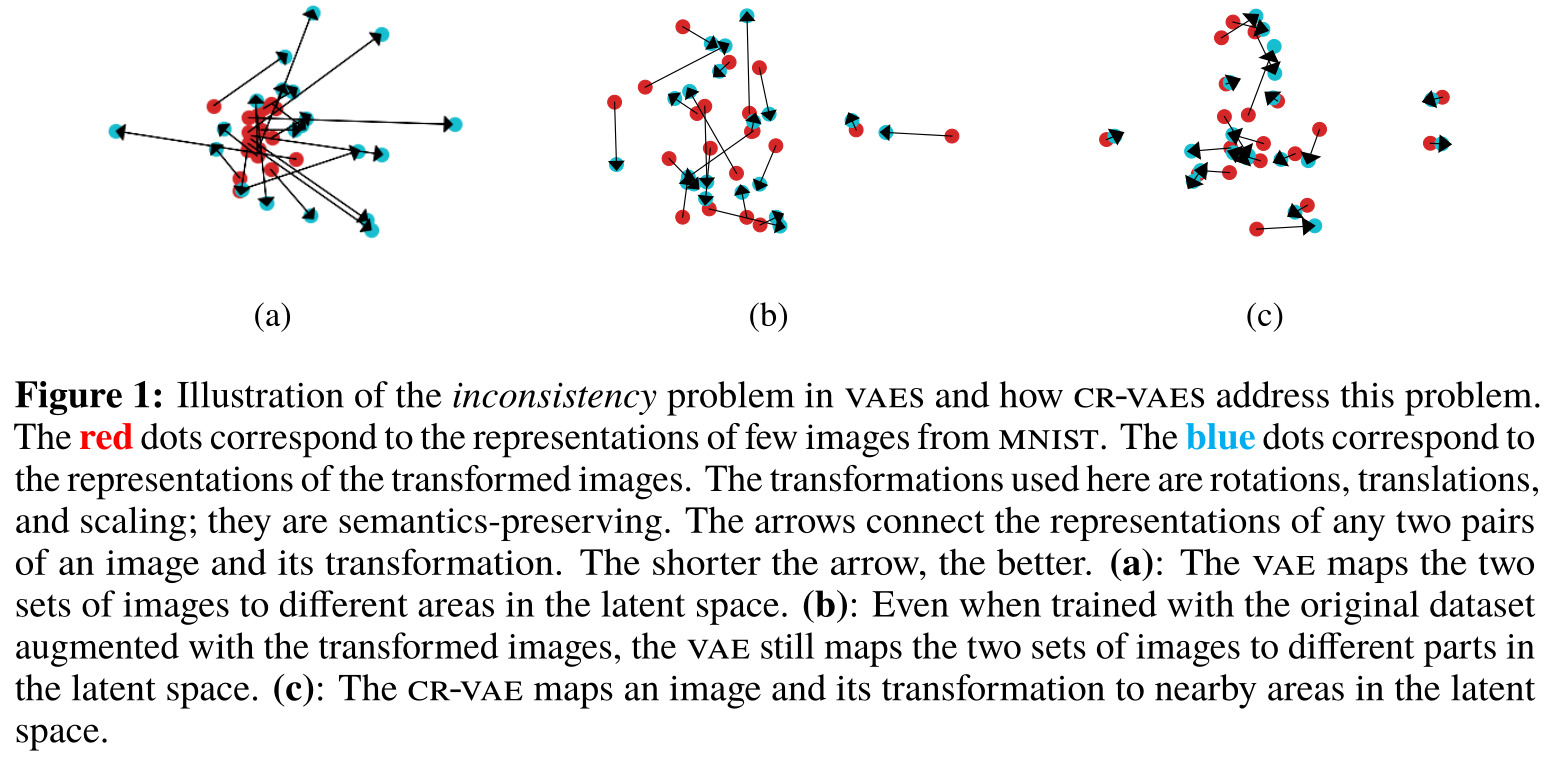
The authors aim to solve what they consider the inconsistency problem in VAEs, which consists of transformations of images that do not affect their semantic content (e.g. translation, rotation, scaling, etc.) being encoded far away from the original images themselves in the latent space (see fig. 1).

The authors argue that while contrastive learning and consistency regularization have been applied to other networks on the logit output, their method is nonetheless novel for applying that concept to the latent space of a VAE.

Methods

Inspired by contrastive learning methods, the authors seek to train a VAE to be invariant to semantics-preserving transformations by adding a regularization term, i.e. the KL divergence, that encourages the posterior distributions of the original image and its transformation to be equal.

The authors define their new objective as:

\[\mathcal{L}_{\text{CR-VAE}}(\mathbf{x}) = \mathcal{L}_{\text{VAE}}(\mathbf{x}) + \mathbb{E}_{(t(\tilde{\mathbf{x}}|\mathbf{x}))}[\mathcal{L}_{\text{VAE}}(\tilde{\mathbf{x}})] - \lambda \cdot \mathcal{R}(\mathbf{x},\phi)\]

where \(\tilde{\mathbf{x}}\) is the result of applying transformation \(t\) to \(\mathbf{x}\), and the regularization term \(\mathcal{R}(\mathbf{x},\phi)\) is:

\[\mathcal{R}(\mathbf{x},\phi) = \mathbb{E}_{(t(\tilde{\mathbf{x}}|\mathbf{x}))}[\text{KL}(q_{\phi}(\mathbf{z}|\tilde{\mathbf{x}}) \| q_{\phi}(\mathbf{z}|\mathbf{x}))]\]

Data

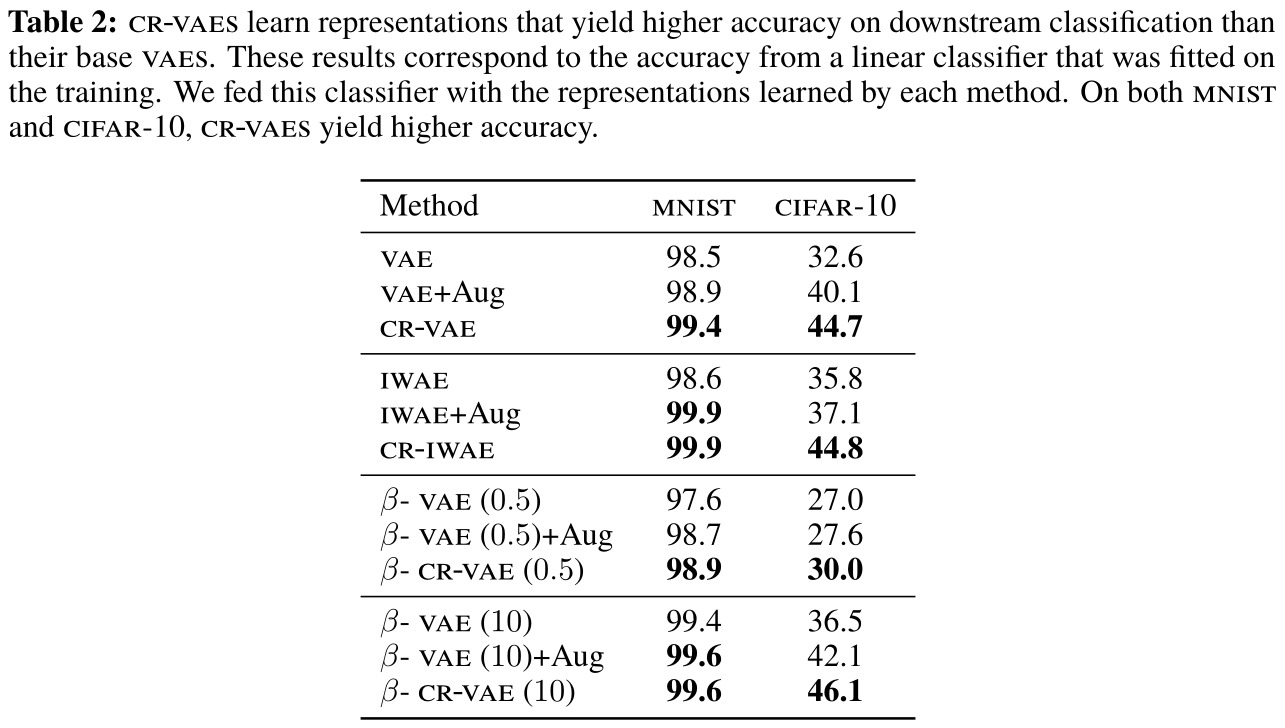
The authors compare their CR-VAE to standards VAE and \(\beta\)-VAE, and a few other SOTA VAE methods. They test the methods on MNIST¹, Omniglot² (handwritten alphabet recognition dataset) and CelebA³.

Results

The authors compare the learned representations by reporting direct measures of the representations (e.g. mutual information) and performance on downstream tasks (e.g. classification accuracy).

The paper presents more results as well as an ablation study, but the results shown below are representative of the trend across the different experiments. The improvements over other VAE methods seem mostly marginal.

References