Highlights

  • Extend the VAE framework to work with heterogeneous, i.e. multi-modal, data by projecting all “channels” to a common latent representation;
  • Use variational dropout to learn sparse representation, which are useful to discover in an unsupervised manner the optimal number of dimensions, i.e. the number of ground truth generative factors.

Introduction

The authors mention previous methods that try to jointly analyze heterogeneous data as:

  • Recognition methods (Partial Least Squares, Canonical Correlation Analysis) that compress the information in a lower dimensional space where constraints are enforced. However, these methods lack generative capabilities;
  • Bayesian CCA a generative formulation of CCA, where “a transformation of a latent variable captures the shared variation between data channels”;
  • VAEs may suffer from interpretability issues, since disentangling the contribution of a single “channel” to the latent representation might not be possible. Since channels are also simply concatenated at the input, the models can only be used when the contains all the channels the models were trained on. Another factor that affects the interpretability of the representations is the lack of a theoretical justification for the choice of the latent space dimension.

Therefore, the authors’ goal is to propose a generative model that relies on an interpretable representation of heterogeneous data.

Methods

Multi-Channel Variational Autoencoder

The authors generalize the VAE by assuming that in a multi-channel scenario the latent representation associated to each channel must match a common target distribution. They impose a constraint on the latent representations in an information theoretical sense, where each latent representation is enforced to match a common target posterior. They specify this constraint as:

\[\argmin_{q \in Q} \mathbb{E}_c [ \mathcal{D}_{KL}( q(\mathbf{z}|\mathbf{x}_c,\phi_c) \| p(\mathbf{z}|\mathbf{x}_1,\dots,\mathbf{x}_C,\theta) ) ]\]

where \(Q\) represents a family of distributions parametrized by \(\{\phi_i,\dots,\phi_C\}\).

The authors use Bayes theorem on the intractable posterior \(p(\mathbf{z}|\mathbf{x})\) to arrive at a lower bound formulation that optimizes the same objective as their constraint. Finally, since all the channels are projected to a shared latent representation, they can be assumed independent from each other conditioned on the latent representation, which allows the factorization of the data likelihood term \(p(\mathbf{x}|\mathbf{z})\) so that the final lower bound formulation is:

\[\mathcal{L} = \mathbb{E}_c [L_c - \mathcal{D}_{KL}( q(\mathbf{z}|\mathbf{x}_c) \| p(\mathbf{z}) )] \\ \text{where} \quad L_c = \mathbb{E}_{q(\mathbf{z}|\mathbf{x}_c)} \left[ \sum_{i=1}^C \ln p (\mathbf{x}_i|\mathbf{z}) \right]\]

Variational Dropout for Sparse Representation

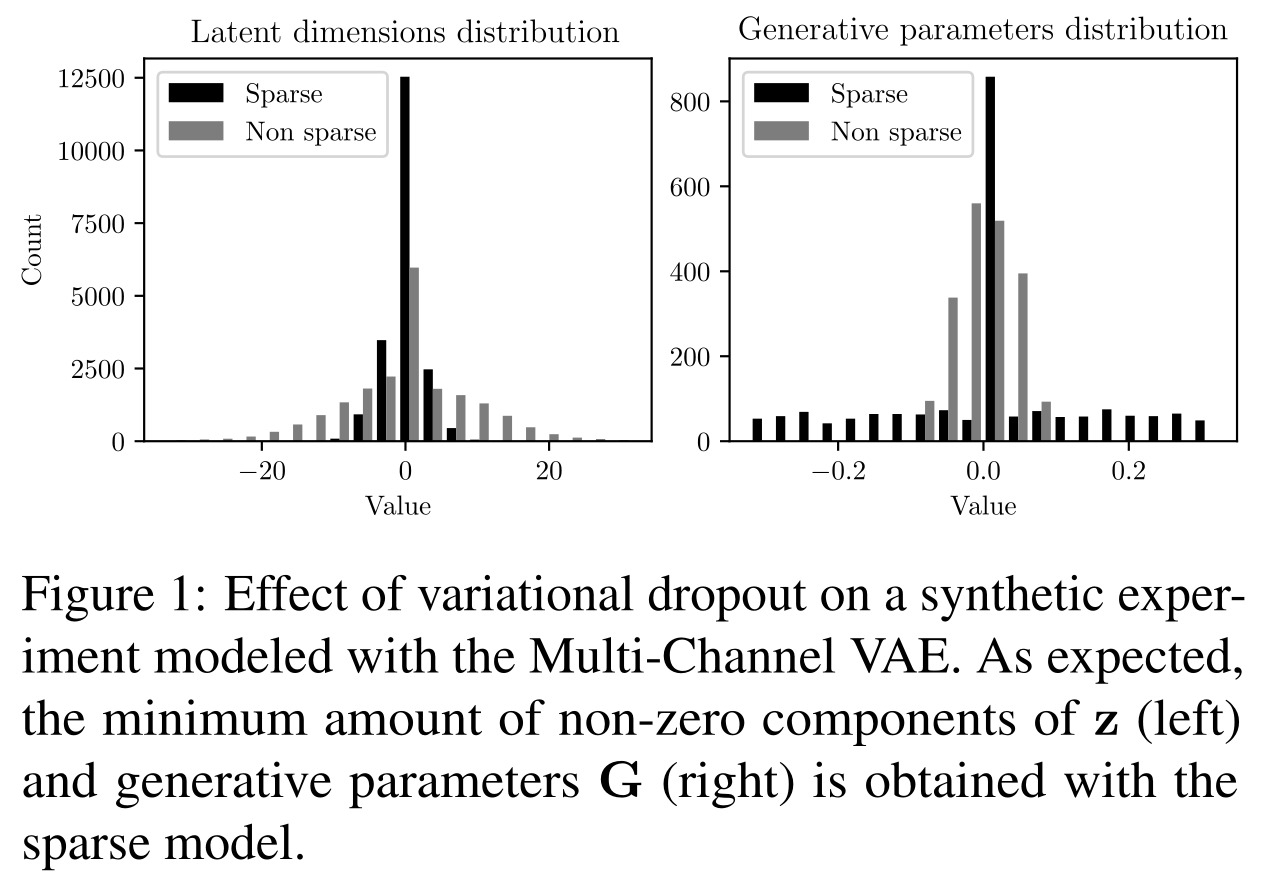
The authors state that in experiments with non-sparse, i.e. standard, models, the lower-bound was maximum at convergence when the number of latent dimensions matched the number of true generative factors.

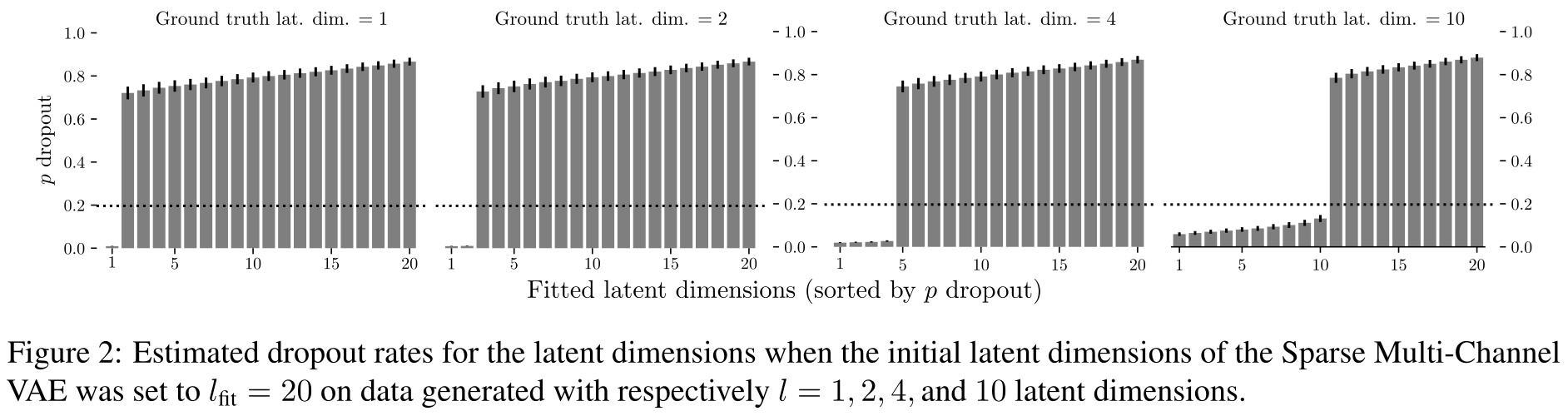
Thus, they propose to use sparsity constraints, through a form of dropout, to impose a parsimonious latent representation that learns in an unsupervised way to only use some of the latent dimensions available. After training, the “effective” latent dimensions can easily be identified by using a threshold on the dropout rates of each latent dimension.

Data

The authors first tested their method on synthetic data where they produce multiple channels with some correlations between them. They gain some insight into how their model works, e.g. a threshold on the dropout rates that discriminates useful latent dimensions from dimensions that can be pruned.

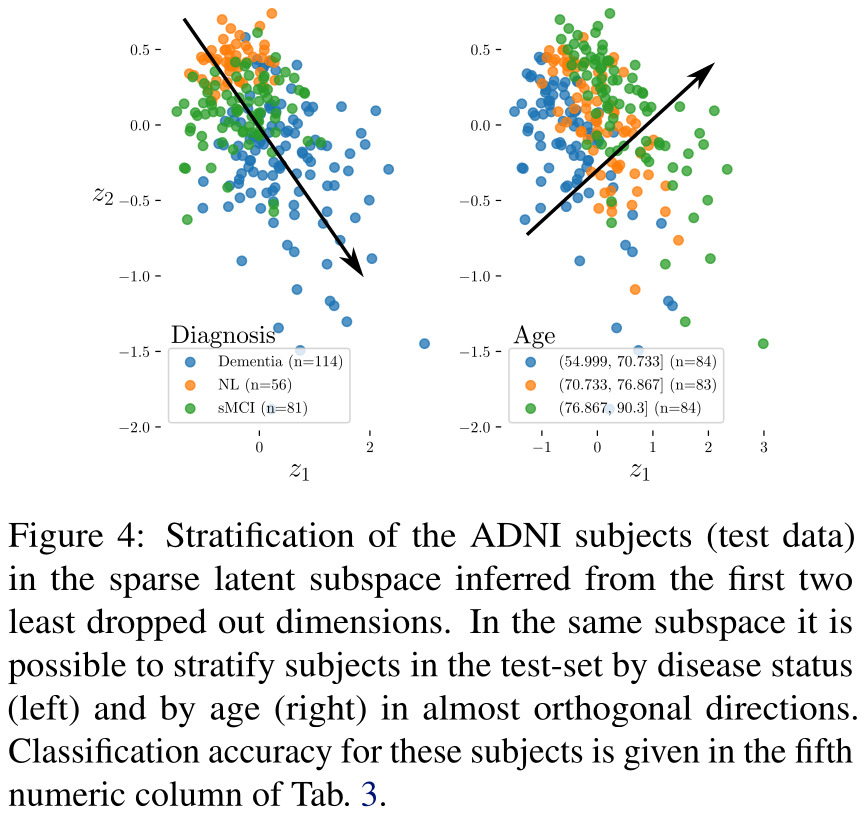
In a second experiment, the authors analyzed 504 subjects from the ADNI cohort1, studying Alzheimer’s disease using neuroimaging. The multi-channel data they used for each patient consisted of 3 imaging modalities (structural MRI of the gray matter only, functional FDG-PET and Amyloid-PET) and 6 clinical channels (age, results to mini-mental state examination, adas-cog, cdr, faq tests, and scholarity level) represented by continuous variables.

Results

References

  1. ADNI database website: http://adni.loni.usc.edu ↩