Introduction

Given a patient and dMRI acquisitions taken at two hospitals on the same day, we would expect these two images to be almost identical. However, the model of the scanner and the scanning protocol influence the images. The goal of dMRI harmonization is to remove site information from the images, such that it is not possible to tell from which site it comes, while still keeping the rest of the information. In this approach, a VAE is trained such that the decoding is conditioned on a site; this allows to convert images from one site to another. This method allows to harmonize data by choosing a reference site and converting all images to it.

The authors claim that their method does not require a paired dataset for training, while LinearRISH (Mirazaalian et al. ¹) requires it. (A paired dataset contains images from multiple sites for each subject; e.g. if there are 2 sites, each subject has a pair of acquisitions, one per site.) However, it has been shown that LinearRISH can be used with unpaired data². The advantage of this new method seems to lie in its lower error metrics.

Method

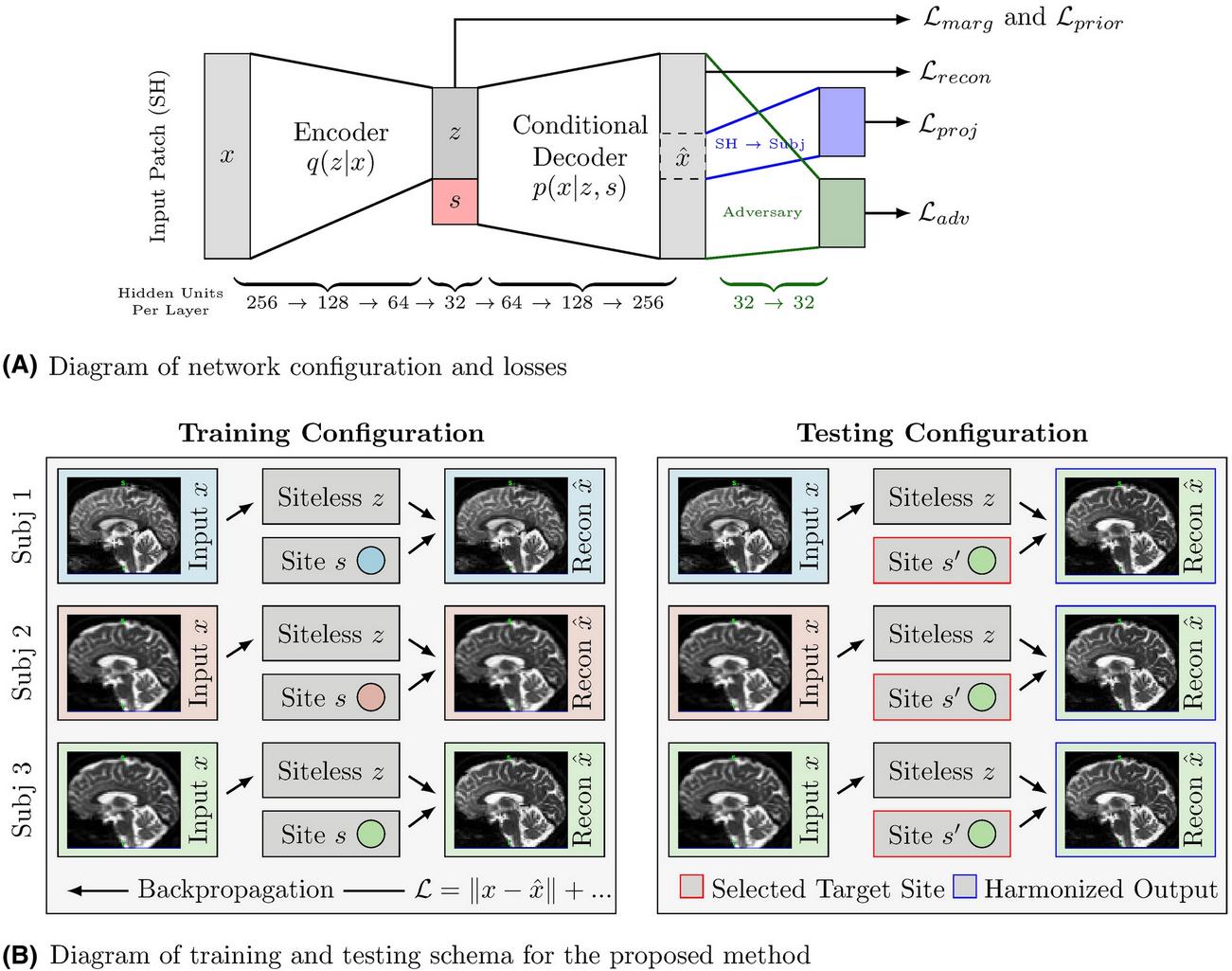
Trainable modules

• Encoder that maps \(x\) to \(z\)
  • \(x\) is a patch of SH (center voxel + 6 neighbors)
  • \(z\) has minimal site (\(s\)) information
• Decoder that maps \((z, s)\) to \(\hat{x}\)
  • \(\hat{x}\) is constructed such as it seems to come from site \(s\).
• Adversarial predictor to predict true/fake from \(\hat{x}\). The real images come from the dataset.
• Dense layer (transformation matrix) to project SH back to DWI

Losses

• Reconstruction loss (MSE) on \(\hat{x}\)
• Gaussian prior loss on \(z\)
• Marginal prior loss on \(z\) (minimizes the mutual information of \(z\) and \(s\))
• Adversarial loss (the typical approach from GAN training)
• Loss for the SH-to-DWI projection (no mention of which kind in the paper!)

Data

The CDMRI Challenge Harmonization dataset was used.

• 15 subjects (10 for training-validation, 5 for testing)
• 2 scanners (Prisma, Connectom)
• 2 protocols (One with 30 diffusion directions, one with 60; there are other differences, but the number of directions in the main difference)
• 2 x 2 = 4 sites (Prisma 30, Prisma 60, Connectom 30, Connectom 60)
• 10 x 4 = 40 acquisitions in the training set

See paper for preprocessing details.

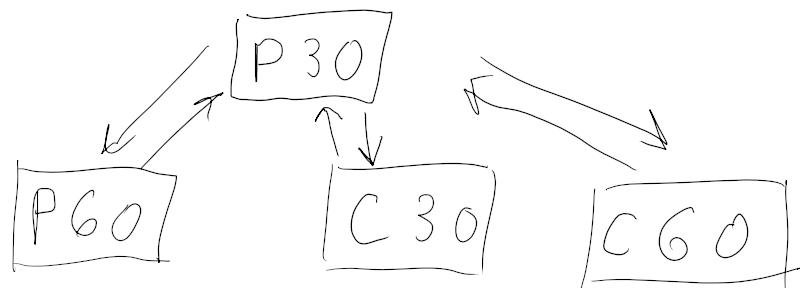
Tasks

• Map Prisma 30 to Connectom 30 and back
• Map Prisma 30 to Prisma 60 and back
• Map Prisma 30 to Connectom 60 and back

Evaluation

They perform extensive evaluation:

• Metrics: computed on FA (fractional anisotropy), MD (mean diffusivity), MK (mean kurtosis) and RTOP (return to origin probability): APE (absolute percent error) and CV (coefficient of variation)
• Ablation tests
• Post-hoc adversary: train a site predictor on the latent vector \(z\); and make sure we can’t predict the site from it
• Baselines:
  • LinearRISH (Mirzaalian et al. ¹)
  • Single-site variant of their own method, where one VAE is trained for each site transition (??? confirm this)

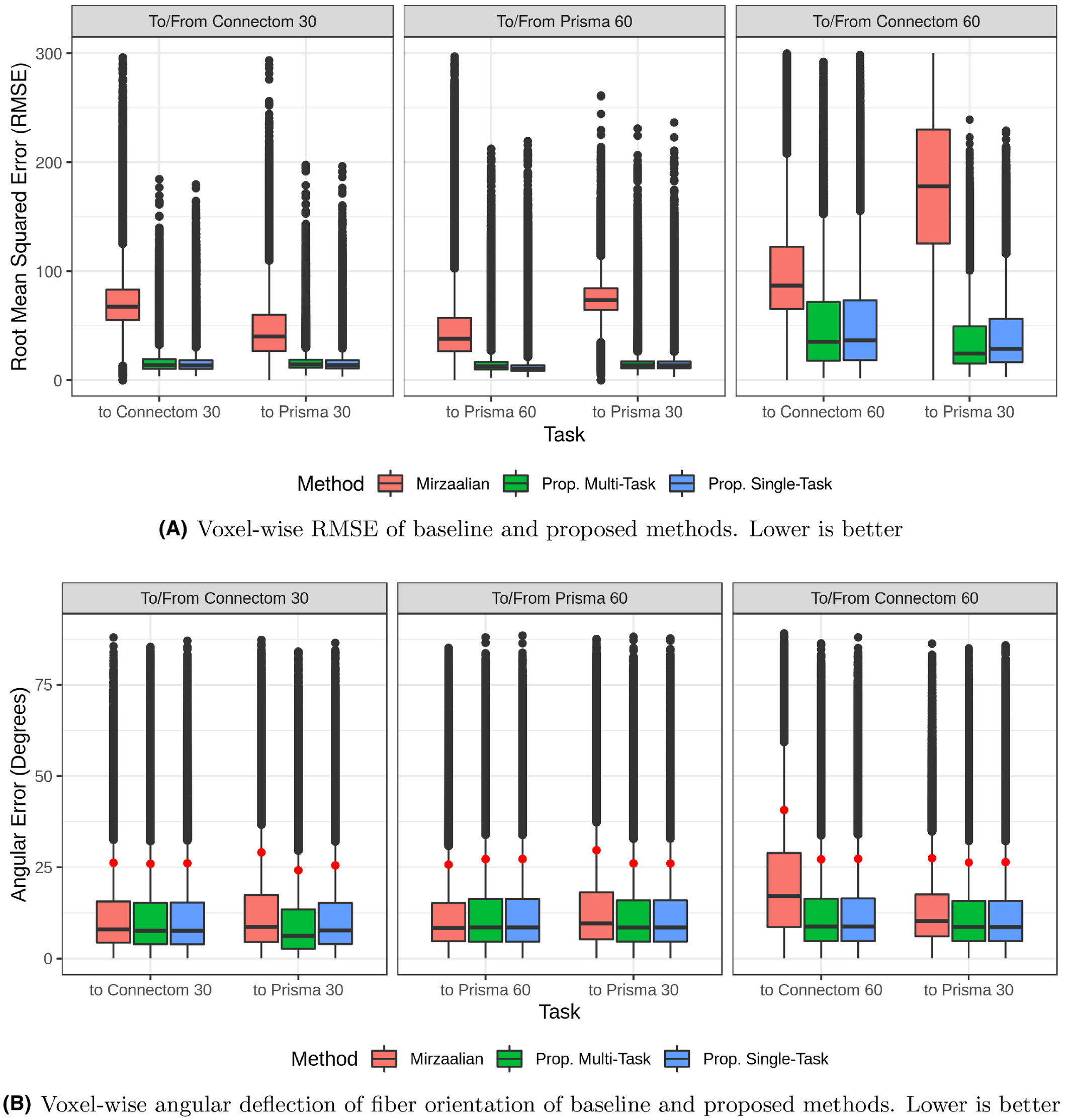
Reconstruction results

The following plot shows the error between the reconstructed signal and the true signal:

Site prediction from \(z\)

The post-hoc adversary is able to tell the correct site using the latent vector \(z\) 41% of the time (random chance is 25%). It’s hard to tell how good this value is. It’s clear that \(z\) does contain some site information. Still, the reconstruction results suggest that the method is better at harmonizing than the baseline.

Conclusion

This methods significantly beats the LinearRISH baseline as evaluated here (RMSE on the true images, small and balanced dataset). The amount to which this new method can generalize and can be trusted remains to be discovered. For instance, it may not tolerate site imbalance as well as LinearRISH.

References and notes