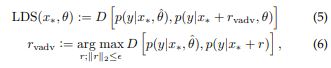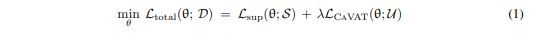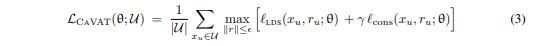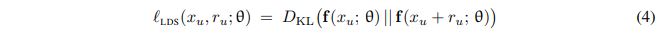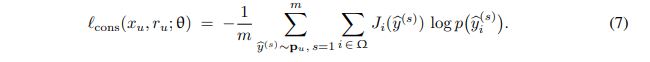Introduction

Authors tackle the task of generating anatomically plausible segmentations using an adversarial training scheme while optimizing a non-differentiable loss function with the REINFORCE algorithm.

Authors start by listing a number of methods that attempt to add constraints to neural network training such as size constraints and centroid positions. These constraints require differentiable loss functions which limit their use. Authors would like to exploit the information contained in anatomical shape priors like in Oktay et al., 2017 (ACNN), Zotti et al., 2018 (Prior-aware segmentation) and Painchaud et al. 2020.

Authors explore the aspect of semi-supervised learning as training segmentation networks to learn valid shapes is a difficult task when little labeled data is available. Authors, therefore, propose a method base on Virtual Adversarial Training (VAT) and REINFORCE to optimize a non-differentiable local connectivity constraint.

Method

Note on VAT

The goal of the VAT paper ¹ (Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning) is to propose a method for semi-supervised learning based on regularization induced by adversarial perturbations. The loss is given by:

Here, an adversarial perturbation is generated using gradient descent to maximize the divergence in predictions of the network.

Training

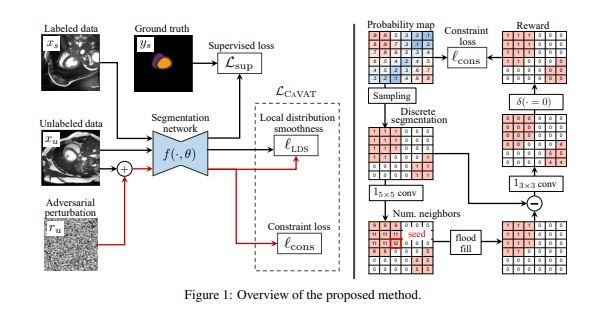
Training the proposed method is done on a labeled set \(\matcal{S}\) and an un-labled set \(mathcal{U}\). The network is trained using the following loss function.

The supervised loss \(\mathcal{L}_{sup}\). The Context-aware VAT loss term is composed of two losses.

The first loss is the local distribution smoothness (LSD), which is directly taken from VAT. This loss regularizes the network by making it more robust to examples that violate the virtual adversarial direction.

The reinforced constraint loss is given by

where \(J\) is the per-pixel reward and \(p_u = f(x_u+r_r;\theta)\) is the probability output of the network.

Looking back at equation (3), we can note here that the adversarial perturbation \(r_U\) is maximized on both terms of the CAVAT loss which increases the number of samples that violate the constraint.

Local connectivity constraint

The constraint optimized in this paper is the local connectivity constraint. Connectivity of a region G means that there exists a path between every pair of pixels in G such that every pixel in that path is also in G. As global connectivity is hard to achieve at the beginning of training, authors propose to optimize local connectivity at local patches.

Given a discrete prediction \(\hat{y}\), the authors apply a \(1_{ l\times l}\) convolution to find the pixel with the most neighbors (\(l=5\)). They then apply a flood-filling algotithm starting at this pixel to identify its region C. For each \(k \times k$ patch, the authors find the pixels (S) not in C using a convolution\)S=1_{k \times k} \circledast (\hat{y} - C)\((\)k=3\(). Finally the reward for each pixel\)i\(is given by\)J_i(\hat{y}) = \delta(S_i) = 0) \(where\)\delta(\cdot)$$ is the Kronecker delta.

Results

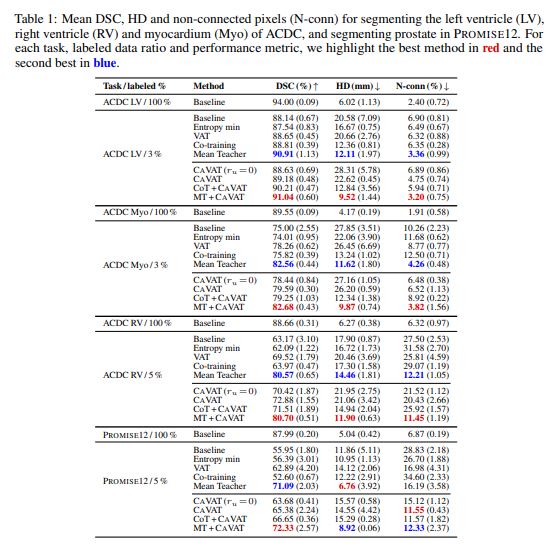
Authors test their method on binary segmentations of the structures in the ACDC heart segmentation dataset (LV, RV, MYO) and on the Prostate MR Image Segmentation (PROMISE12) Challenge dataset.

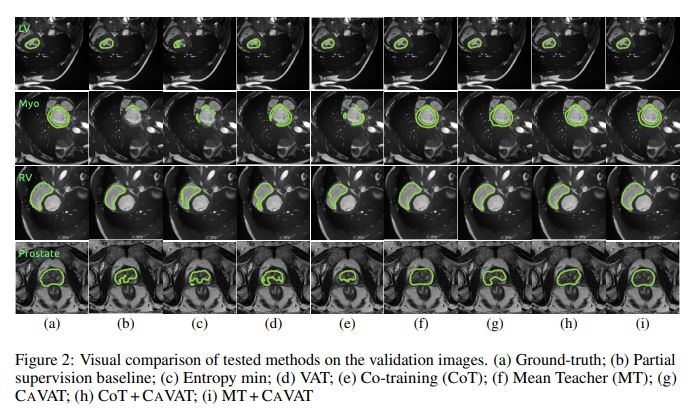
They compare their method with other state of the art semi-supervised learning and evaluate on Dice score (DSC), Hausdorff distance (HD) and percentage of non-connected pixels (N-conn). As the methods works on top of any semi-supervised segmentation method, the authors also propose combining their method with other methods such as Mean Teacher² (MT + CAVAT) and Co-training³ (CoT + CAVAT).

Conclusion

The authors propose an interesting method to correct anatomical errors during training. Their method however requires to be combined with other methods to be successful and produces only marginally better results than these methods alone.

References