Highlights

  • New deterministic Regularized Autoencoder (RAE) that can serve as a drop-in replacement for VAEs;
  • Ex-post density estimation scheme to improve sample quality for VAEs by not assuming the aggregate posterior matches the prior.

Introduction

The authors propose that while theoretically sound, the VAE framework poses a few problems, e.g. stochasticity, MC estimates of reconstruction expectation, etc., that rely on tricks and assumptions to work in practice. They emphasize that the common implementations of VAEs boil down to augmenting the decoder’s input with Gaussian noise, and they propose to theoretically consider VAEs in that perspective.

They also refer to an exhaustive literature in recent years that suggests implicit regularization in neural networks, through methods like batch normalization, dropout, etc., already smooths the functions learned by convnets, and that autoencoders might not need to enforce an explicit prior on the latent space for it to be smooth.

Methods

Deterministic Regularized Autoencoders

Under the perspective that VAEs are deterministic autoencoders with added noise, the authors explain that this noise is in fact a key mechanism in regularizing the decoder. Thus, they propose to “substitute noise injection with an explicit regularization scheme for the decoder”.

The loss that a RAE minimizes can thus be formulated as:

\[\mathcal{L}_{RAE} = \mathcal{L}_{REC} + \beta \mathcal{L}^{RAE}_{Z} + \lambda \mathcal{L}_{REG}\]

where \(\mathcal{L}^{RAE}_{Z} = \frac{1}{2}\|z\|^2_2\) is there to constrain the size of the latent space and prevent unbounded optimization.

\(\mathcal{L}_{REG}\) is a regularization to enforce on the decoder, and the authors propose multiple variants:

  • L2: Tikhonov regularization, related to low-magnitude input noise, which amounts to applying weight decay to the decoder parameters: \(\mathcal{L}_{L_2} = \|\theta\|^2_2\);
  • Gradient penalty: Gradient penalty comes from recent GAN literature on regularization, where it is used on the discriminator, bounds the gradient norm: \(\mathcal{L}_{GP} = \|\nabla D_{\theta}(E_{\phi}(x))\|^2_2\);
  • Spectral normalization: Still taken from GAN literature, spectral normalization normalizes weight matrices by an estimate of their largest singular values: \(\theta^{SN}_{\ell} = \frac{\theta_{\ell}}{s(\theta_{\ell})}\).

They also consider a model without an explicit regularization on the decoder (referred to as RAE in the results), since they were curious to investigate if training techniques like dropout, batch normalization, etc., would implicitly regularize the network enough.

Ex-post Density Estimation

Removing the KL divergence term from RAEs, the authors acknowledge that they have detached the encoder from the prior \(p(z)\) that could help guide sampling from the learned distribution. However, they argue that the mismatch between the prior and aggregate posterior is a problem recognized even in VAEs.

Thus, they propose to fit a density estimator \(q_{\delta}(z)\) on the encodings of the dataset \(\{ z = E_{\phi}(x) \mid x \in \mathcal{X} \}\). This way, their ex-post density estimation requires no additional training, and can be used with any autoencoder.

In their experiments, the authors use either a Gaussian or a mixture of 10 Gaussians as \(q_{\delta}(z)\).

Data

The authors report image modeling results on MNIST, CIFAR10 and CelebA. The paper also reports results for structured inputs, using what they call a GrammarRAE, on mathematical expressions and molecules.

Results

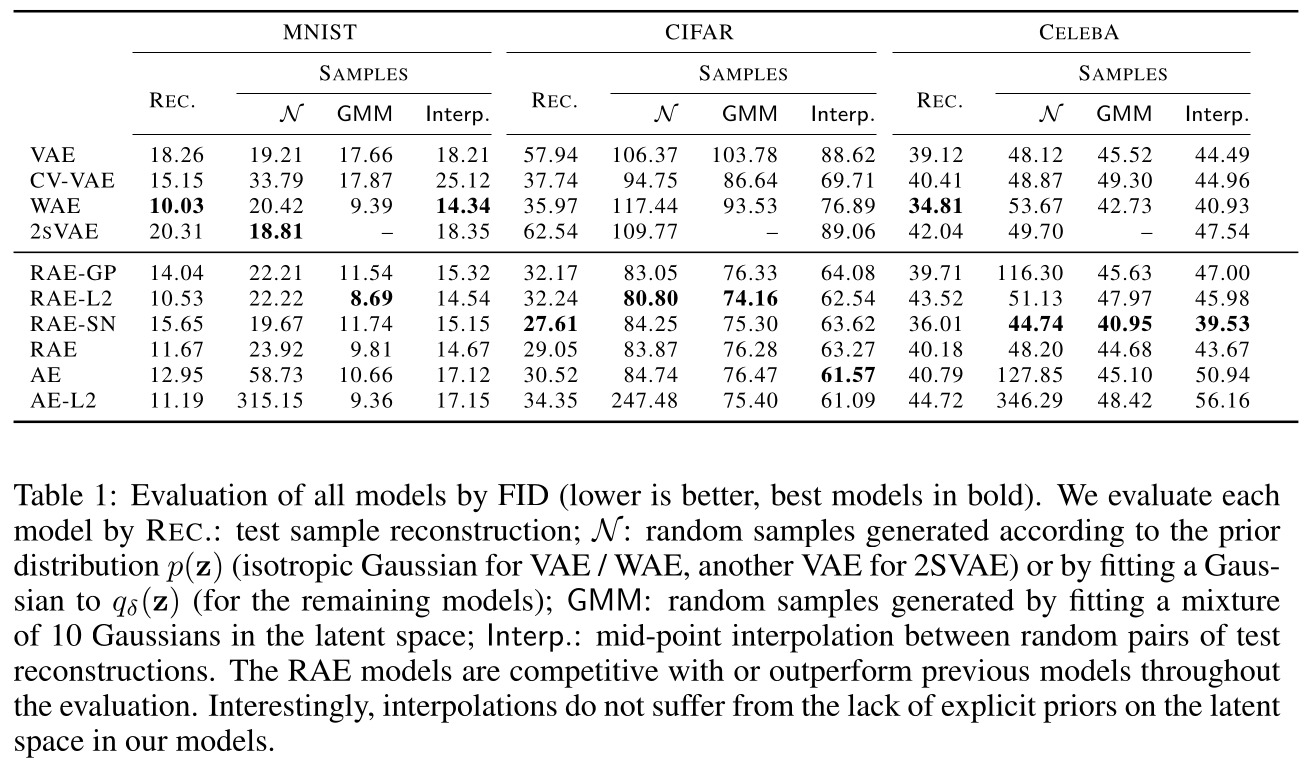
Supplementary results

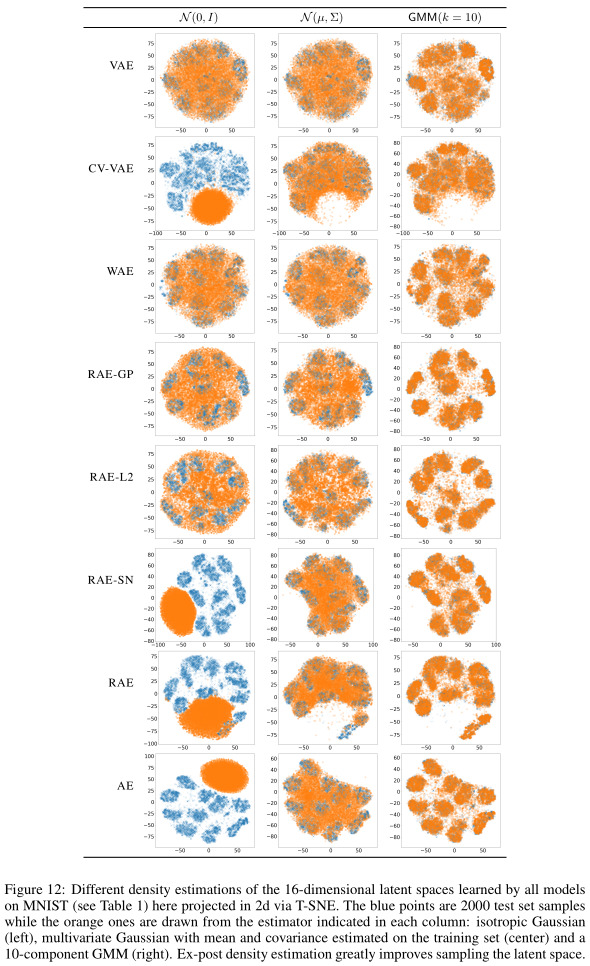
Remarks

  • The ex-post density estimation is underwhelming given the depth of the analysis in the rest of the paper. Intuitively, it doesn’t seem that a mixture of gaussians would scale well to model arbitrary aggregate posterior distributions. Their 10-component GMM might also work particularly well because it was mostly tested on datasets with 10 classes, i.e. MNIST and CIFAR.

References