Highlights

• Authors propose a self-supervised, deep convolutional neural network-based strategy to perform the fiber clustering task in an anatomically informed manner.
• Undesired fibers are rejected using soft label assignment probabilities.
• Multi-subject fiber cluster atlases can be created to be applied to new subjects.

Introduction

Tractography generates hundreds of thousands of fibers that are not immediately useful to clinicians. Among others, fibers need to be clustered into anatomically meaningful groups for such purpose. Conventional methods face a number of challenges, including (i) long computation times; (ii) fiber point ordering asymmetry; (iii) presence of outliers; (iV) a trade-off between anatomical coherence and local fiber coordinate information; and (v) inter-subject correspondence of fibers.

They propose to deal with these challenges using a self-supervised, anatomically informed deep convolutional neural network-based model.

Methods

Their method includes two stages:

• A pre-training stage: a self-supervised learning strategy is adopted with the pretext task of pairwise fiber distance prediction using embedded fiber representations. A \(k\)-means clustering is performed to get initial clusters.
• A clustering stage: a clustering layer is connected to the embedding layer and generates soft label assignments, refining the clustering results of the previous stage. A KL divergence loss and the prediction loss are combined to optimize the neural network.

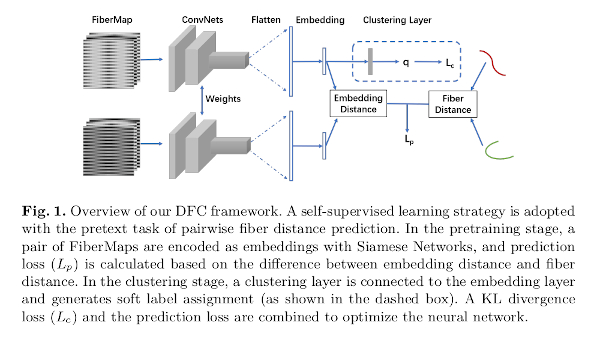
The fiber distances used in the pretext task are the MDF, which is not affected by fibers whose point sequence is flipped¹.

The fibers are represented as feature vectors (called FiberMaps) that combine streamline vertices in both orientations following an earlier work from the same authors². Fibers are dowsampled to 14 points to obtain the FiberMaps.

During inference, cluster assignments are obtained end-to-end on a new subject without any \(k\)-means step.

The clustering stage is based on a modified version of the DCEC³ model in order to incorporate the anatomical information. An additional term is added to the soft assignment label (i.e. probability) that accounts for the Dice score between the set of regions of a given fiber (according to an atlas) and the set of regions of a given cluster. Additionally, fibers that have a soft label value lower than a given threshold are removed (outlier rejection).

The total loss is the weighted sum of the terms of the two stages:

\[L = L_{p} + \lambda L_{c}\]

where \(L_{p}\) is the distance prediction loss, \(L_{c} = KL(P \mid\mid Q) = \sum_{i} \sum{j} p_{ij} \log \frac{p_{ij}}{q_{ij}}\), and \(\lambda\) is a weighting term.

In the above equation,

\[p_{ij} = (q_{ij}^{2} / \sum_{i} q_{ij}) / (\sum_{j'} q_{ij'}^{2} / \sum_{i} q_{ij}))\]

where \(q_{ij}\) the soft assignment label (that follows a Student’s t-distribution), i.e. the probability of assigning fiber \(i\) to cluster \(j\), and is computed as:

\[q_{ij} = (1 + \lVert z_{i} - \mu_{j} \rVert^{2} * (1 - D_{ij}))^{-1} / (\sum_{j'} (1 + \lVert z_{i} - \mu'_{j} \rVert^{2} * (1 - D_{ij} 0 ))^{-1})\]

where \(z_{i}\) is the embedding of fiber \(i\); \(\mu_{j}\) is the centroid of cluster \(j\); and \(D_{ij}\) is the Dice score between the set of (Freesurfer) regions of fiber \(i\) and the set of Freesurfer regions of cluster \(j\).

During inference, a fiber \(i\) is assigned to the cluster with the maximum \(q_{ij}\).

Data

200 subjects of the HCP are used (split as 100/50/50 for training/validation/testing).

For each training subject, 10000 random streamlines were selected, giving a total size of 1M training streamlines. For validation and testing, whole-brain tractography fibers (around 500k) were used.

Streamlines below 40 mm were discarded from the tractograms.

Evaluation

Quality measures:

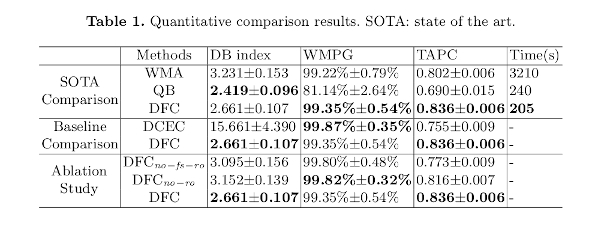
• Davies-Bouldin (DB) index:

\[DB = (1/n) \sum_{k=1}^{n} max_{x \neq y} \frac{\alpha_{i} + \alpha_{j}}{d(c_{i}, c_{j})}\]

where \(n\) is the number of clusters, \(\alpha_{i}\) and \(\alpha_{j}\) are mean pairwise intra-cluster fiber distances, and $d(c_{i}, c_{j})$ is the inter-cluster fiber distance between centroids \(c_{i}\) and \(c_{j}\) of cluster \(i\) and \(j\). A smaller DB score indicates a better separation between clusters.

• White Matter Parcellation Generalization (WMPG): represents the percentage of clusters successfully detected across the testing subjects.

• Tract Anatomical Profile Coherence (TAPC): measures if the fibers within a cluster \(c\) commonly pass through the same brain anatomical regions:

\[TAPC(c) = (\sum_{f = 1}^{NF(c)} Dice(TAP(f), TAP_{atlas}(c)))/NF(c)\]

Higher TAPC scores indicate better anatomical coherence.

Baselines are QuickBundles¹ and WMA².

Results

Quality measures:

Fiber clusters:

Outlier removal:

Conclusions

Authors presented a novel unsupervised deep learning framework for dMRI tractography clustering.

The proposed method shows improved performance over the compared baselines.

References