Highlights

Contributions:

• A careful choice of the decoder distribution in VAEs to improve the performance of naïve calibrated decoders, removing the need to tune the distortion vs. rate (i.e. the information between the prior and the posterior) trade-off parameter in \(\beta\)-VAEs.
• Novel technique, dubbed as \(\sigma\)-VAE, for optimizing the decoder variance analytically, without requiring the decoder network to produce it as an additional output.
• Their results improve sample quality on various datasets compared to different VAE and sequence VAE models.

Introduction

VAEs require careful manual tuning of the balance between two terms that correspond to distortion (data reconstruction) and rate from information theory (KL divergence): a model with low rate would not contain enough information to reconstruct the data, while allowing the model to have high rate might lead to unrealistic samples from the prior as the KL-divergence constraint becomes weaker.

\(\beta\)-VAEs allow to weigh the trade-off through the \(\beta\) weighting term. However, the parameter needs to be tuned for every dataset and model variant as a hyperparameter.

The paper revisits the idea of learning calibrated decoders. Most VAE models are employed with uncalibrated decoding distributions, such as Gaussian distributions without a learned variance, where the decoder only outputs the mean parameter.

The work proposes a method to calibrate uncertainties for the likelihood in VAEs, i.e. a VAE model in which the variance is learned rather than chosen as a fixed hyperparameter.

Calibrated decoders

Due to various reasons (numerical instability, poor results of naïve approaches), calibrated decoders have not gained larger adoption by practitioners.

Gaussian decoders with the common MSE reconstruction loss assume a particular, constant variance of the Gaussian distribution, which is a limitation.

The calibration of a neural network can be usually improved by estimating the uncertainty of that prediction, such as the variance of a Gaussian. Since the naïve MSE loss assumes a constant variance, it does not effectively represent the uncertainty of the prediction. Thus common VAEs using the MSE reconstruction loss are poorly calibrated.

Authors propose to learn the variance (i.e. calibrate the decoder) to achieve a better performance.

Methods

Learning the variance can be done by letting a neural network \(\sigma_{\theta}\) output the diagonal entries of the covariance matrix given a latent sample \(z\):

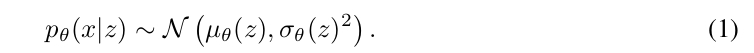
A simpler and more stable parameterization is to specify the covariance matrix as a diagonal matrix with single shared parameter across pixels \(\Sigma = \sigma^{2} I\):

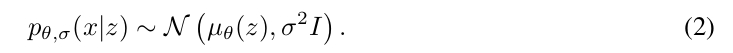
The parameter \(\sigma\) can be optimized together with parameters of the neural network \(\theta\) with gradient descent.

The objective function is:

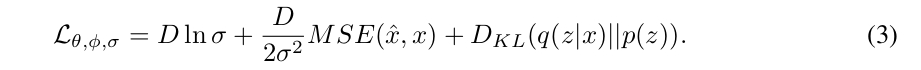
Authors propose alternatively an analytic expression, named optimal \(\sigma\)-VAE to obtain a calibrated decoder where \(\sigma\) can be computed from the training data as:

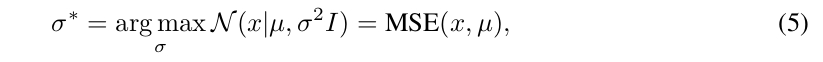
Finally authors propose to learn \(\sigma\) on a per-image basis.

Optimal \(\sigma\)-VAE uses a single variance value shared across all data points. However, their \(\sigma\)-VAE formulation also allows to learn a variance value per each image, the difference in implementation simply being the dimensions across which the averaging occurs.

Their strategy allows the weight on the KL divergence term to be set to one, as the new expression automatically balances the two terms of the objective. It is in fact a generalization of a \(\beta\)-VAE where the variance is not a constant term.

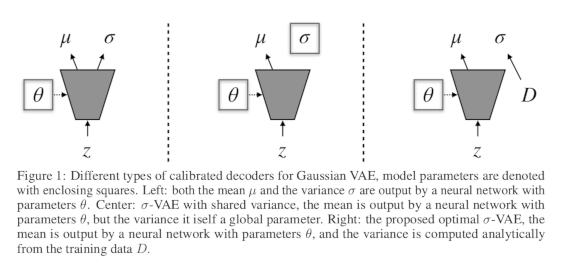
Data

Authors applied their method both for still pictures and videos:

• Still pictures
  • CelebA
  • CIFAR
  • Frey Face
  • MNIST
  • SVHN
• Videos
  • BAIR action free robot pushing dataset

Results

Results show that their method is superior in terms of log-likelihood/ELBO and FID against the baselines in the tested datasets.

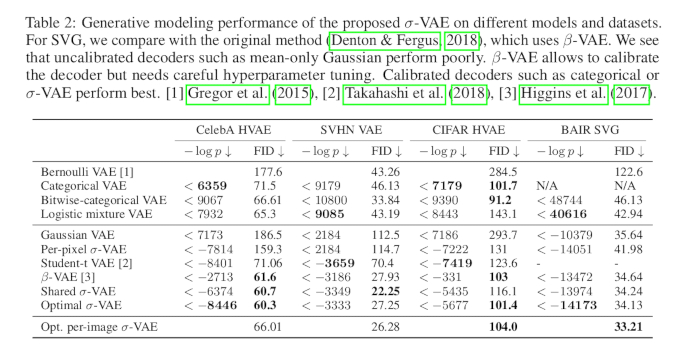
Note: FID is the Fréchet Inception Distance, which is used to evaluate the quality of images generated in generative contexts.

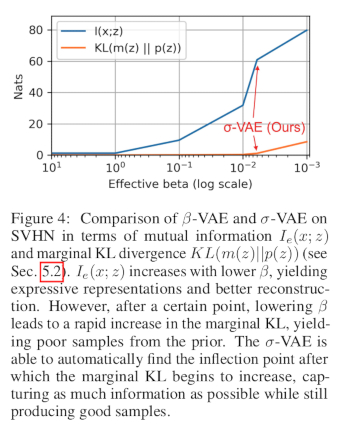
To investigate whether calibrated decoders are also beneficial for representation learning, authors evaluate the latent variable information content analyzing the mutual information \(I(x;z)\) between the data and the encoder samples \(q(z \mid x)\), as well as the mismatch between the prior \(p(z)\) and the marginal encoder distribution \(m(z) = E_{p_{d(x)}} = q(z \mid x)\), measured by the marginal KL \(D_{KL} (m(z) \mid\mid p(z))\):

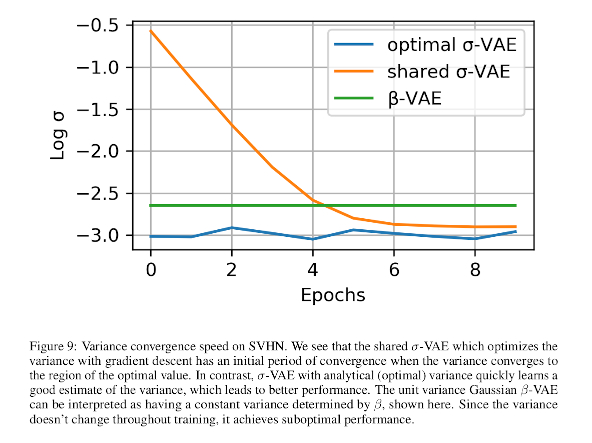
Optimal variance convergence:

Conclusions

Authors propose a method, dubbed as \(\sigma\)-VAE, to learn the variance of the decoder so that the decoding distribution is calibrated.

Their strategy allows the weight on the KL divergence term to be set to one (i.e. to avoid the empirical search of the \(\beta\) parameter of the \(\beta\)-VAEs).

Comments

Although the sampled faces by their \(\sigma\)-VAE do have finer details compared to the regular VAE, some image do contain results that introduce some visible artifacts. As reviewers point, might be due to not having trained the models long enough.

Authors have a website about the project/paper.