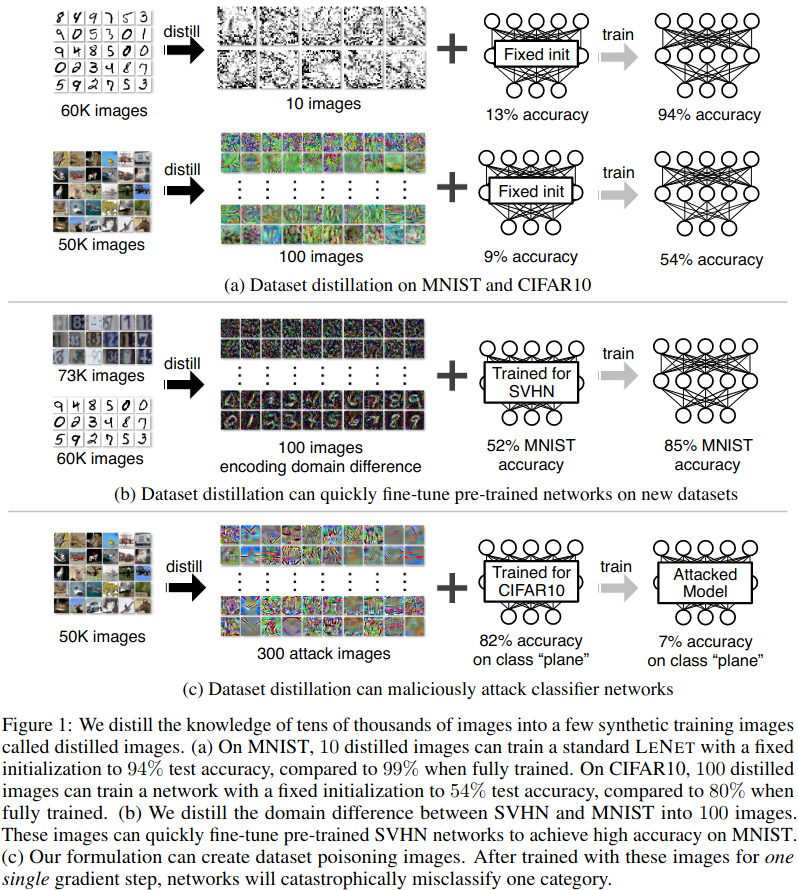
Highlights

The goal of this paper is to compress (yet distil) a dataset into a very small number of synthetic images that one can use to train the network in … 1 iteration!

Main idea

Given a minibatch \(\bm x_{t} = \{x_{t,j}\}_{j=1}^{n}\), a gradient descent step is simply:

\[\theta_{t+1} = \theta_{t} - \eta \nabla_{\theta_t}l(\bm x_{t},\theta_{t}).\]

The aim of this paper is to compute \(\tilde{\bm x}= \{\tilde{x}_{i}\}_{i=1}^{M}\) a set of M synthetic images (where M is much smaller than the size of the training set) as well as a learning rate \(\tilde{\eta}\) so a single gradient step can lead to some optimal solution:

\[\theta_1 = \theta_0 - \tilde{\eta}\nabla_{\theta_0} l(\tilde{\bm x}, \theta_0)\]

where \(\theta_0\) is the inital set of weights and \(\theta_1\) is the optimal set of weights. Given \(\theta_0\), \(\tilde{\bm x}\) and \(\tilde{\eta}\) are optimized as follows:

\[\tilde{\bm x}, \tilde{\eta} = \arg\min_{\tilde{\bm x}, \tilde{\eta}} l(\bm x,\theta_1) = \arg\min_{\tilde{\bm x}, \tilde{\eta}} l(\bm x, \theta_0 - \tilde{\eta}\nabla_{\theta_0}l(\tilde{\bm x},\theta_0)\]

and since that loss is differentiable wrt \(\tilde{\bm x}, \tilde{\eta}\), they can be computed with standard gradient descent. However, the authors argue that finding an optimal solution from one init set of weights \(\theta_0\) do not generalize well. As an alternative, they compute \(\tilde{\bm x}, \tilde{\eta}\) from serveral init weights \(\theta_0^j \sim p(\theta_0)\) as illustrated in Algorithm 1.

That is pretty much what the main idea of the paper is. The paper reports results from Random Init, Fixed Init, and pre-trained weights.

Results

Results are shown in the Fig.2 and 3. For MNIST they used LeNet CNN and for CIFAR10 AlexNet.