Highlights

The authors find two properties of neural networks.

There is no distinction between individual high-level units and random linear combinations of high-level units.
Existence and transferability of adversarial examples.

On the units

Let \(x \in \mathbb{R}^m\) be an input image and \(\phi(x)\) the activation values of some layer. One can look at what inputs maximize the features of \(\phi(x)\), that is:

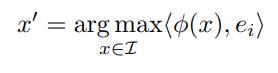
The authors find that many images that satisfy

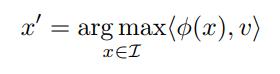
are semantically related to each other, where \(v\) is a random vector.

This puts into question the notion that neural networks disentangle variation factors across coordinates.

Adversarial examples

Let \(f:\mathbb{R}^m \to \{1,...,k \}\) be a classifier with an associated loss function. For a given input \(x \in \mathbb{R}^m\) and target label \(l \in \{1,...,k \}\), the aim is to solve

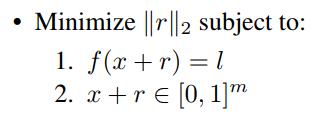
The minimizer is denoted \(D(x,l)\). This task is non-trivial only if \(f(x) \not= l\). The authors find an approximation of \(D(x,l)\) by line-search to find the minimum \(c>0\) for which the minimum \(r\) of the following problems atisfies \(f(x+r)=l\).

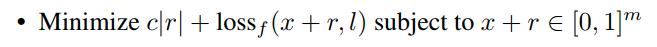
In the convex case this yields the exact solution.

Experiments

Existence of adversarial examples

Adversarial examples transfer to other architectures trained from scratch with different hyperparameters:

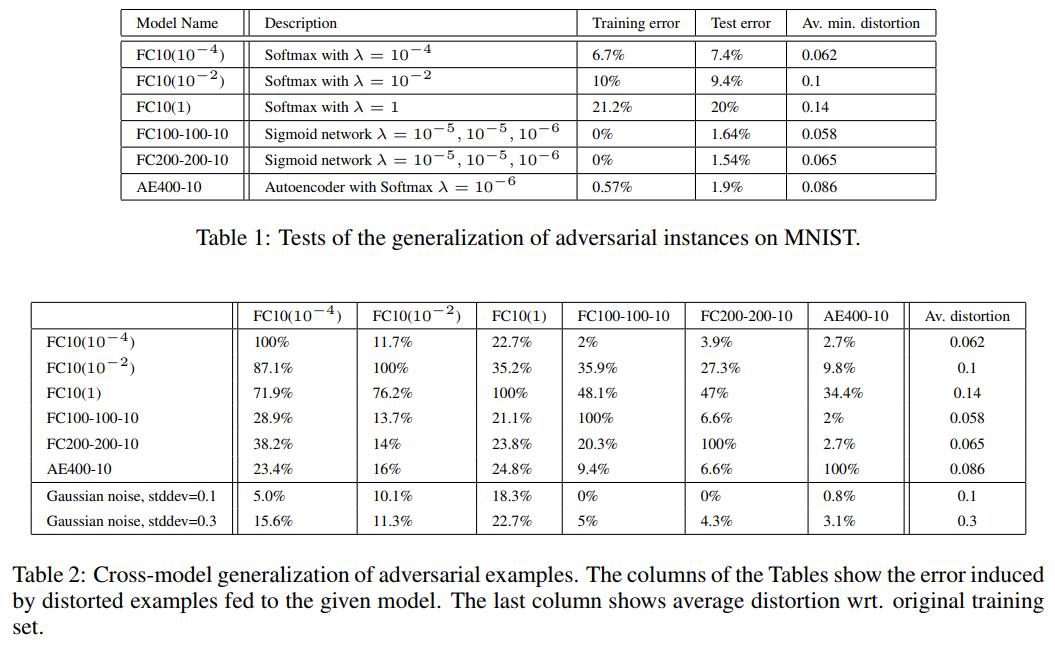
Adversarial examples transfer to other architectures trained on a disjoint training set:

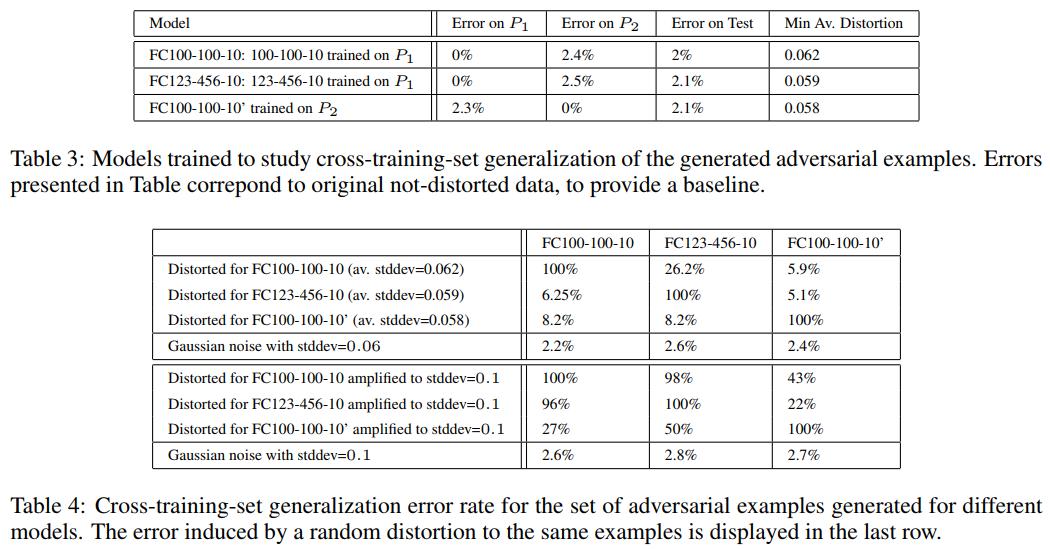
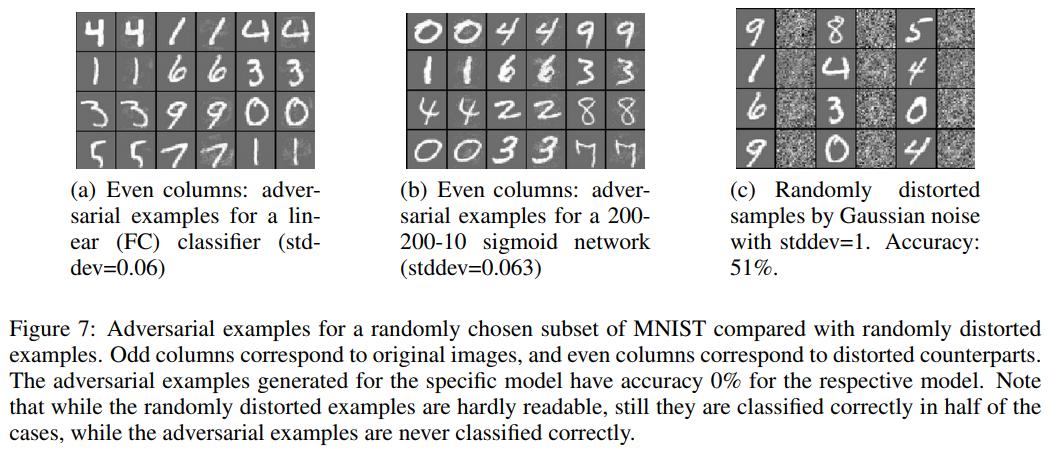
Adding random noise to the input images is not as effective to misclassify samples when compared to adversarial examples generation:

Theoretical analysis

Conclusion

The semantic meaning of activations of neurons is not meaningful since random directions in feature space present similar properties.
Adversarial examples can be found for any neural network, they transfer across architectures trained with different hyperparameters and even different data sets.