Highlights

• The authors propose an optimization method to generate adversarial examples for SVM and neural nets.
• The method has a regularization method that allows to generate adversarial examples in the black-box and white-box settings separately.
• They apply the method to malware detection in PDF files.

Introduction

Given a classification algorithm \(f: X \mapsto Y\) that assigns to a feature \(x \in X\) a label \(y \in Y = \{-1,+1 \}\), where \(-1\) represents the legitimate class and \(-1\) the adversarial or malicious class. The label \(y^c=f(x)\) given by a classifier is obtained by thresholding a discriminant function \(g : X \mapsto \mathbb{R}\), so we assume \(f(x)=-1\) if \(g(x) < 0\) and \(+1\) otherwise.

Adversary model

• Adversary’s goal: Find a sample \(x\) such that \(g(x)<-\epsilon\) for every \(\epsilon>0\). This means the sample just crosses the decision boundary. It can also be asked to find a sample where the classifier is highly confident on a wrong decision.

• Adversary’s knowledge: Depending on information about the classifier, data or training the adversary may find different strategies.

• Adversary’s capability: The authors restrict to scenarios where the adversary can only modify the test data.

Attack scenarios

• Perfect knowledge (PK): The adversary knows everything about the classifier: architecture, data, training.

• Limited knowledge (LK): The authors assume the adversary can generate a new dataset \(D'= \{ (\hat{x}, \hat{y}) \}\) on which to train a new classifier \(\hat{f}\) and discriminat function \(\hat{g}\) that approximates the original discriminant function \(g\) of the classifier \(f\).

Attack strategy

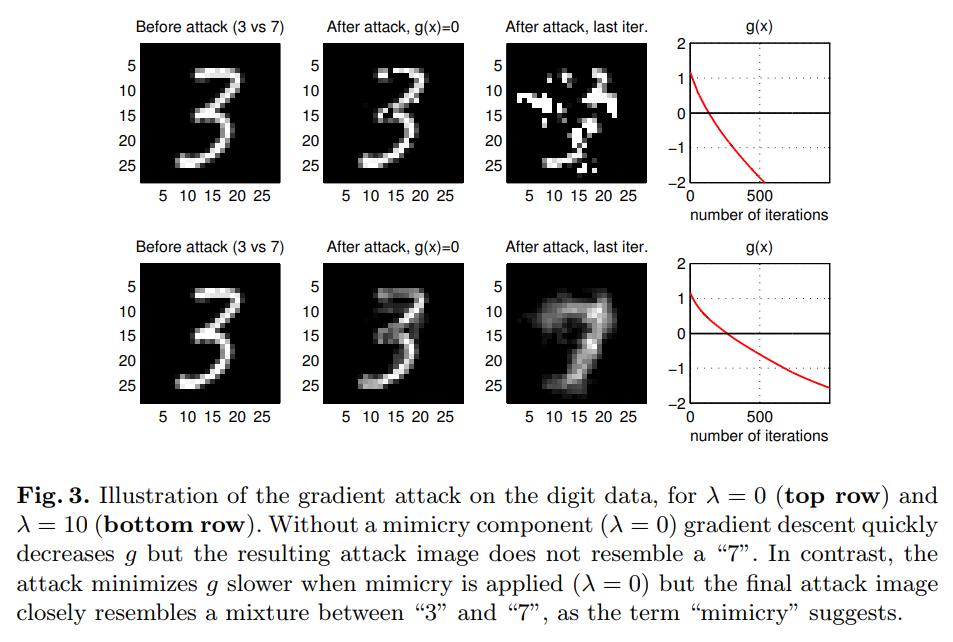
For an adversarial target sample \(x^0\), an optimal attack strategy finds sample a \(x^*\) to minimize \(g\) or its estimate \(\hat{g}\), subject to a bound on its distance from \(x^0\)

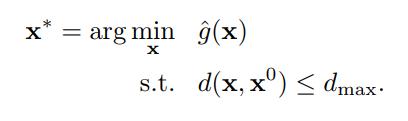
But this is hard, so they regularize it as follows:

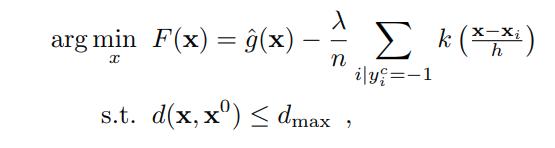
They approach this via gradient descent:

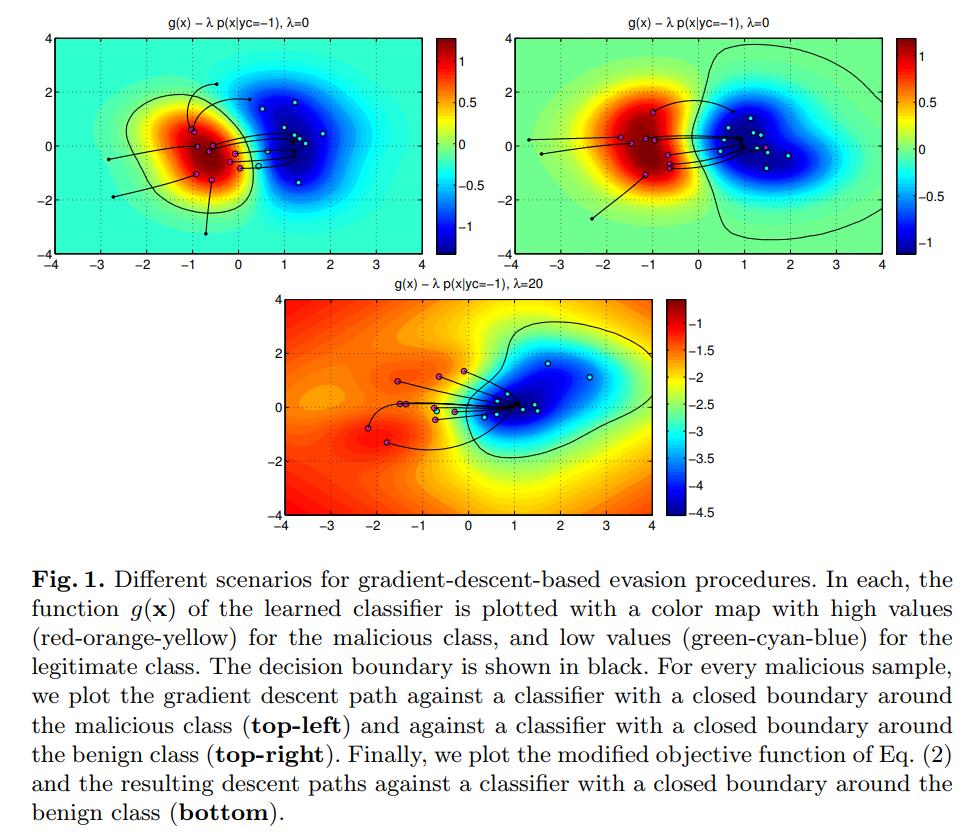
About the gradient

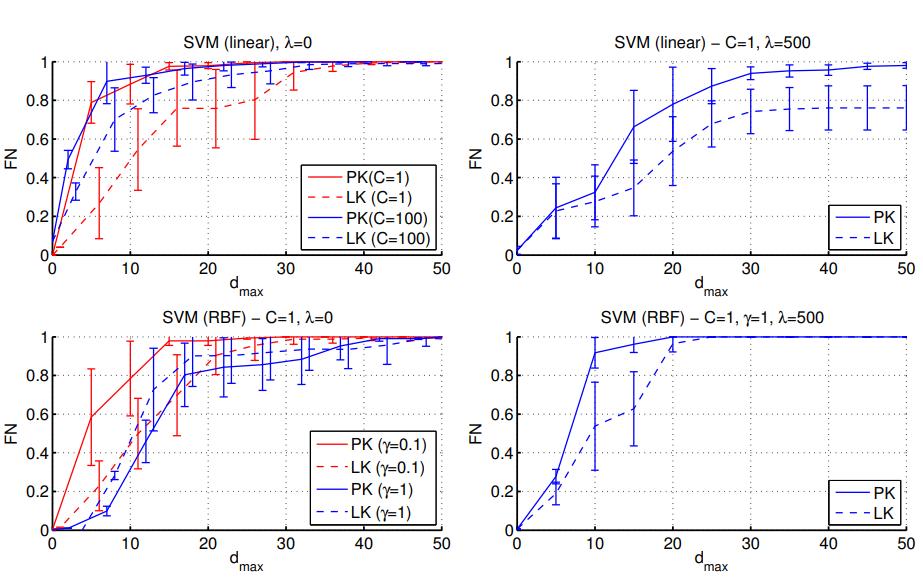
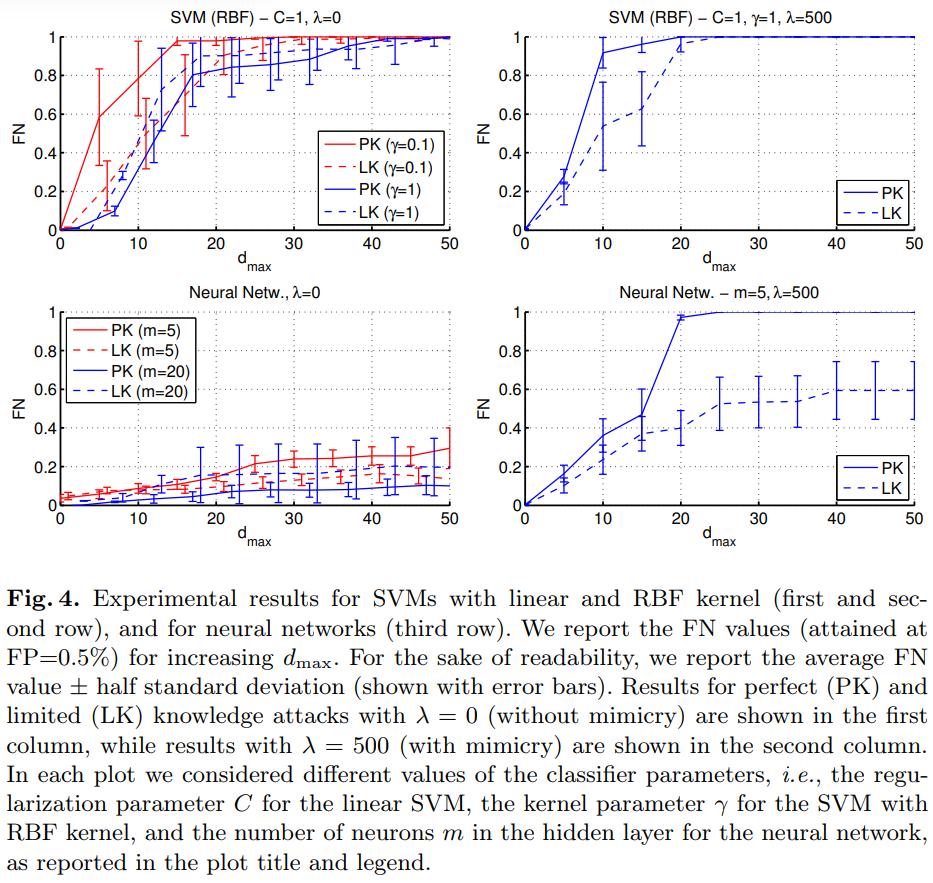
Experiments