Introduction

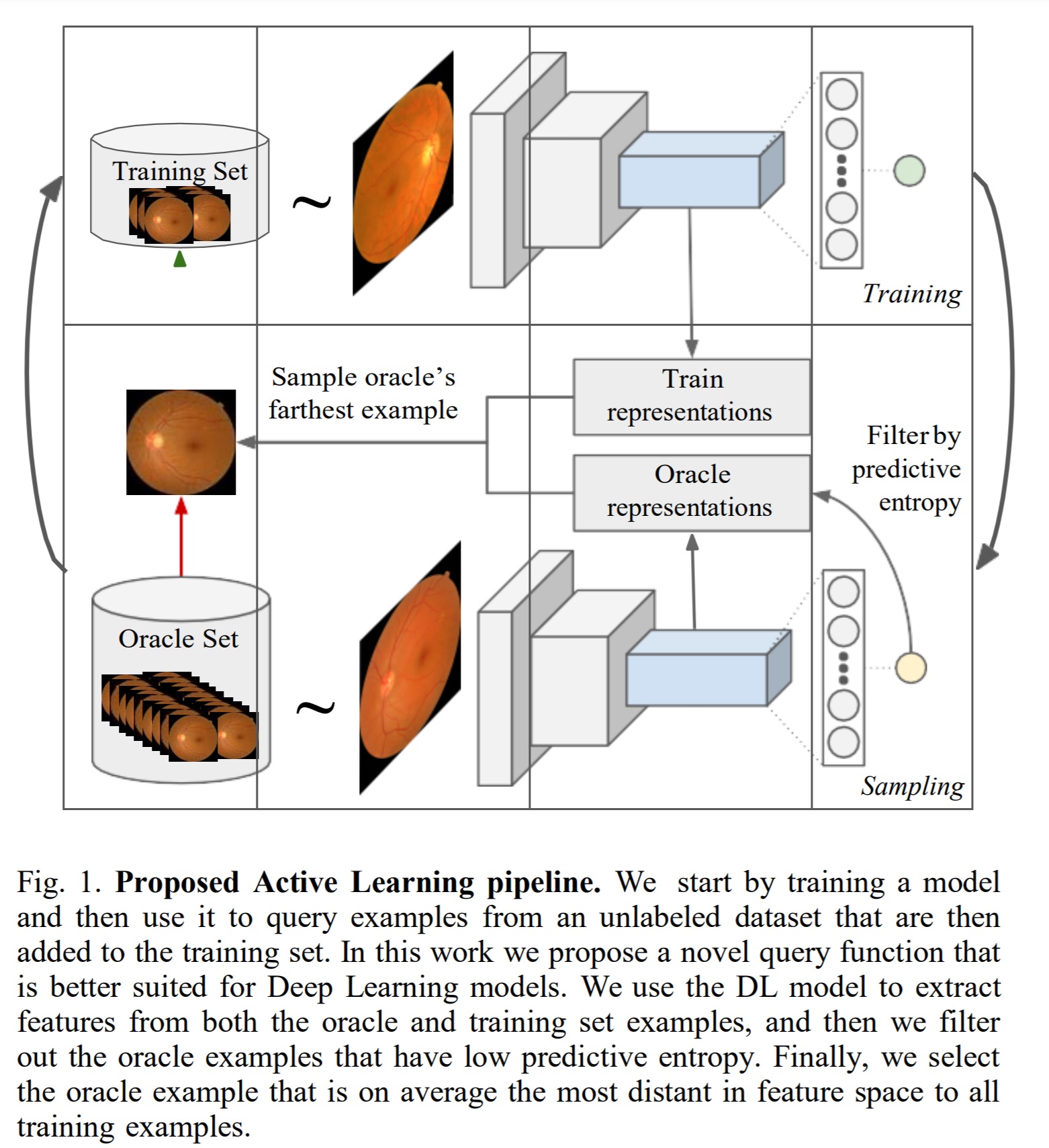
The authors introduce a novel method for active learning that aims to select more representative samples than standard active learning heuristics.

Summary of Contributions

Novel AL sampling method that maximizes the representativeness of samples selected for labeling.
Better initialization by selecting the initial pool with standard feature extraction and description methods

Existing Methods

Consider an empty training set \(D_{train}\) and an unlabeled dataset \(D_{oracle}\)

Standard Active learning loop

Label \(n\) samples from \(D_{oracle}\) and add them to \(D_{train}\) .
Train model on \(D_{train}\) .
Evaluate the model’s uncertainty on \(D_{oracle}\) .
Label \(n\) most uncertain samples and add them to \(D_{train}\) .
Repeat steps 2 to 4.

Many heuristics can be used to evaluate uncertainty.

Method

Sampling method

In this work, the authors use rich data descriptions \(f(x) \in R^n\) to select the most representative samples. This is done by evaluating the average distance with all the samples in \(D_{train}\).

\[\tag{1} s(x) = \frac{1}{N}\sum_{i=1}^N d(f(x_i), f(x))\]

where \(x_i \in D_{train}\).

The rich data descriptor \(f(x)\) used is a deep representation obtained from a layer in CNN trained for classification. The representations are therefore updated at every step.

To avoid computing this for each sample, \(s(x)\) is only computed on the \(M\) samples with the highest predictive entropy (authors do not mention this explicitly but computing \(s(x)\) for each sample in the oracle set would involve computing the distance function for every possible pair in the oracle set and training set).

The sample

\[\tag{2} x^* = \argmax_{x \in D_{oracle}} s(x)\]

Is removed from \(D_{oracle}\) and labeled and added to \(D_{train}\).

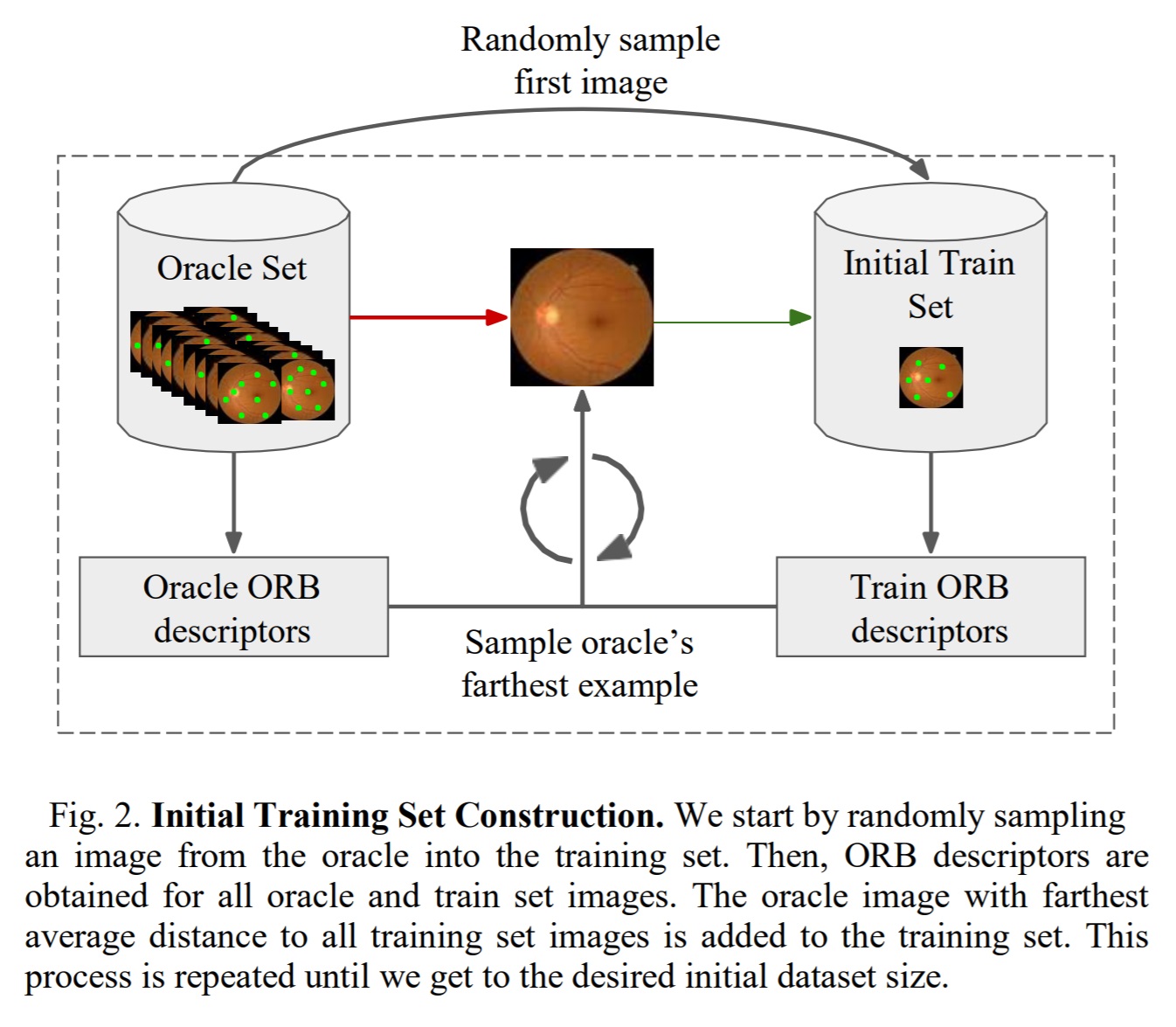
Initial train set construction

Standard active learning techniques label the first training set randomly as they require a trained model for evaluation uncertainty. The authors propose using Oriented FAST and Rotated BRIEF (OBR) descriptors to extract keypoints described by 256-bit vectors for each image.

The training set construction uses equations 1 and 2 to evaluate the images with the most information. The process is shown in Figure 2.

Implementation details

Authors use Inception V3 pre-trained on ImageNet and present results on 3 classification datasets:

Messidor Dataset (Diabetic Retinopathy classification)
Breast Cancer Diagnosis Dataset (ICIAR 2018 Grand Challenge)
Skin Cancer dataset

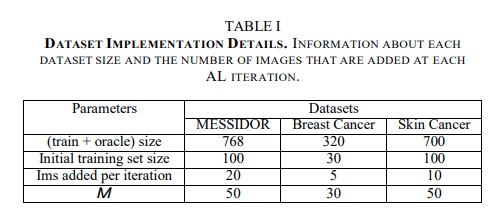
For each AL iteration, the model is trained from scratch to 100% accuracy on the training set.

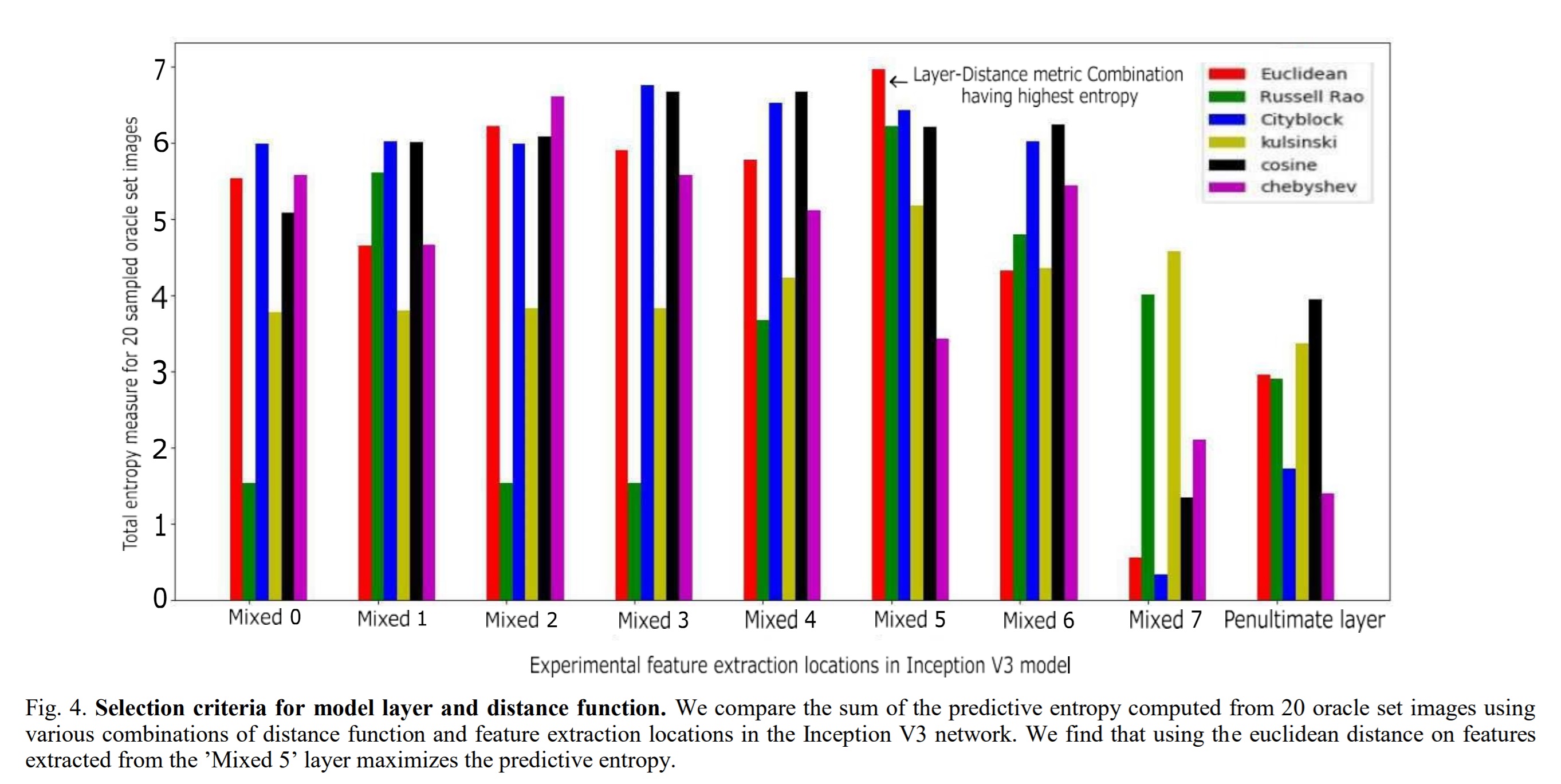
The authors consider different distance functions and different layers in the CNN to extract the most information. To select the best distance metric and layer the model was trained on Messidor’s initial training. For each distance metric and layer combination, 20 samples were selected from \(D_{oracle}\). The best combination is determined by the highest entropy for each selected sample.

Results

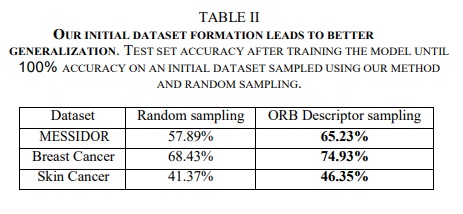
Initial train set construction results

The authors compare their method for selecting initial samples to random sampling. They train models until they reach 100% accuracy then evaluate on the test set.

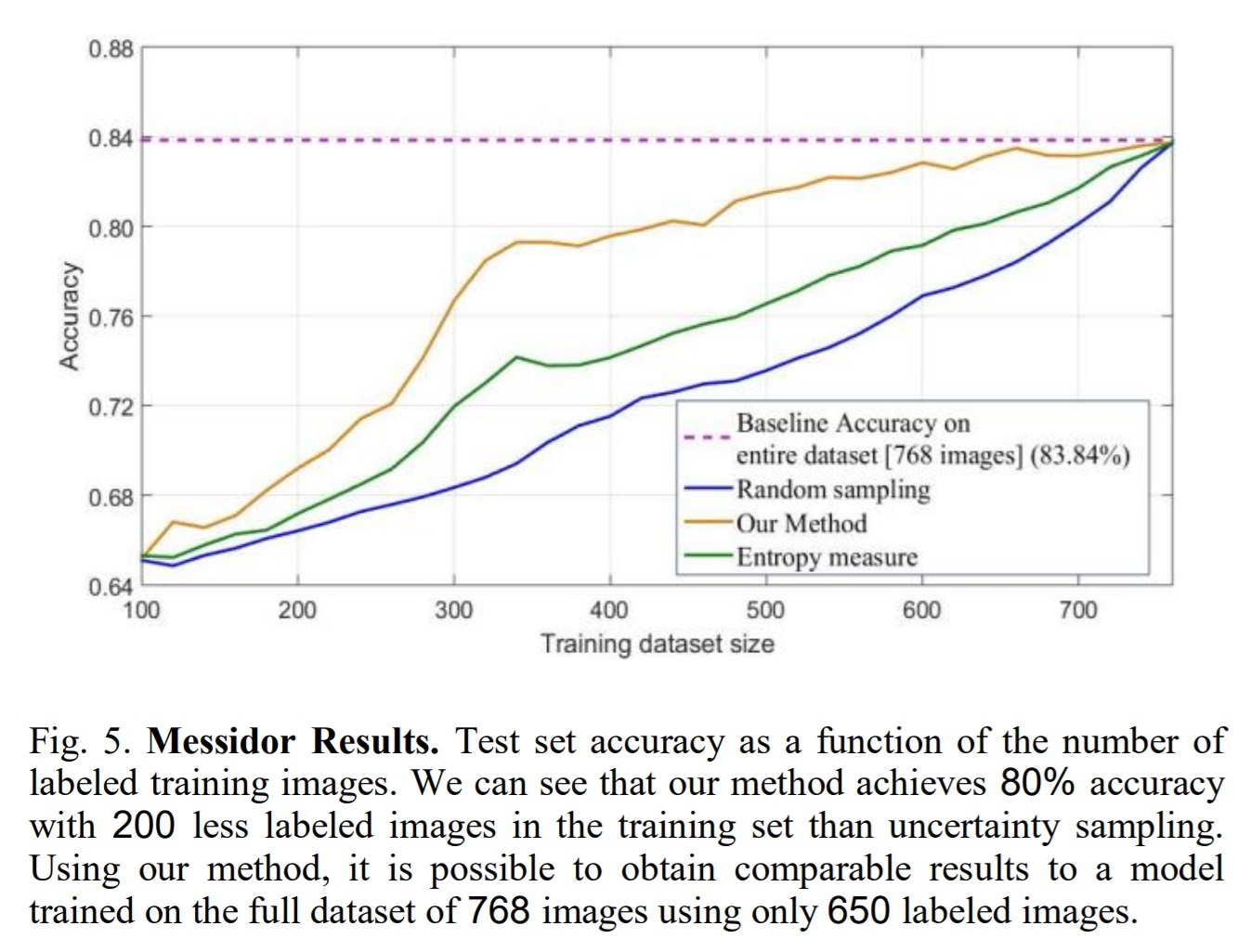
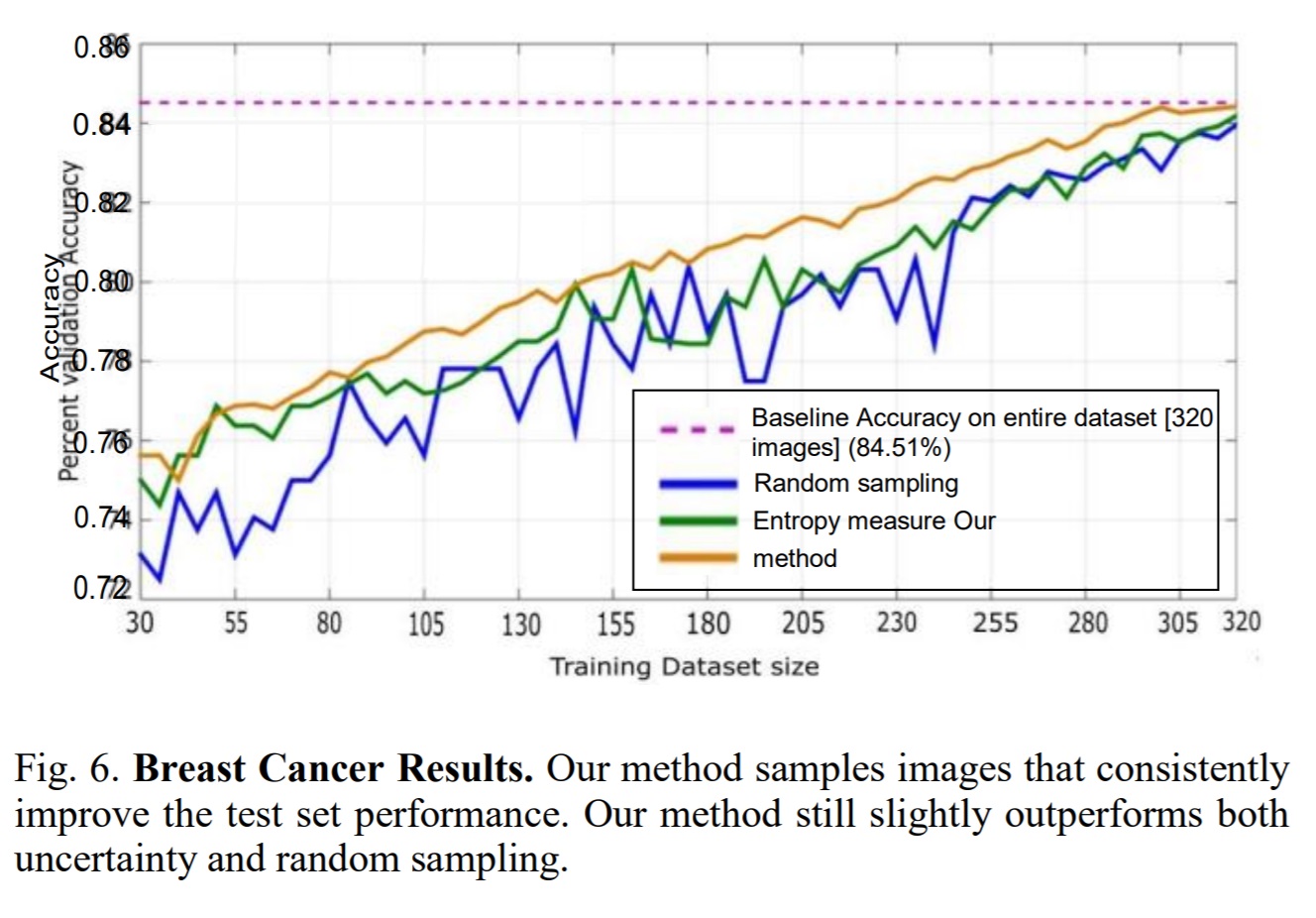
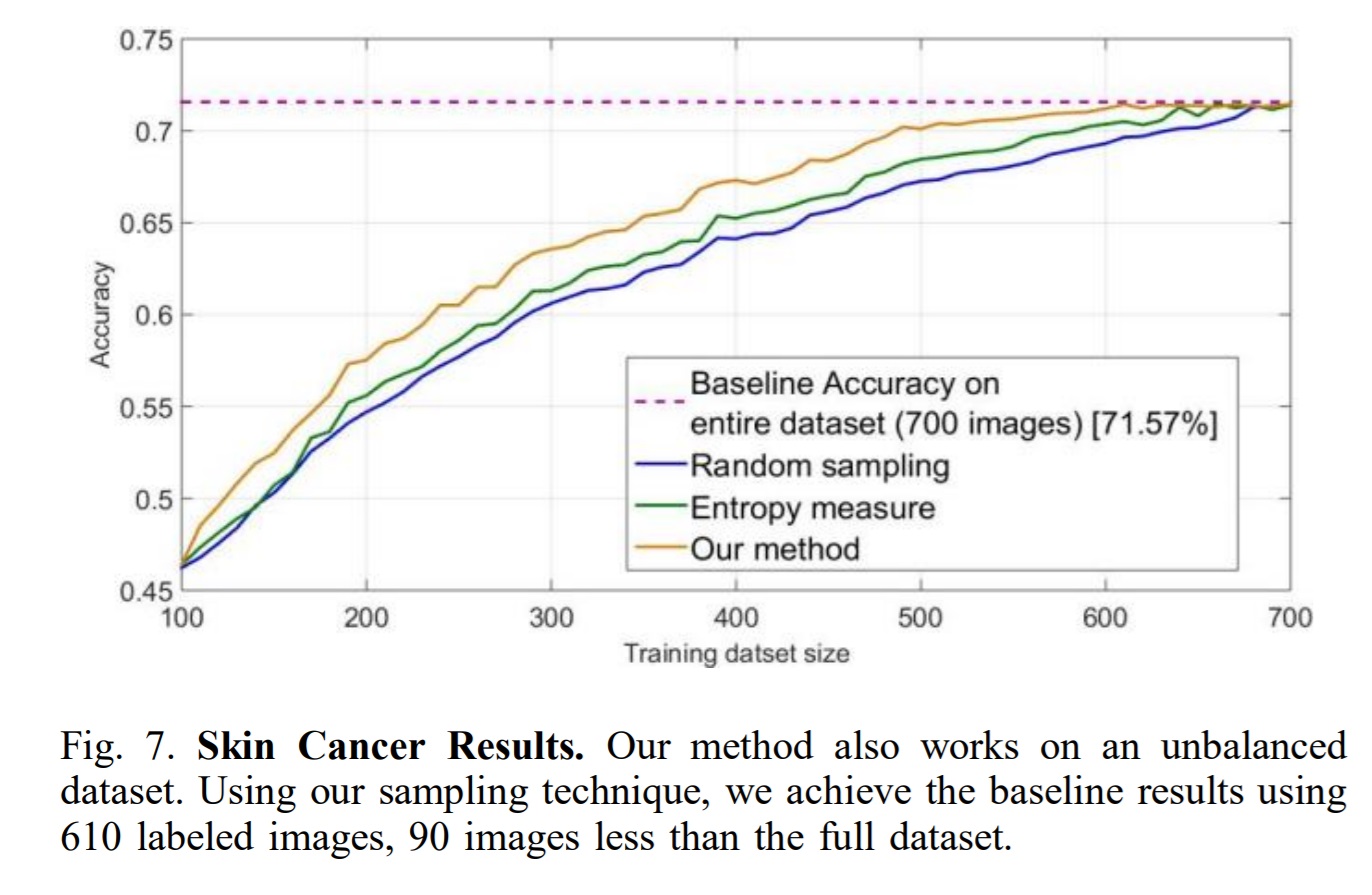
Active learning results

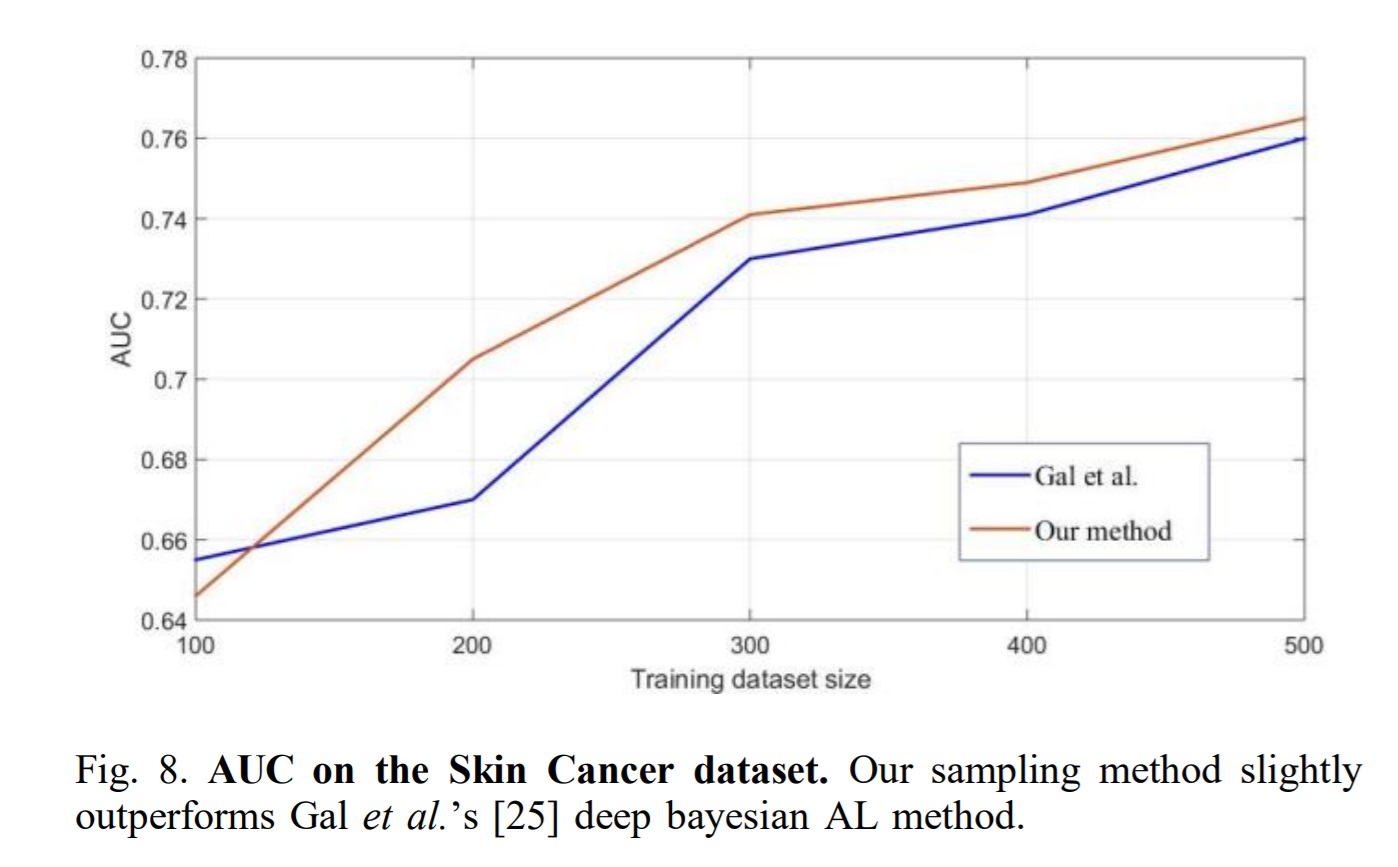
Conclusion

The authors present a novel way of sampling for active learning based on the representativeness of data points. Their method is better than entropy and random sampling but the results show only marginal improvements with respect to state of the art methods such as Gal et al.