Highlights

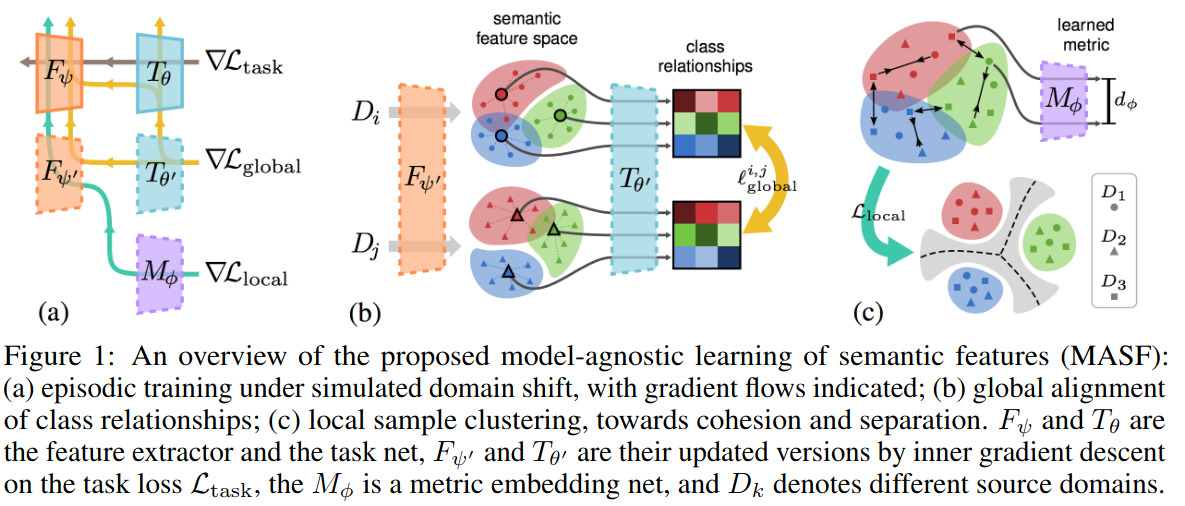
This paper proposes a new domain generalization method. The goal is for a model, trained on multi-domain source data, to generalize well on target domains with unknown statistics. The proposed system is illustrated in Figure 1.

Methods

Say we have various domains \(D=\{D_1,D_2,...,D_K\}\) and in each domain we have a series of labeled data \(D_k=\{(x_n^k,y_n^k)\}_{n=1}^{N_k}\). The proposed system comes with a feature extractor \(F_\phi\) and a task network \(T_\theta\). The predicted output for a given input \(x\) is \(\hat{y}=softmax(T_\theta(F_\phi(x)))\).

At each iteration, \(D\) is split into meta-train \(D_{tr}\) and meta-test \(D_{te}\) domains. Then, as shown in Figure 1, 3 losses are being optimised.

A task loss called \({\cal L}_{task}\) (a basic cross-entropy).
A global loss \({\cal L}_{global}\)
A local loss \({\cal L}_{local}\)

The goal of the global loss is to make sure that the class relationship is the same across domains. This is done by computing the average latent vector for every data associated to each class \(c\) and each domain \(k\)

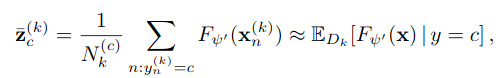
Then, take the average latent vector, decode it and compute its soft-cross-entropy

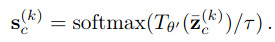
where \(\tau\) is a temperature term. The global loss is the following Jensen-Shannon divergence

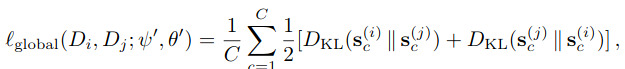
As for the local loss, its goal is to enforce that a latent vector is closer to another latent vector from the same class than one from from other classes. For this, they propose a contrastive loss or a triplet loss

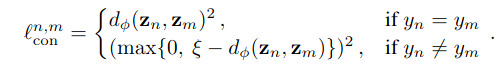
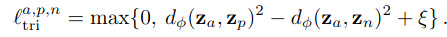
The overall training algorithm goes as follows

Results

The authors report good recognition accuracies on the PACS dataset (a dataset with challenging domain shift). Notice that DeepAll is their baseline for which all domains are merged and \(F_\phi.T_\theta\) is trained by standard supervised learning with \({\cal L}_{task}\). Interestingly, DeepAll beats several SOTA methods!

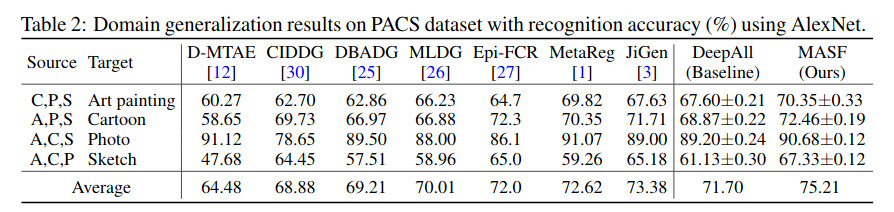
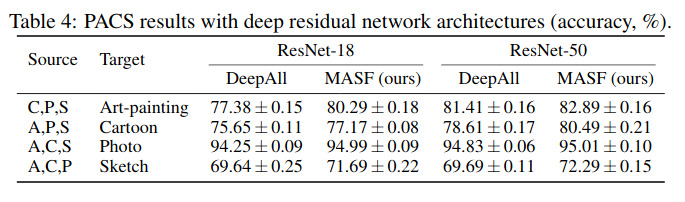
Unfortunately, their method does not seem to work better than naive DeepAll on medical images

Code is available here: https://github.com/biomedia-mira/masf