Highlights

In this paper, the authors study model scaling and identify that carefully balancing network depth, width, and resolution can lead to better performance.

They show that such balance can be achieved by scaling each of them with constant ratio. Based on this observation, they propose a simple compound scaling method which amounts to a simple neural architecture search.

Methods

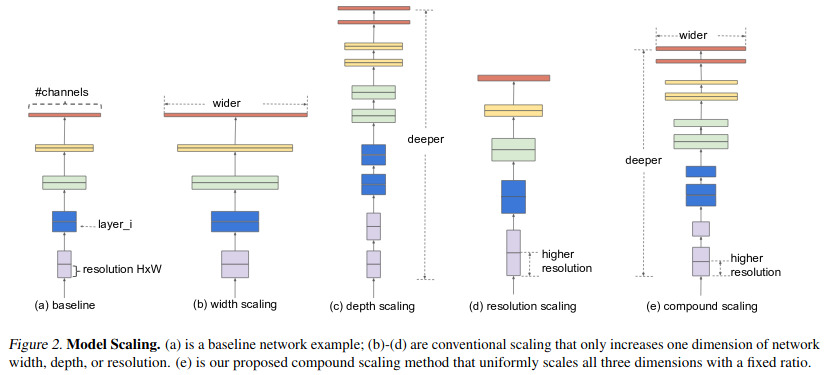
The authors consider the following three elements of a neural network (c.f.Fig.2):

  • Depth: the number of layers.
  • Width: the number of neurons (and feature maps) at each layer
  • resolution : the size of the input image.

Acknowledging the fact that these variables are somehow connected to each other (e.g in a ConvNet, increasing resolution will affect the depth) they propose the following compound coefficient \(\phi\)

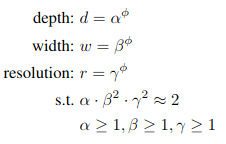
This leads to their simple neural architecture search algorithm namely:

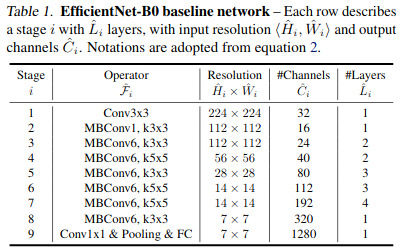
where the baseline network is this

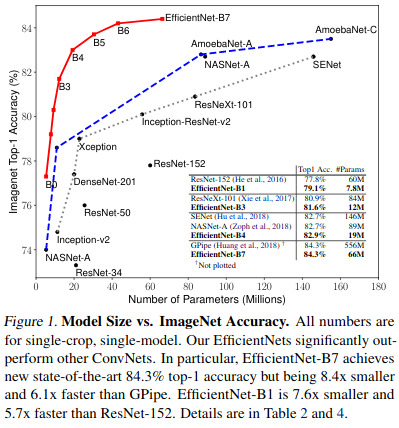
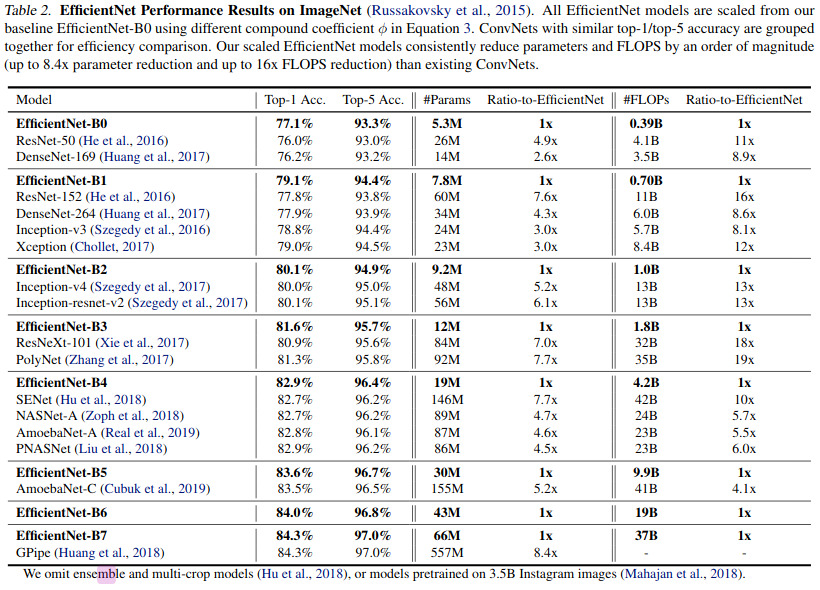
Results

Results are pretty convincing!

References