Highlights

Authors propose a Variational Autoencoder (VAE) that uses an Adaptive Clustering (AC) strategy to improve the classification performance of \(k\)-NN-based VAE classification methods.
The AC-VAE strategy is a self-supervised method that does not require to adapt any hyper-parameter (such as \(k\) in k-NN) for different classification contexts.

Introduction

Unsupervised representation learning methods offer a way to leverage existing unlabeled datasets. Representation learning acts as a feature extractor step that is later used by downstream strategies to assign labels to previously unlabeled data. \(k\)-NN is a popular choice to classify data points within such a context using the available neighboring data point labels. However, the right choice of the \(k\) parameter is problem-dependent and not evident, and authors state it as a major drawback for some state-of-the-art methods.

Similarly, authors argue that pretext tasks used to learn the representations with the aim of using them in downstream tasks (such as clustering) are not geared towards explicitly improving the clustering ability.

Authors propose a strategy named Adaptive Clustering Variational Autoencoder (AC-VAE) to overcome the difficulty of choosing the appropriate \(k\) parameter. VAEs are usually trained to reconstruct the input signal (and minimize the latent distribution wrt a prior assumed distribution) and the learned low-level features may not be the most appropriate ones for semantic classification tasks. Authors propose to solve the classification task using the z-scores computed from the latent space distributions of the VAE.

Methods

The proposed method consists of two stages

A generative network that produces the representation and its boundary information.
A clustering method that benefits from the boundary information computed in the previous step.

The distribution’s mean \(\mu\) is taken as the representation; meanwhile, its z-score provides the boundary information that can naturally adapt to different datasets. The proposed clustering method takes advantage of the boundary information to achieve adaptive neighbor clustering.

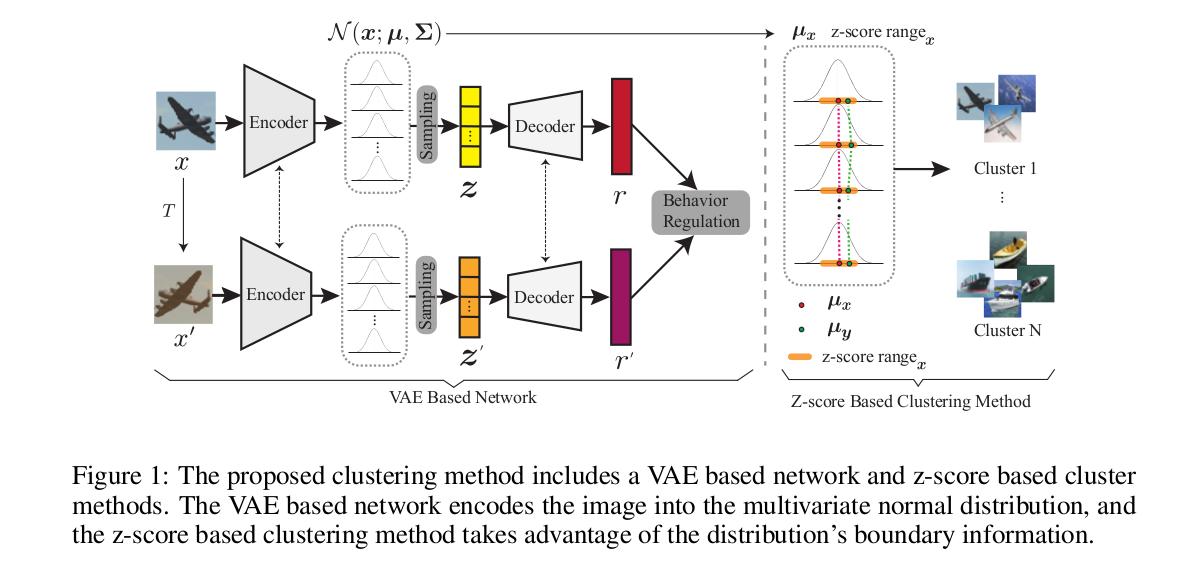
The generative network is a modified VAE, where the mean of the distribution approximated by the encoder is added to the sampled latent vector prior to the decoder block, which generates a “representation”.

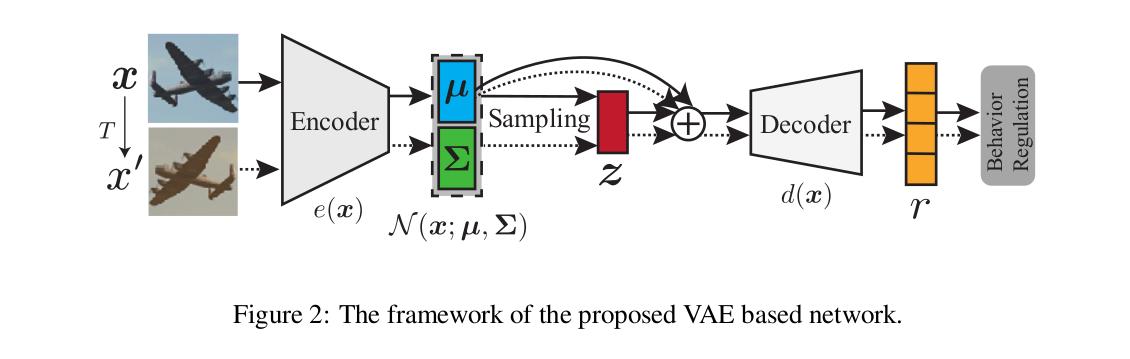
The network is trained by “behavior regulation”, i.e. minimizing the behavior loss between an input image representation and an augmented version of the same input image.

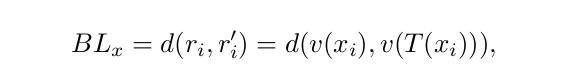
So the image reconstruction term in the traditional VAE loss function is substituted by the behavior loss.

As mentioned earlier, the latent distribution will act as a close approximation of the desired representation. The mean μ will be regarded as the image representation, and the z-score of the distribution characterizes its boundary information.

The clustering method works on the assumption that:

This work clusters the images based on the boundary information based on z-score. The insight is that, when an image is encoded into the distribution, the image’s close variations should be located within a small z-score range of this distribution.

For neighbor clustering, the neighbor whose means \(\mu\) fall into the required z-score ranges (controlled by the clustering range parameter \(\alpha\)) will be clustered. A loose match strategy by means of a single parameter \(\theta\) allows the clustering method some flexibility with respect to a strict z-score requirement.

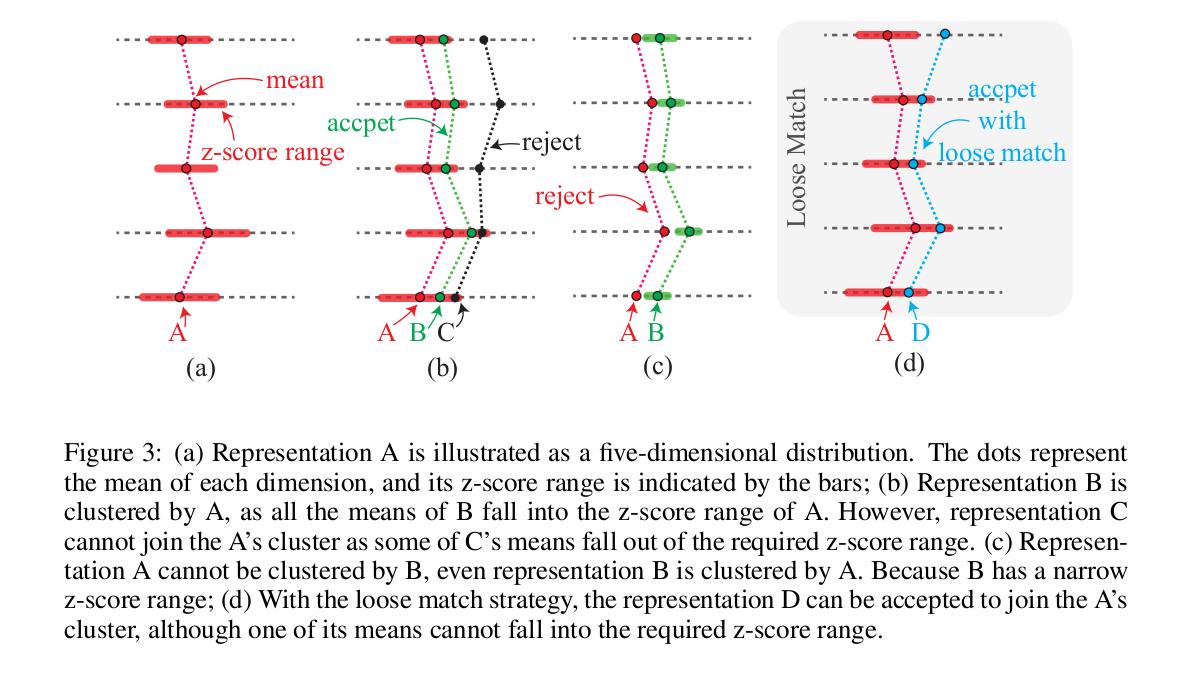
Authors argue that this framework makes the method not to depend on any might-be problem-dependent parameter:

As the experiment in section 4 will demonstrate, cluster converging after \(\alpha\) surpasses a certain value are observed on all evaluated datasets, so the \(\alpha\) needs no fine-tuning for each dataset.

In practice, there is no need to fine-select \(\alpha\) nor \(\theta\) to reach a specific cluster size unless a particular representation falls into the boundary. As the representation is a high dimensional distribution, neighbor cluster size is highly desired.

Authors use a ResNet-34 network as the encoder, and a two-layer full connection as the decoder network, providing a 64-dimensional representation vector at its output. The latent space dimensionality is fixed to 512.

It is unclear why authors say that the output of the decoder has a size of 64, given that none of the datasets used fits into that size, neither from the point of view of the image nor from the point of view of the number of classes.

Data

CIFAR10, CIFAR100-20 and STL10.

Results

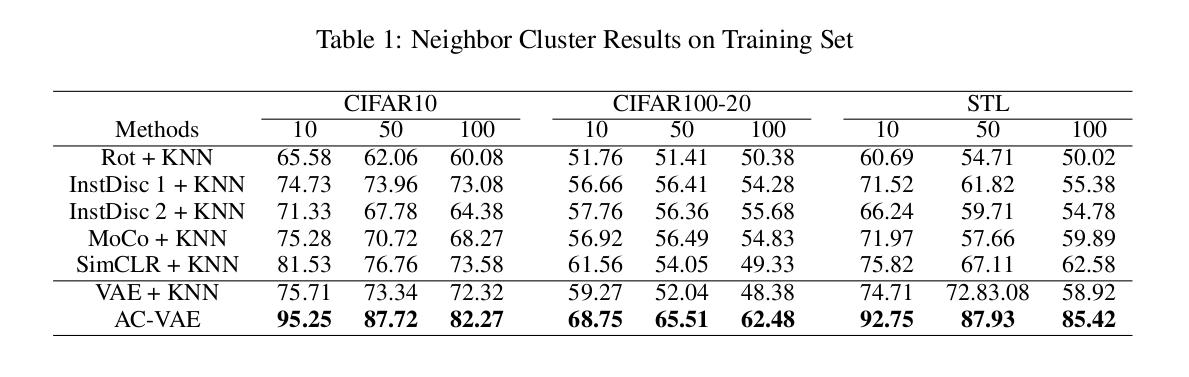
Authors compare their method to a number of baselines that use a k-NN strategy for classifying the input data. They also include as a baseline their VAE network using k-NN.

Their proposed method outperforms the baselines by a considerable margin for the given cluster sizes: AC-VAE achieves between 95% and 82% accuracy on CIFAR10 when the neighbor cluster sizes are 10 and 100.

Conclusions

Authors present a method to perform clustering based on a VAE that looks to explicitly minimize the distance of the semantic representations of the input data, and the boundary informations retrieved from this distribution.

Authors affirm that their methods achieve state-of-the-art clustering performance when omitting a critical super-parameter \(k\) in the state-of-the-art method.

Comments

Authors do not explain how the augmentation is determined to train the network driven by the behavior loss.
Their results Table 1 reports results from the training set.