Phasic Policy Gradient
Highlights
- More sample-efficient actor-critic reinforcement learning algorithm
Introduction
Most policy gradient (PG) reinforcement learning (RL) algorithms use the Actor-Critic (AC) framework. In this context, two neural networks are trained in parallel: one being the Actor, aka the policy, which outputs actions that are applied to the environment and the second network being the Critic, which infers the value of the actions output by the actor. By using the training signal provided by the critic, the actor can learn more efficiently.
Whether or not the actor and the critic share parameters is usually a pretty big choice to make: If parameters are shared, features learned by one of the networks can be reused by the other. However, it also means that both networks’ objectives might interfere with each other. The authors also argue that this forces the networks to be trained on the same data, and therefore impose the same level of sample reuse, which might be undesirable. On the other, having two separate networks means that they cannot share learned features.
To try and have the best of both worlds, the authors propose the Phasic Policy Gradient algorithm, where feature sharing is kept but the two networks training are decoupled.
Methods
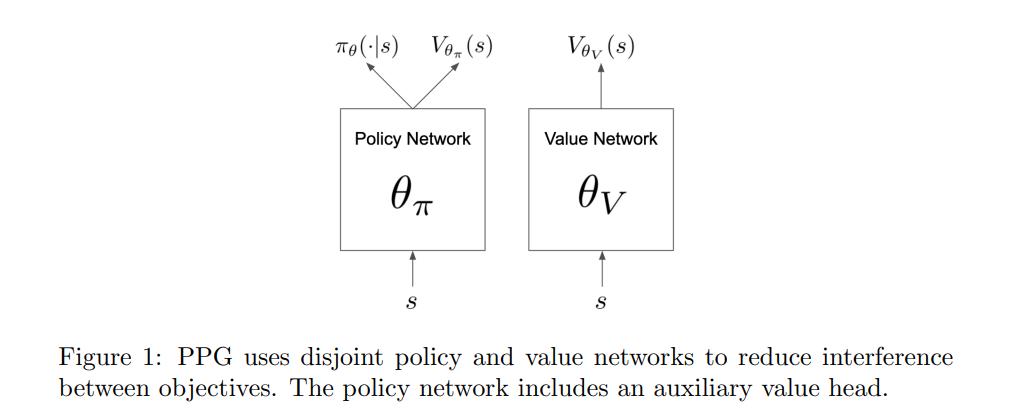
To decouple training while also enabling feature sharing, a novel actor-critic architecture is proposed where the actor and critic use separate networks, while also adding a critic head to the actor network. Figure 1 highlights the proposed architecture.
To train the networks, the learning process is split into two phases: The policy phase and the auxiliary phase. During the policy phase, the actor is trained using the standard PPO1 clipped loss:
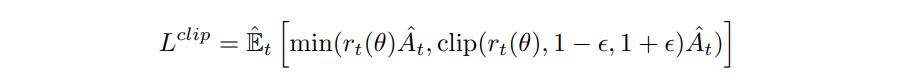
where \(r_t(\theta) = \frac{\pi_\theta(a_t{\mid}s_t)}{\pi_{\theta_{old}}(a_t{\mid}s_t)}\). During the same phase, the critic is also trained using standard \(L_2\) loss
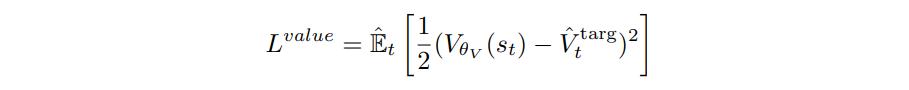
where \(\hat{V}^{targ}_t\) and \(\hat{A}_t\) are computed with GAE2. The policy phase so far is on par with previous works. The novelty comes from the auxiliary phase, where the policy is again optimized, but this time with the following joint loss:
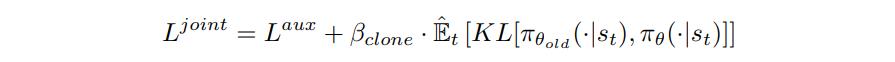
which includes an auxiliary loss \(L^{aux}\) component for the auxiliary critic head on the actor network, as well as a behavioral cloning loss component to preserve the original policy. \(\pi_{\theta_{old}}\) is the policy right before the auxiliary phase begins.
\(L^{aux}\) is again a \(L_2\) loss
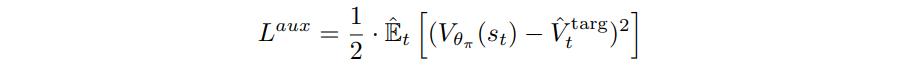
where \(\hat{V}^{targ}_t\) are the targets computed during the policy phase and \(V_{\theta_\pi}\) is the critic head shown in Figure 1.
The whole algorithm is shown below:

Data
The algorithm was tested on the Procgen Benchmark suite3.
Results
Comparison to PPO
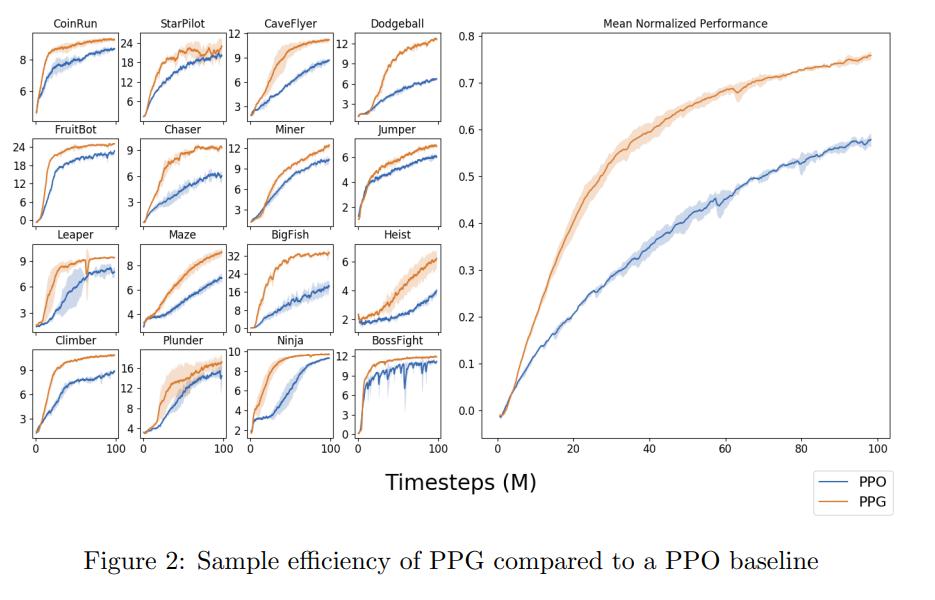
We can see that the algorithm learns faster as well as better than PPO on all environments.
Sample reuse
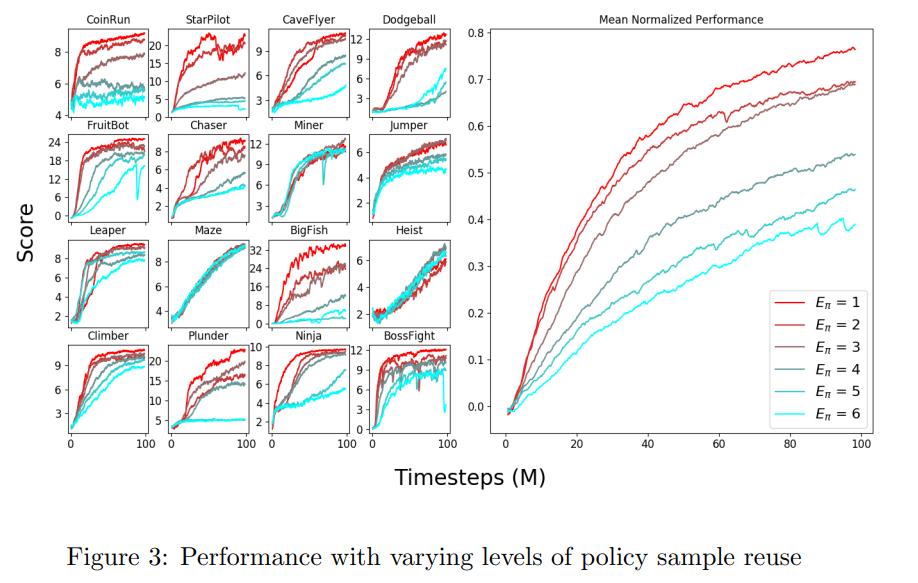
Reusing the same samples for multiple training epochs for the policy does not seem to improve performance.
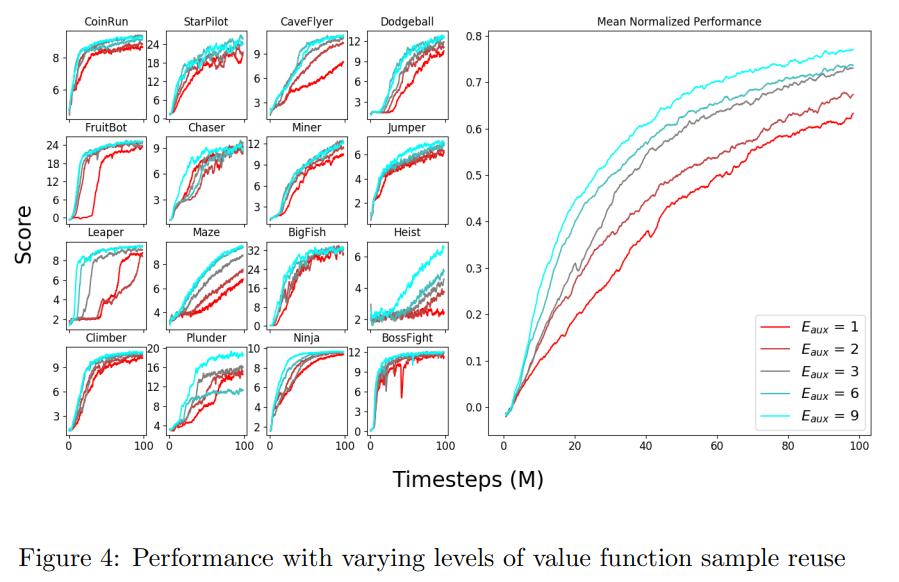
We find that training with additional auxiliary epochs is generally beneficial, with performance tapering off around 6 auxiliary epochs.
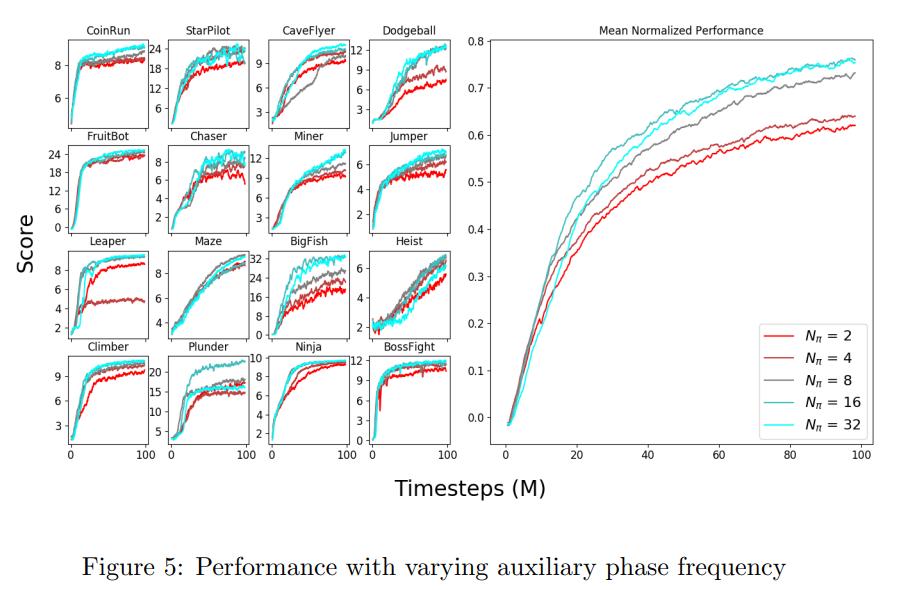
It is clear that performance suffers when we perform auxiliary phases too frequently. We conjecture that each auxiliary phase interferes with policy optimization and that performing frequent auxiliary phases exacerbates this effect.
Single network vs. multiple networks
Having multiple networks instead of a single one means a higher memory requirement and more computing power is needed. The authors therefore try to merge the architecture in Fig. 1 and report results:
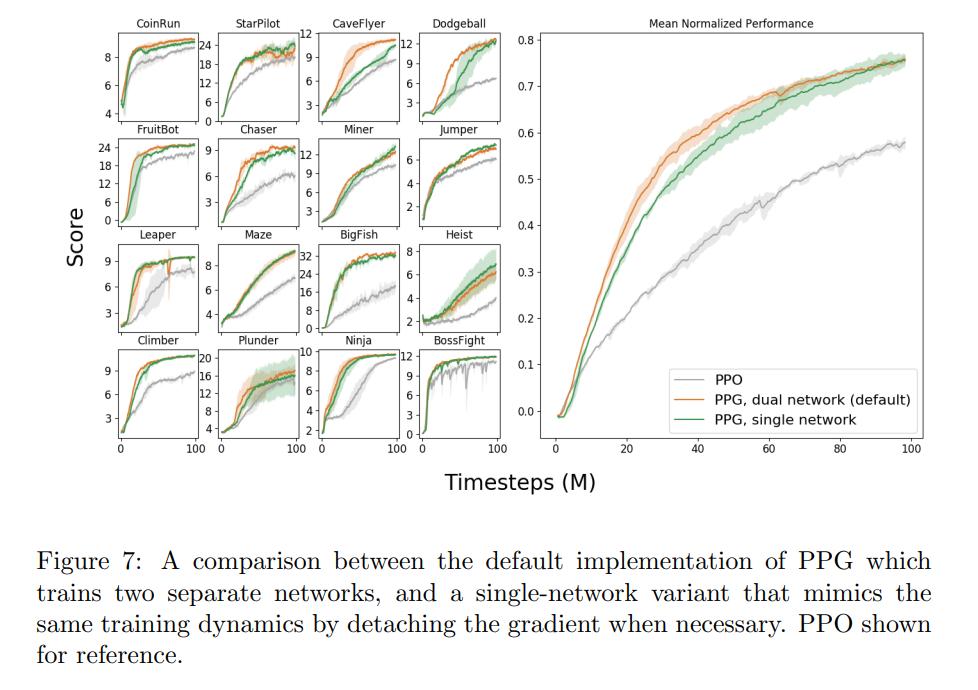
To make sure that the loss for the critic does not influence the actor, the value function gradient is detached at the last layer shared between the actor and the critic during the policy phase.
As we can see, using PPG with this single shared network performs almost as well as PPG with a dual network architecture. We were initially concerned that the value function might be unable to train well during the policy phase with the detached gradient, but in practice this does not appear to be a major problem. We believe this is because the value function can still train from the full gradient during the auxiliary phase.
Conclusions
By mitigating interference between the policy and the value function while still maintaining the benefits of shared representations, PPG significantly improves sample efficiency on the challenging Procgen Benchmark. Moreover, PPG establishes a framework for optimizing arbitrary auxiliary losses alongside RL training in a stable manner
Remarks
- Would have been nice to see results on the Mujoco or Atari suite