Highlights

Use of positive homogeneity (or positive scale invariance) of ReLU networks to suggest an optimization method that is invariant under rescaling of the weights.
This is done with respect to a path regularizer.

Introduction

Stochastic gradient descent and its variants are not invariant under rescaling by positive factors. This means that two ReLU networks whose weights are equivalent via positive homogeneity have different descent paths.

Notation

A feedforward neural network computes a function \(f: R^D \to R^C\) and can be represented by a directed acyclic graph G with set of vertices V and edges E, with D input nodes \(v_{in}[1],...,v_{in}[D]\) and C output nodes \(v_{out}[1],...,v_{out}[C]\). Denote the weight from vertex \(u_1\) to \(u_2\) by \(w_{(u_1 \to u_2)}\). When the oriented graph of the network is \(G\) the network function with respect to the weights \(w\) and the activation \(\sigma\) is denoted \(f_{G,w,\sigma}\). In this paper they focus in the case where \(\sigma\) is the ReLU activation.

Rescaling and Unbalanceness

Given a positive scalar \(c \geq 0\) we have \(ReLU(cx) = cReLU(x)\) for any real number \(x\). For a positive scalar \(c\) and a node \(v\) the rescaling function \(\rho_{c,v}\) multiplies the incoming weights to node \(v\) by \(c\) and the outgoing weights by \(1/c\). So \(\rho_{c,v}(w)=\widetilde{w}\) where

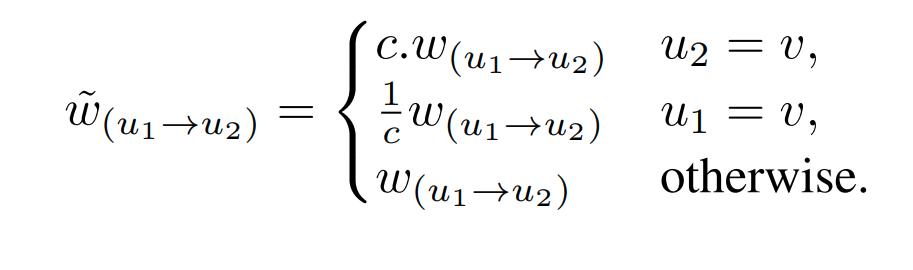
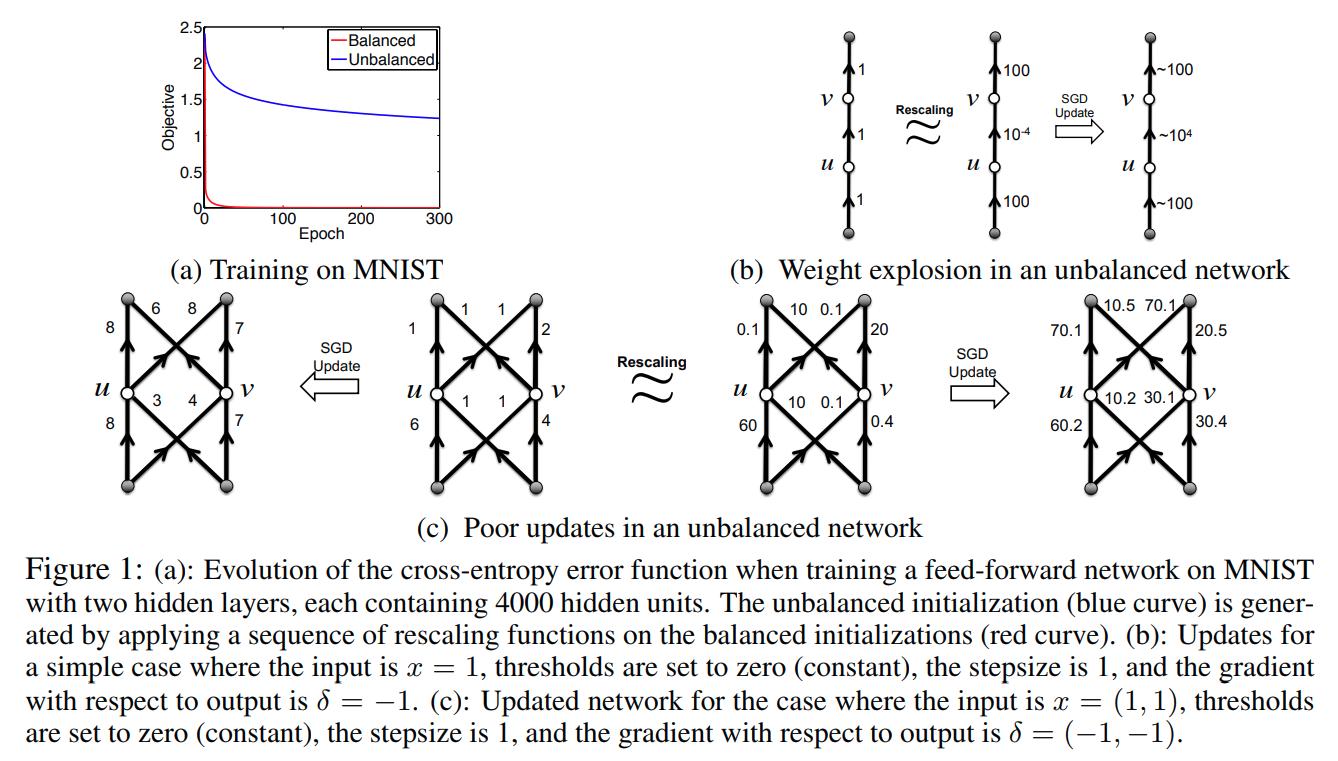
One has that \(f_{G,w,\sigma} = f_{G,\widetilde{w},\sigma}\). The authors call an optimization method rescaling invariant if the updates of rescaled networks are identical. Clearly, see Fig 1 (c), gradient descent is not rescaling invariant.

Even more, gradient descent performs very poorly on unbalanced networks. Where balanced means that the norm of the incoming weights to different units are roughly the same within a small range.

Magnitude/scale measures for deep networks

The following is a general type of regularizer

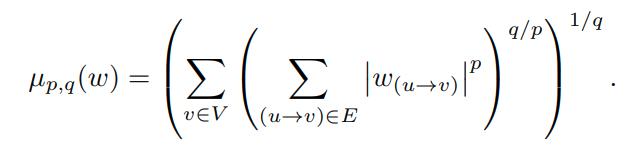
For example, p=q=1 gives \(\ell_1\) regularization and p=q=2 gives \(\ell_2\) regularization, also known as weight decay. And in case q=\(\infty\) this can be written as:

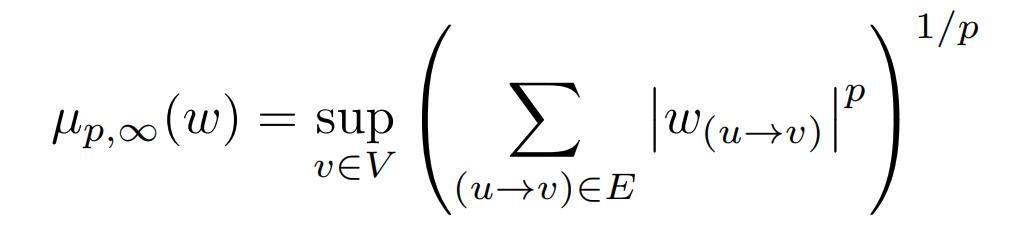
Denote \(\pi(w)\) the path vector, that is, the number of coordinates of \(\pi(w)\) is equal to the number of paths in the graph G from every input node to every output node, and each coordinate of it is equal to the product of the weights along the corresponding such path. The authors define the \(\ell_p\) path regularizer as the \(\ell_p\) norm of \(\pi(w)\):

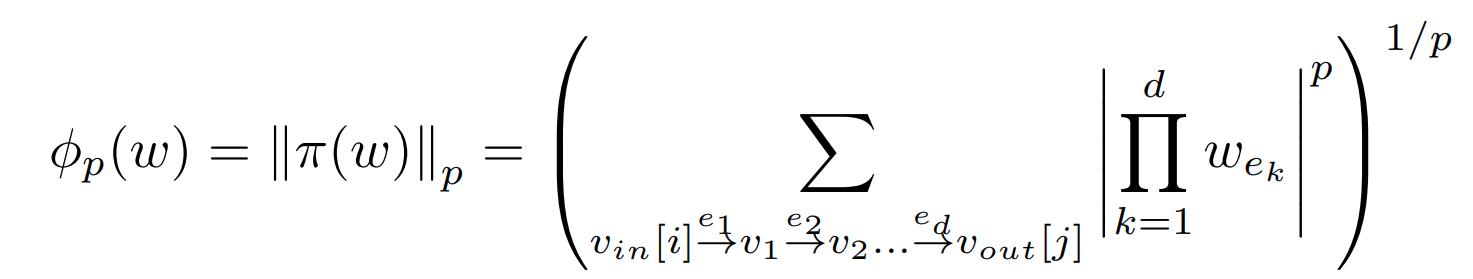
They use the following lemma (from one of their references):

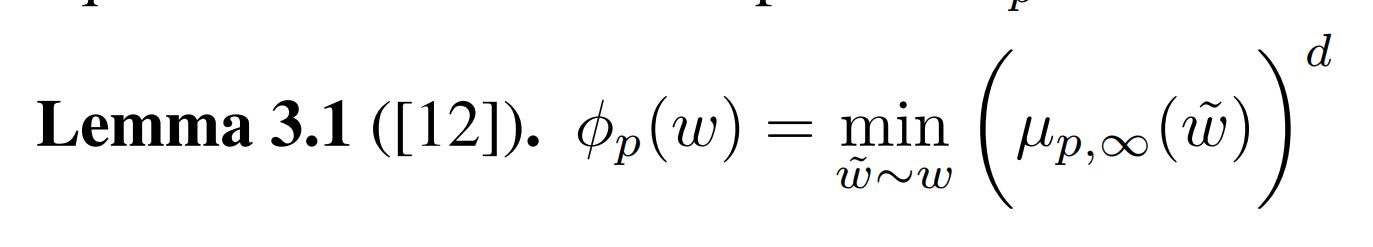
They show that, using dynamic programming, \(\phi_p(w)\) can be computed in a single forward pass using the following formula (even though the number of coordinates of \(\pi(w)\) grows exponentially).

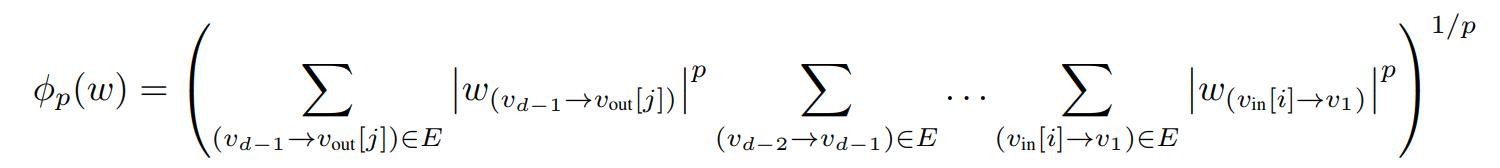
Path SGD

The authors derive a descent direction with respect to the path regularizer \(\phi_p(w)\) as follows:

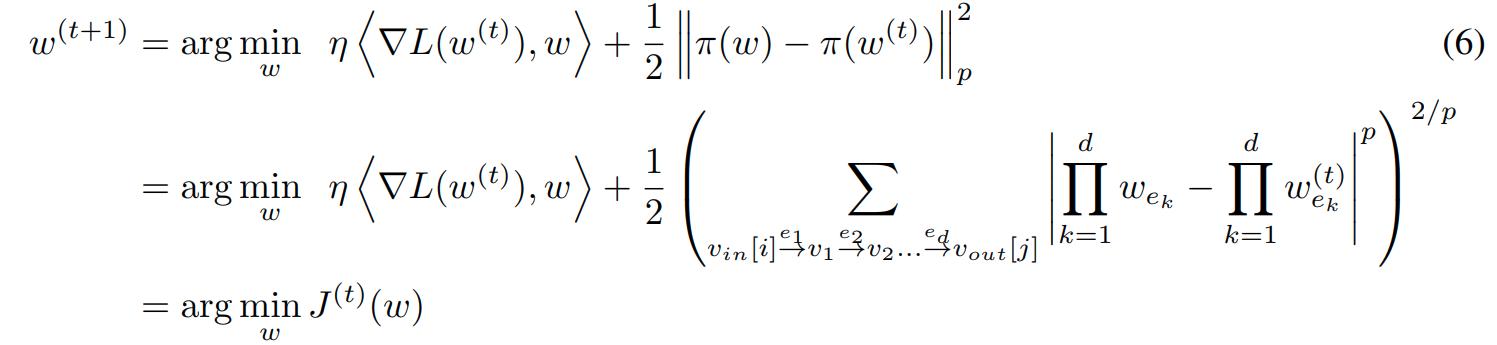
The first line is hard to calculate exactly, so they update each weight \(w_e\) as

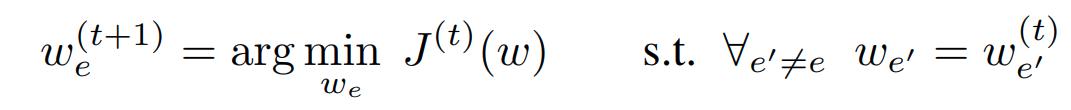
Then taking the derivative and setting it to zero:

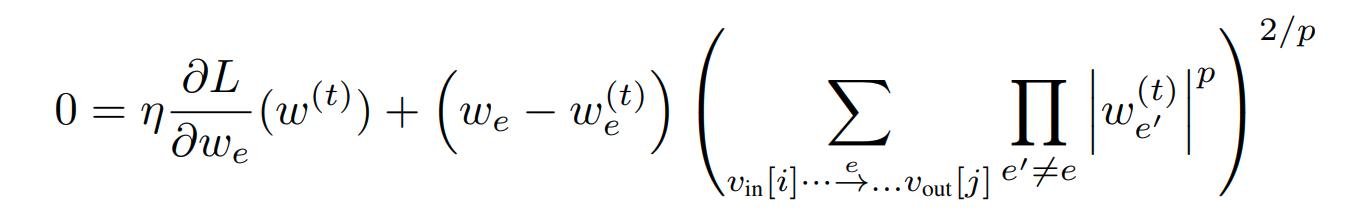
Solving for \(w_e\) gives the update rule:

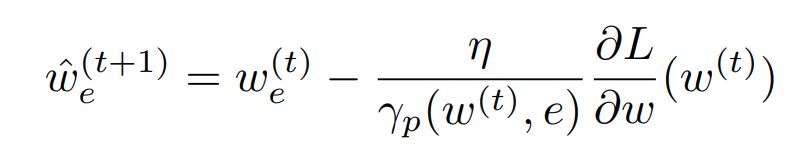
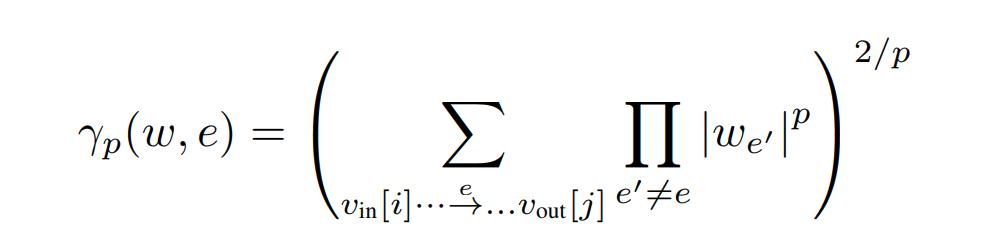
The authors claim this implementation is efficient in the sense that if B is the size of a mini batch and the backpropagation on the mini batch can be done in time BT, then Path-SGD on the mini batch will be B(T+1).

Experiments

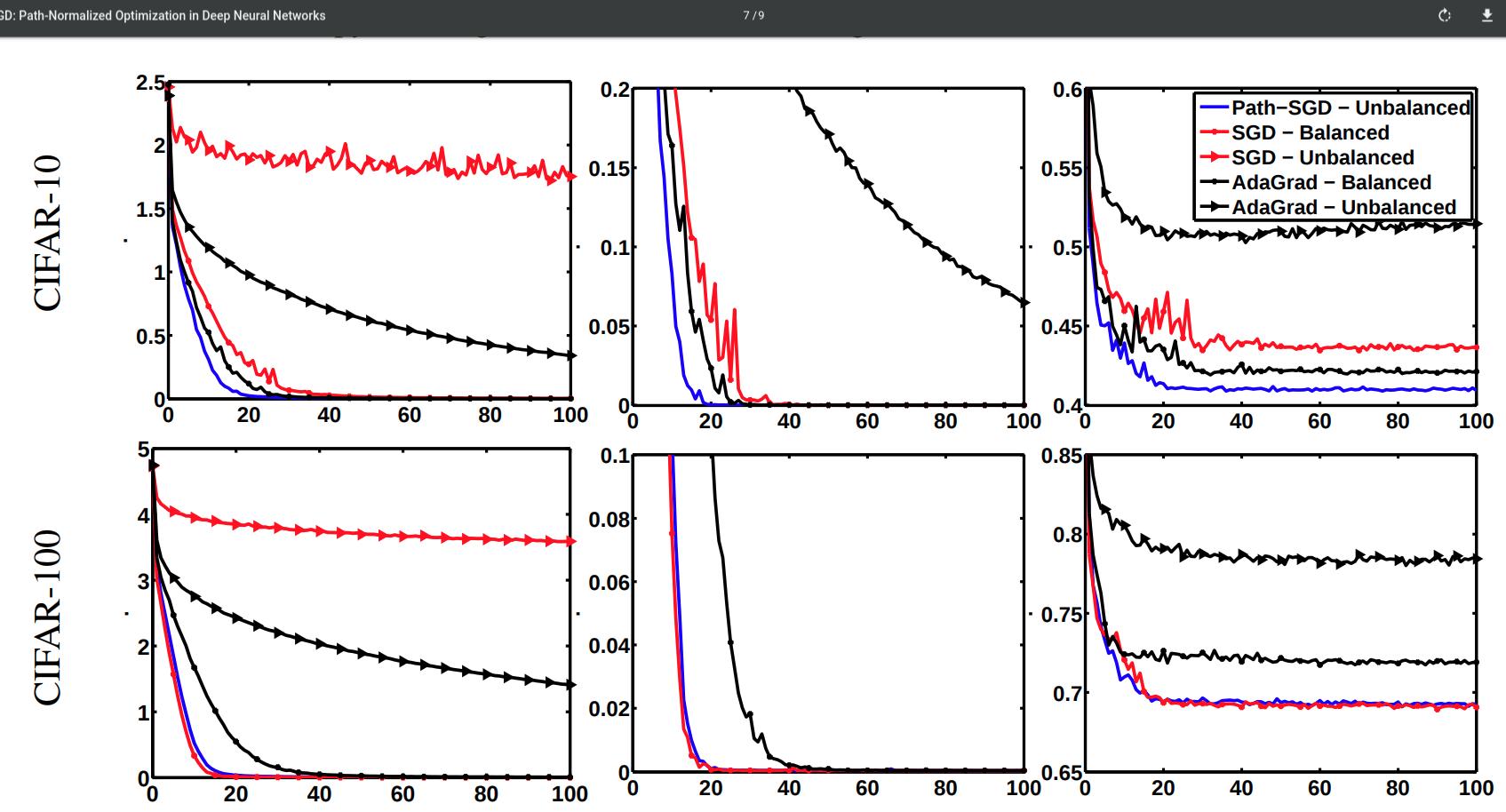
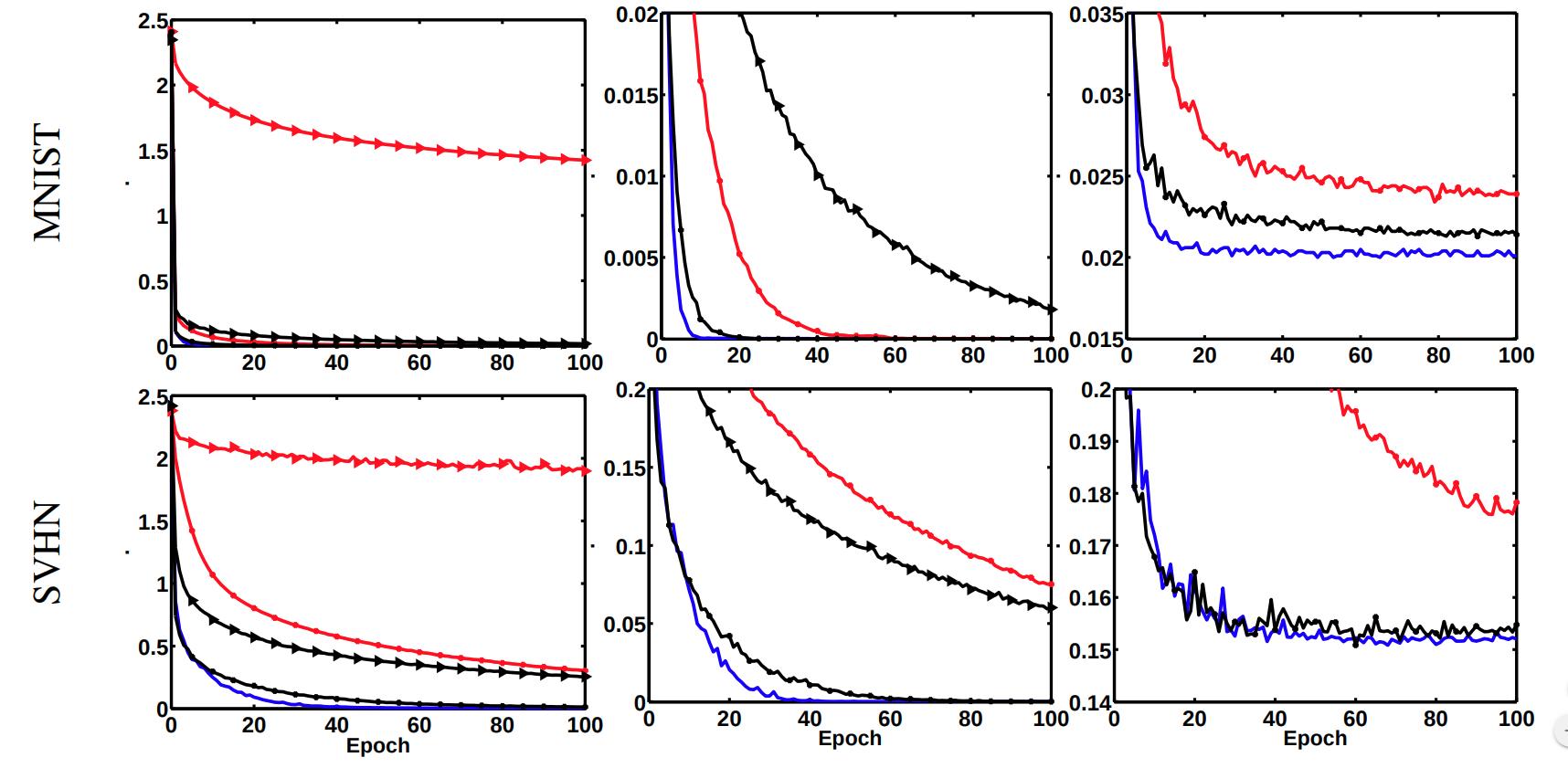
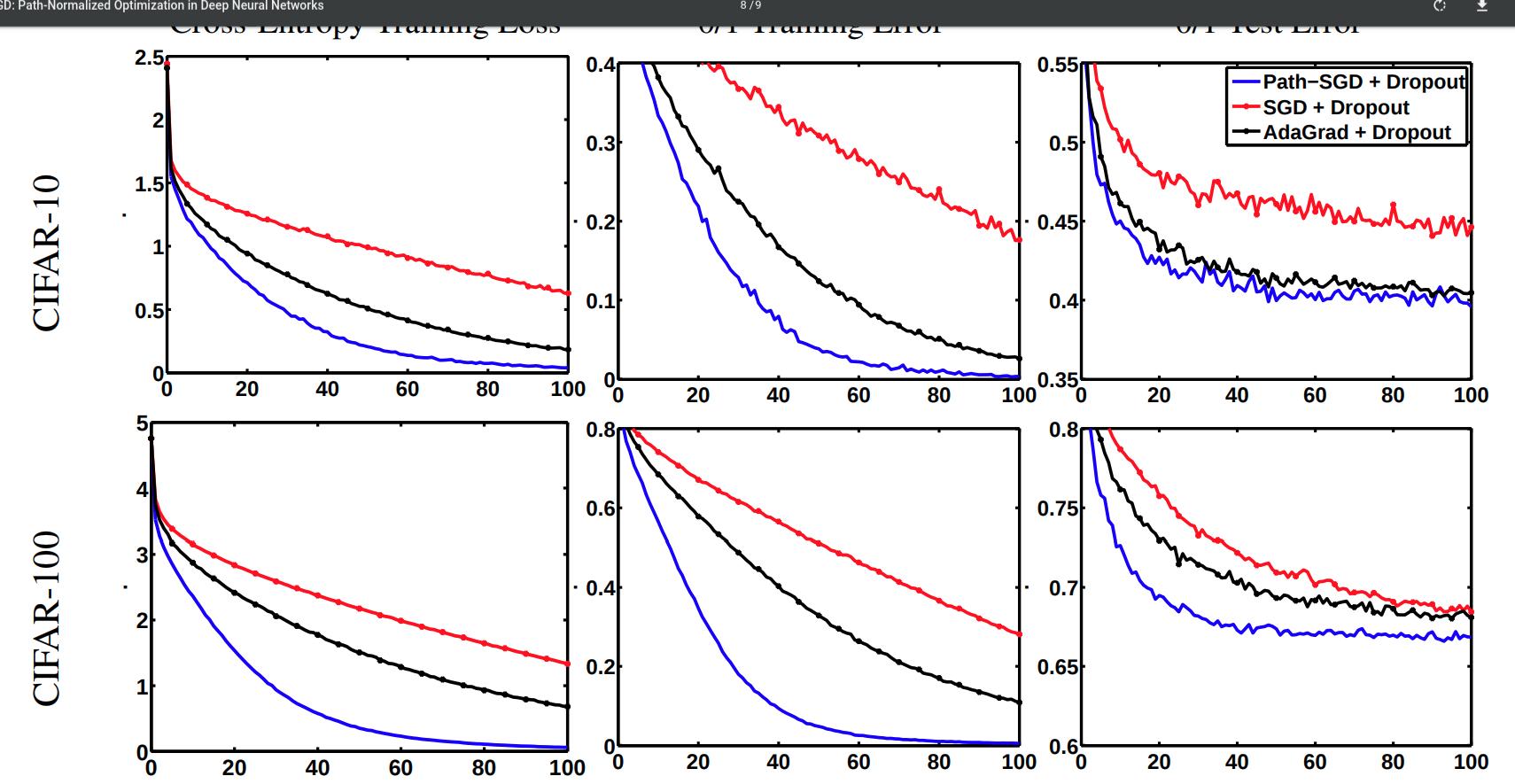
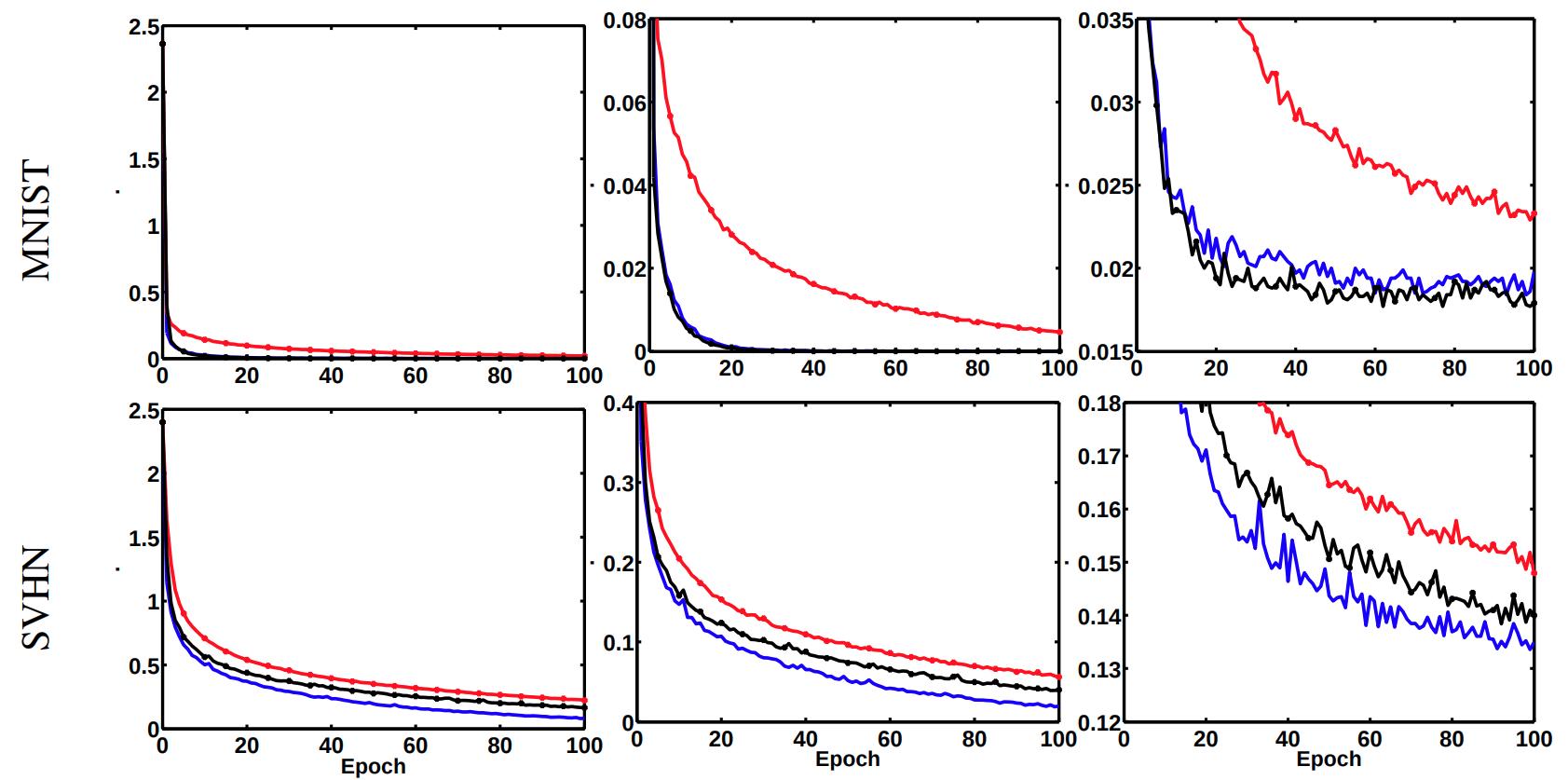
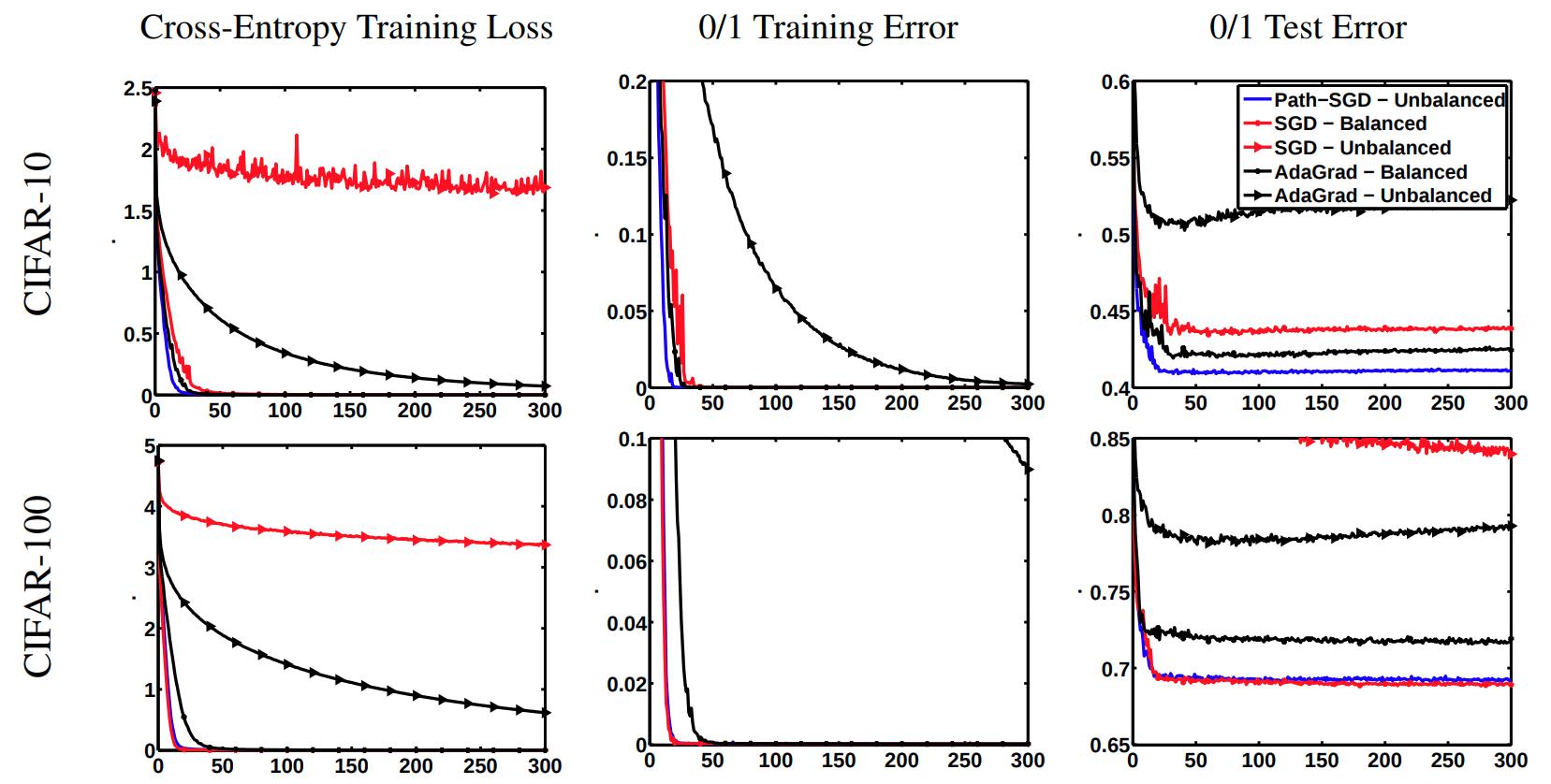
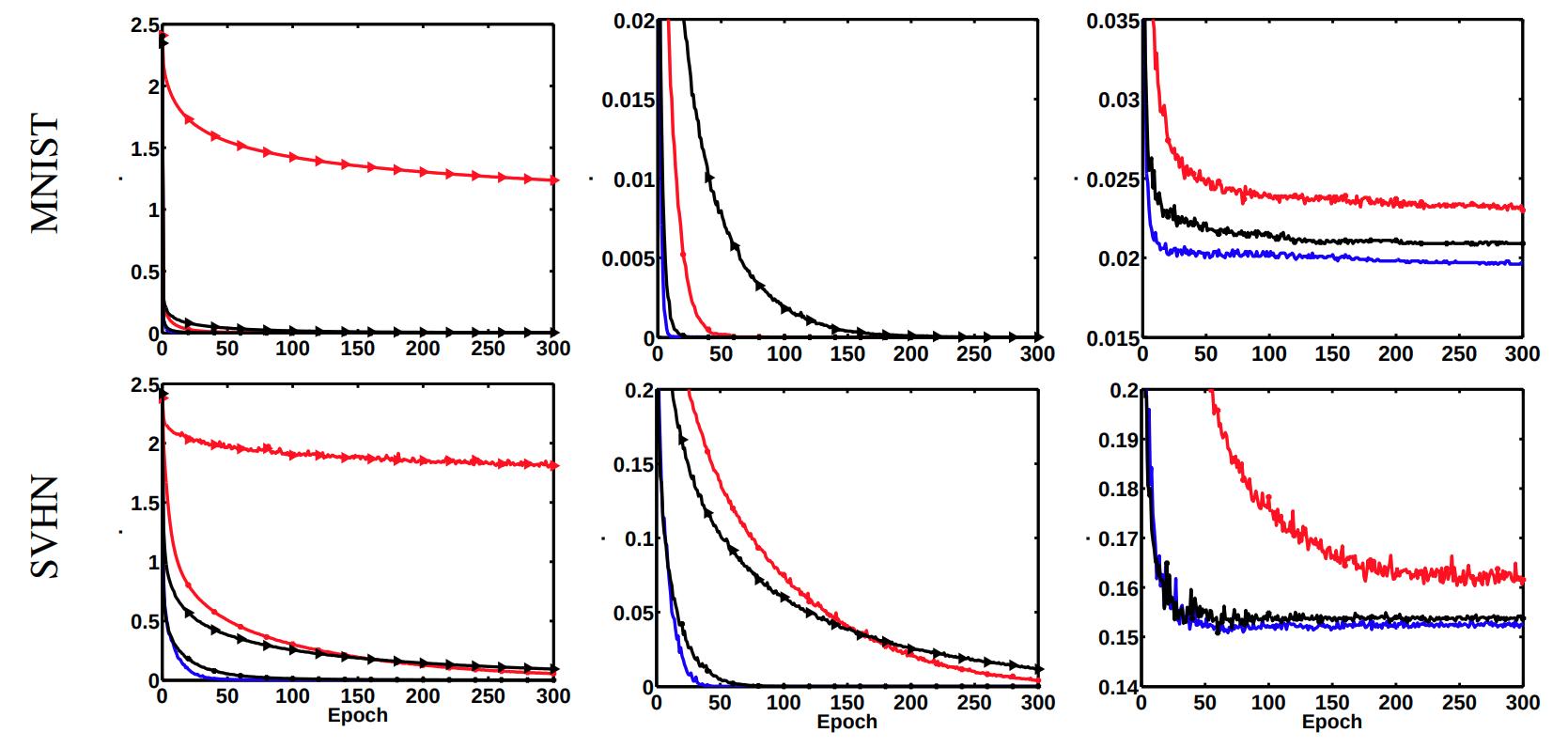
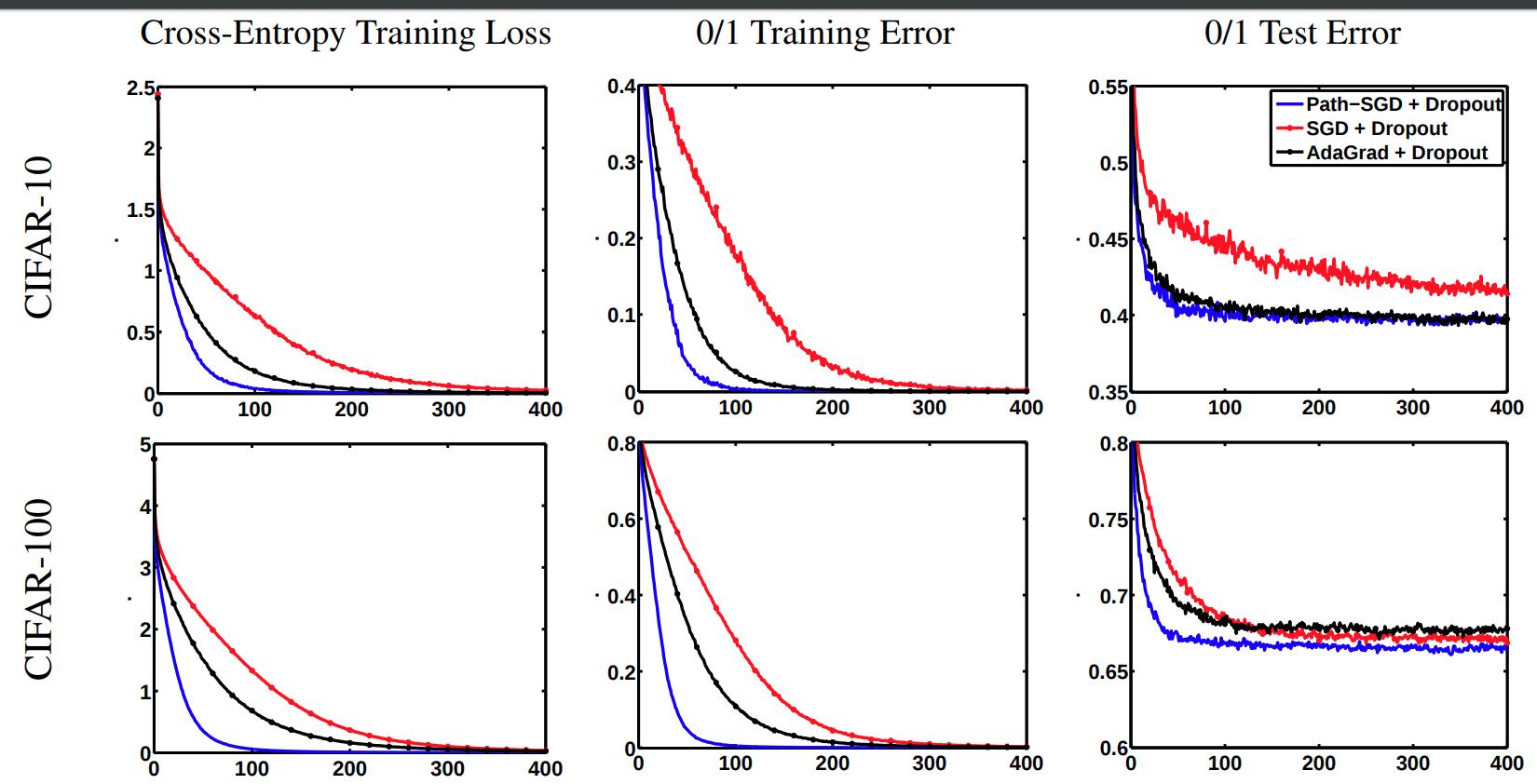
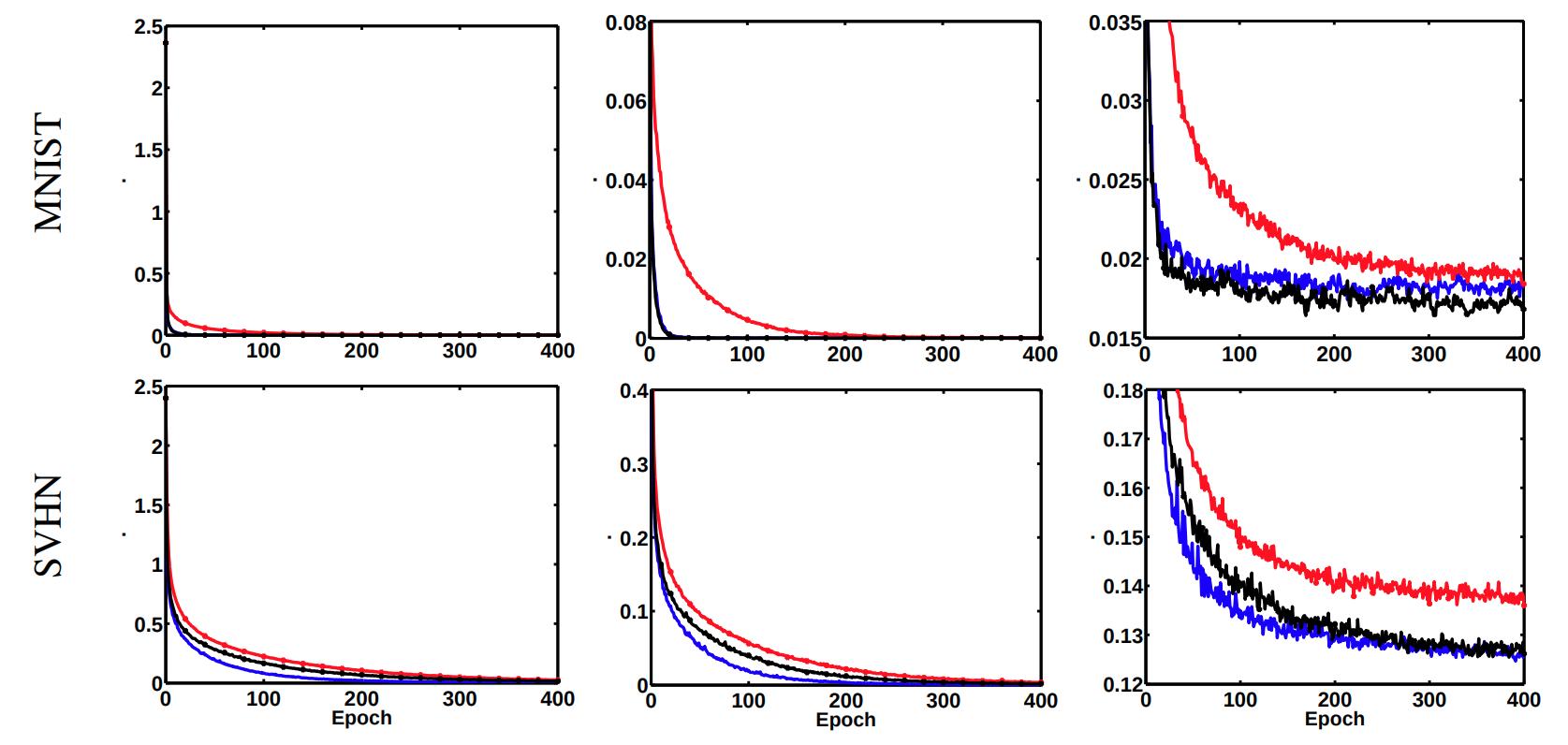
They train a multilayer perceptron with two hidden layers of 4000 neurons each. With mini batches of size 100 and learning rate \(10^\alpha\) where \(\alpha\) is an integer between 0 and 10, chosen for each dataset with respect to the smallest validation error. They trained the networks with and without dropout.
They tried balanced and unbalanced networks. For the balanced nets they initialize with Gaussian distribution. For unbalanced nets, they choose 2000 hidden neurons and perform a rescaling with factor \(10c\) where c was chosen randomly for each neuron from a log-normal distribution.
The curves generated by Path-SGD for balanced and unbalanced networks are identical, so they only plot one.
For the experiments with dropout they suppressed the results on unbalanced nets due to very poor results.

Conclusion

Path-SGD exploits the fact that the geometry of the weight space for ReLU networks is not Euclidian due to positive homogeneity
Path-SGD seems to perform better than SGD and AdaGrad across different datasets
However, more recent work shows that Path-SGD is not computationally efficient on very deep networks.