(Image taken from HERE)

Highlights

InfoGAN is a GAN that can learn a disentangled latent space distribution in an unsupervised manner.

Introduction

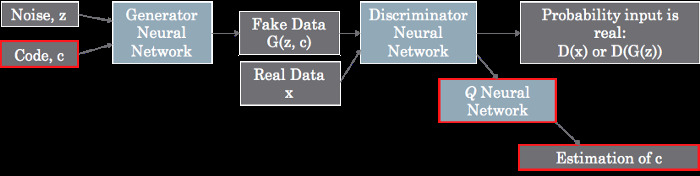
A basic GAN is illustrated with the graph in the previous figure but without the red boxes. The main idea of InfoGAN is to add two little things to the basic GAN (the red boxes!).

First and foremost, InfoGAN use an extra latent vector (called code): \(c=(c_0, c_1, ..., c_n)\) that is appended to the original latent input vector \(z\). Doing this turns the original generator \(G(z)\) into \(G(z,c)\).
In order to make sure the generator does not simply ignore \(c\), InfoGAN adds to the loss function a mutual information term. In this way, the loss goes from a normal GAN loss

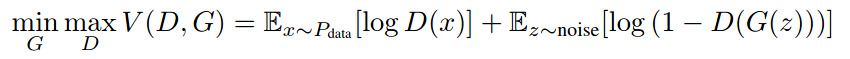
to an infoGAN loss

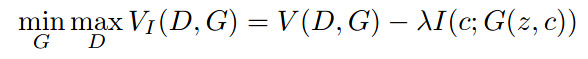
The point of the mutual information term is to make sure that the produced image depends on the input vector \(c\). The minus sign in front of \(\lambda\) is there because \(G\) aims at minimizing the loss and that \(I\) is strictly positive and maximal when the generated images are totally dependent of \(c\).

Considering that the mutual information equation is given by

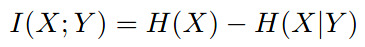
where \(H\) is the entropy, the authors argue that this value is hard to compute because it depends on the posterior $$P(c

x)\(which is a priori unknown. As a workaround, they use a proxy\)Q(c’

x)$$, thanks to the variational inference theory.

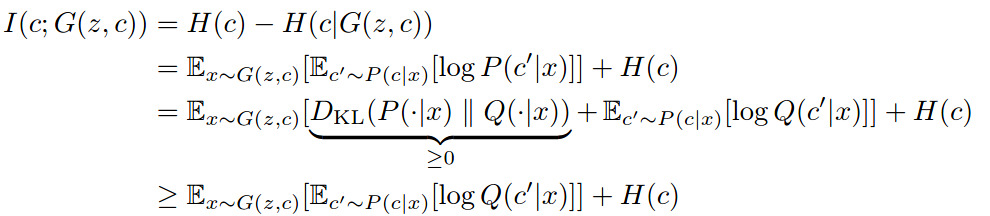
This brings us to the second GAN improvement: by the very nature of deep neural nets, $$Q(c’

x)$$ is approximated by a neural network appended to the discriminator network (c.f. top figure). The resulting loss becomes :

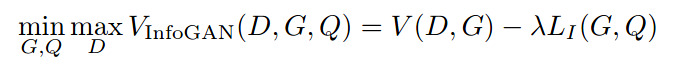
where \(L_I\) is \(Q\)’s loss (crossentropy or other).

Results

Results are quite convincing with well disentangled distributions.