Highlights

  • Unsupervised “skill” discovery without extrinsic rewards
  • Planning in “skill” space allows to generalize to unseen tasks

Introduction

Model-based reinforcement learning (MBRL) tries to learn the dynamics of the environment as well as a policy that plans the optimal course of action using the learned dynamics. This allows the policy to be learned in more sample-efficient way as well as making able to generalize to new tasks.

However, generalizing to new state distributions remains an open problem, as exploring the full state-space and learning the full dynamics for high-dimensional systems is generally infeasible. The authors want to retain the flexibility of MBRL by using the simplicity of model-free RL to learn low-level behaviors that can be leveraged at test time.

Methods

The authors want to learn the dynamics for a large and diverse set of skills, which allows them to use model-based planning in the skill space (or behavior space, the terms are used interchangeably) for solving new tasks.

Unsupervised skill discovery

Using the common MDP \(M = (S, A, p, r)\), they want to learn a skill-conditioned policy \(\pi(a \vert s,z)\) with \(z \in \mathbb(Z)\) that can be sampled from a prior \(p(z)\). To plan in the skill space, the authors also propose to learn the dynamics for skills \(q_{\theta}(s'{\vert}s,z)\), which will be used to plan at test time. The authors argue that learning the dynamics of the environment only for certain skills is much easier than learning the whole environment dynamics (aka for all possible behaviors).

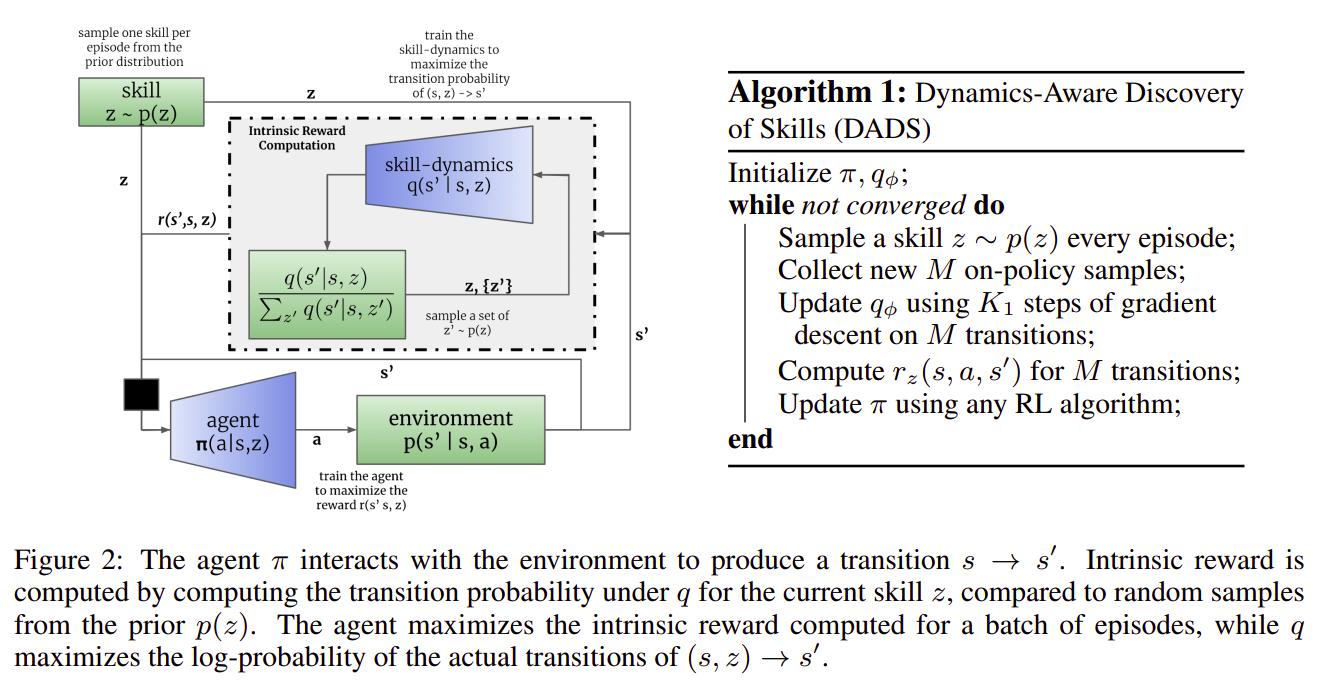
To discover skills, the authors propose to maximise the mutual information (MI) between the next state \(s'\) and the skill \(z\) conditioned on the current state \(s\) s.t.

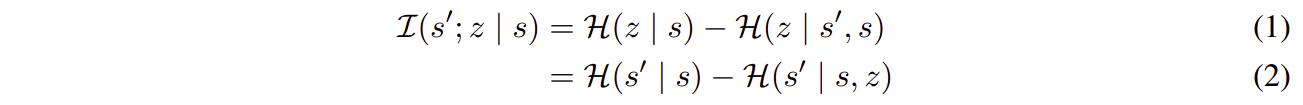
Maximizing eq.2 means promoting the diversity of transitions from \(s\) to \(s'\) (therefore maximizing the probability of learning relevant skills), while making the transitions for a given \(z\) predictable (thus making the process stable).

Because the actual dynamics are unknown but can be sampled, maximizing (2) is intractable, but the objective can at least be lower-bounded by

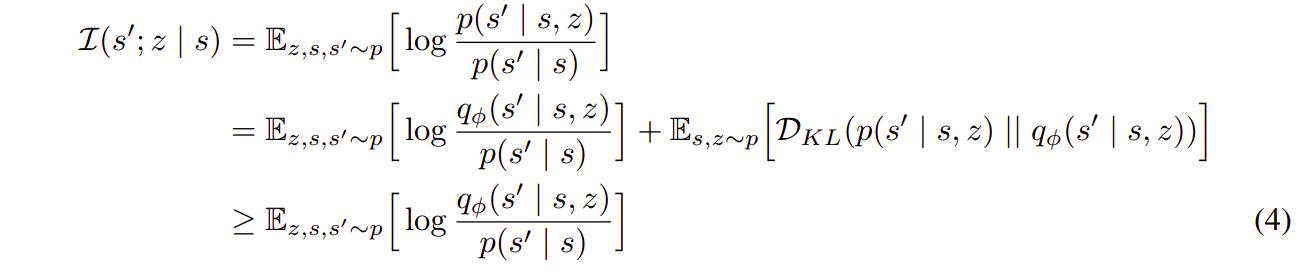
Which leads to the following gradient update for \(q_{\theta}\)

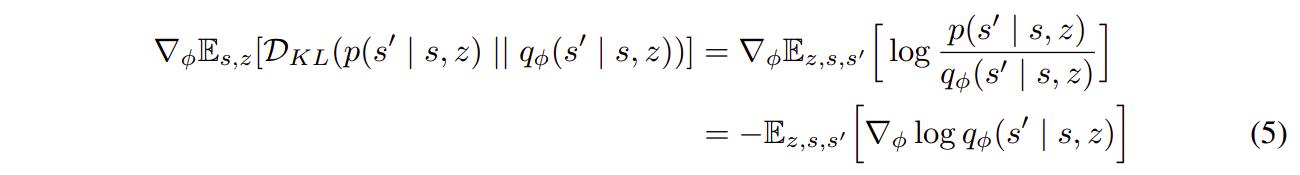
which corresponds to maximizing the likelihood of samples from \(p\) under \(q_{\theta}\).

To make use of the learned dynamics, the authors propose to train a policy using any model-free RL algorithm using the following instrinsic reward function

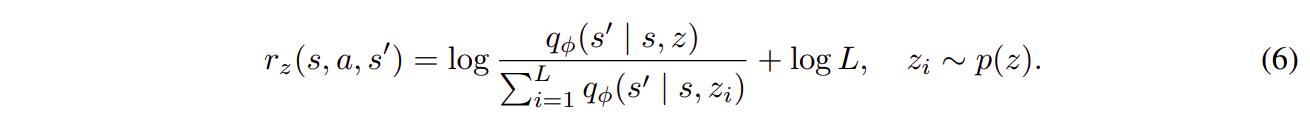
with \(L\) the number of samples drawn from \(p(z)\). Again, the reward function encourages the policy to produce transitions that are predictable under \(q_\theta\) as well as diversified.

In implementation, the authors use the Soft Actor-Critic algorithm to train their policy, and their prior \(p(z) = U(-1, 1)^D\) where \(D\) is the dimentionality of the input space.

Planning in action space

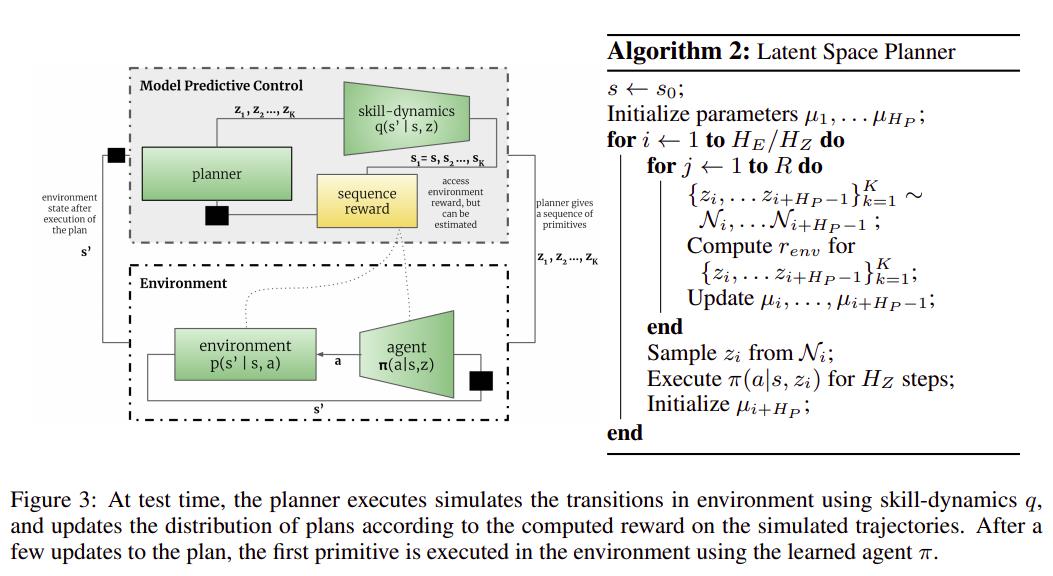
To make use of the low-level behaviors learned, the authors suggest planning in behavior space, instead of state-space as is usually done with MBRL. To do so, the latent space \(p(z)\) is sampled according to the \(\mu\)s in fig. 3 and a few short trajectories are sampled using the learned prior-dependant dynamics. Presuming access to the reward function, the reward is computed for the candidate trajectories and the best one is selected. A few steps from the selected plan are executed in the environment, the \(\mu\)s are recomputed to promote behaviors corresponding to the reward function as

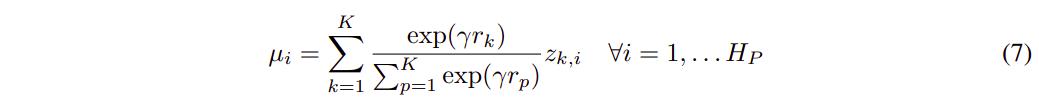
and the whole planning process is repeated.

Results

Qualitative

DADS can discover primitives for Half-Cheetah to run forward and backward with multiple different gaits, for Ant to navigate the environment using diverse locomotion primitives and for Humanoid to walk using stable locomotion primitives with diverse gaits and direction. Qualitatively, we find the skills discovered by DADS to be predictable and stable, in line with implicit constraints of the proposed objective. While the Half-Cheetah will learn to run in both backward and forward directions, DADS will disincentivize skills which make Half-Cheetah flip owing to the reduced predictability on landing. Similarly, skills discovered for Ant rarely flip over, and tend to provide stable navigation primitives in the environment. This also incentivizes the Humanoid, which is characteristically prone to collapsing and extremely unstable by design, to discover gaits which are stable for sustainable locomotion.

Against MBRL

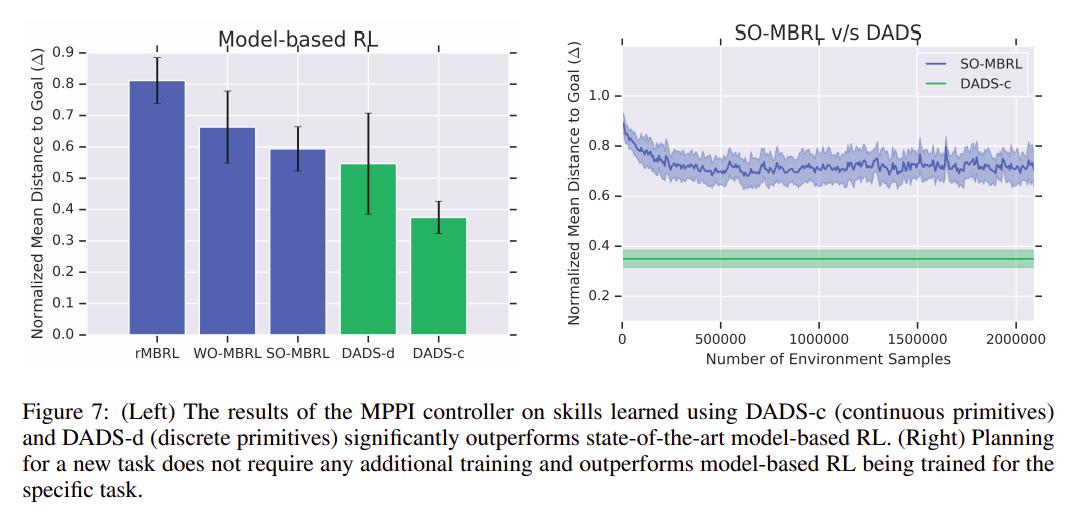
DADS can achieve better performance than state-of-the-art MBRL with variying degrees of directed exploration on having the Ant Mujoco model travel to a random point.

Against hierarchical RL and model-free RL

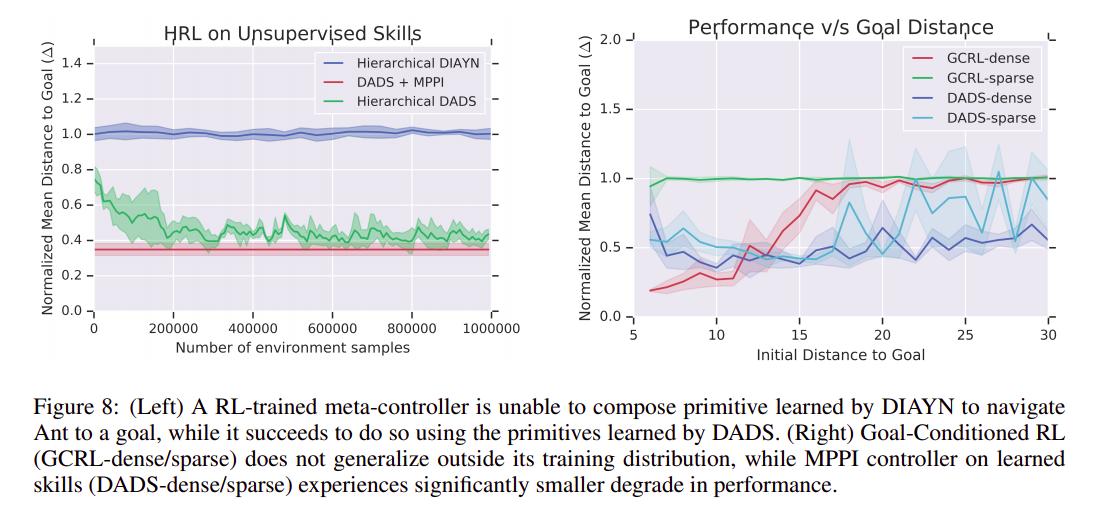
Same goal as against MBRL.

Conclusions

We have proposed a novel unsupervised skill learning algorithm that is amenable to model-based planning for hierarchical control on downstream tasks. We show that our skill learning method can scale to high-dimensional state-spaces, while discovering a diverse set of low-variance skills. In addition, we demonstrated that, without any training on the specified task, we can compose the learned skills to outperform competitive model-based baselines that were trained with the knowledge of the test tasks.

Remarks

  • It took me a while to figure out how planning was done until I went on the Openreview page and read that the model has access to the reward function

References