Highlights

  • Authors propose a machine-learning (ML) method to estimate the number and orientations of fascicles in a voxel.
  • Their method predicts the number and orientations of crossing fascicles more accurately than several existing standard methods.

Introduction

Existing methods for estimating the number and orientations of fascicles in an imaging voxel either depend on non-convex optimization techniques that are sensitive to initialization and measurement noise, or are prone to predicting spurious fascicles. Authors propose a machine-learning method to overcome such shortcomings. For each direction in the unit sphere all DW-MRI measurements in the voxel are used to estimate the angle to the closest fascicle for that direction. This information is then used to estimate the number and orientations of major fascicles or used directly for tractography.

Methods

To estimate the angle to the closest fascicle for a given direction in the unit sphere, they use a feature vector representing a weighted average of the diffusion measurements as a function of the angular distance to the considered directions in the unit sphere containing contributions from:

  • The diffusion signal.
  • The angular orientation gap between the considered orientation in the unit sphere and the gradient encoding vector.
  • A weighting factor to account for the closeness of the gradient encoding vector to the cone.

For each direction in the unit sphere, the feature vector is a \(15\)-dimensional vector representing a cone around the considered direction. A Multi-Layer Perceptron (MLP) receiving the feature vector is used for estimation purposes. The resulting angular predictions are smoothed, processed and thresholded in order to obtain the underlying fiber population orientations.

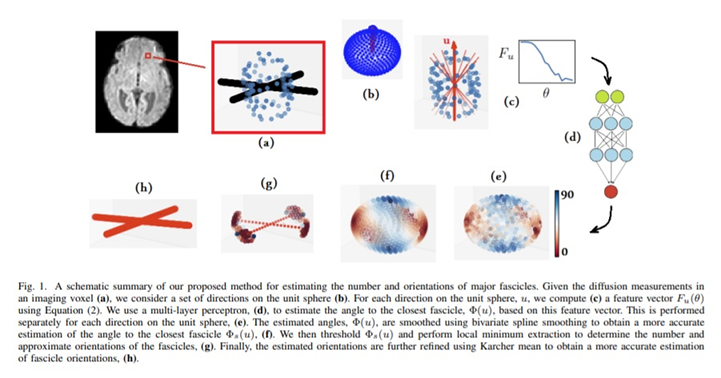
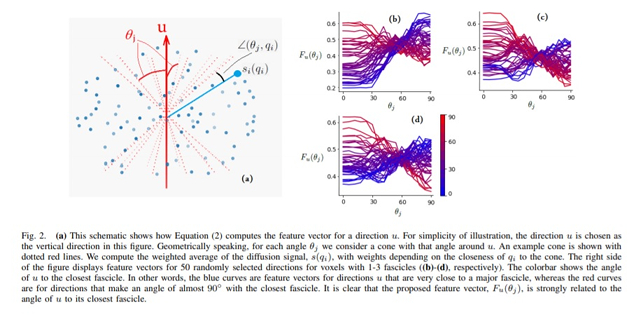
Contrary to other local reconstruction methods that optimize for all unit sphere directions at the same time, the present method performs an estimation on every direction separately and does so using all available diffusion data.

They compared their method to:

  • Automatic Relevance Determination (ARD)
  • Multi-tensor model fitting (using two different variants)
  • Constrained Spherical Deconvolution (CSD)
  • Sparse Fascicle Model (SFM)

The reported measures were:

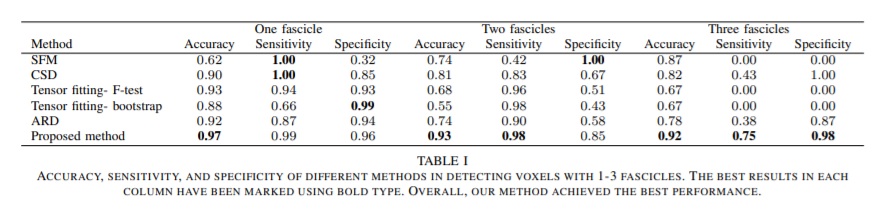
  • The accuracy, sensitivity and specificity for the number of fascicles estimation error.
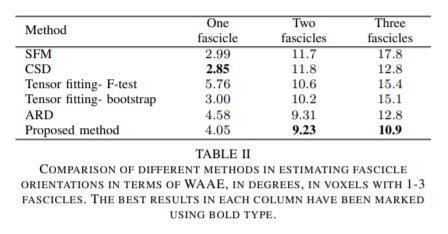
  • The Weighted Average Angular Error (WAEE) for the fascicle orientation estimation error quantification. The measure imposes an unequal weight depending on the fascicle occupancy penalizing more severely error on larger fascicles.

Data

They tested their method both on simulated and real diffusion data. The simulated testing data used was the 2013 HARDI Reconstruction Challenge Phantom. Since the model and diffusivity values for the phantom were not known, authors trained on a multi-tensor model for different axial and radial diffusivity values with up to three fiber voxels. As the real diffusion data, they used the developing Human Connectome Project (dHCP) dataset. The ground truth for the for the real dataset was generated using CSD using all available shell data. Then training and testing was done on the \(b=1000 s/mm^2\) shell data.

Results

The presented outperforms the standard methods in multi-fiber population voxels. Although standard methods are better at predicting the orientation at single fiber population voxels, the difference in performance is small and their method obtains high scores consistently across all measures.

Quantitative evaluation on the 2013 HARDI Reconstruction Challenge Phantom dataset:

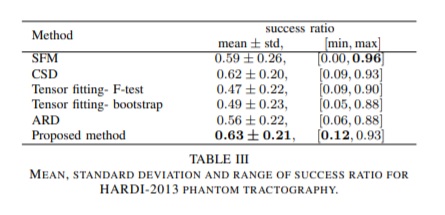
Qualitative comparisons of the methods were carried out on the real dataset. The assessment was done by an expert neuroanatomist on the tractograms derived using the local reconstructions provided by each method.

Authors additionally computed the robustness of their method when using a down-sampled version of the real dataset diffusion measurements. Their method compared better to CSD in terms of the mean angular error of the major fiber population orientation.

Conclusions

The presented method offers a higher accuracy than several competing methods in detecting voxels with two or three fascicles, as well as estimating fiber orientations.

Comments

  • RUMBA was not included when assessing the performance of the method on the 2013 HARDI Reconstruction Challenge Phantom. RUMBA was ranked first for HARDI-like acquisition data (which is the one used in this paper) in that challenge.
  • As mentioned in the paper, other methods based on deep-learning methods have been proposed in recent years to estimate fODFs. The benefits of their method compared to the former are unclear. Similarly, no quantitative comparison against these methods is presented.