Introduction

In this paper, the authors focus on the following open question:

Why does minimizing the empirical error during deep neural network training leads to good generalization?

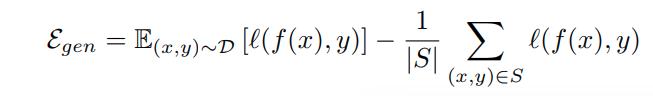
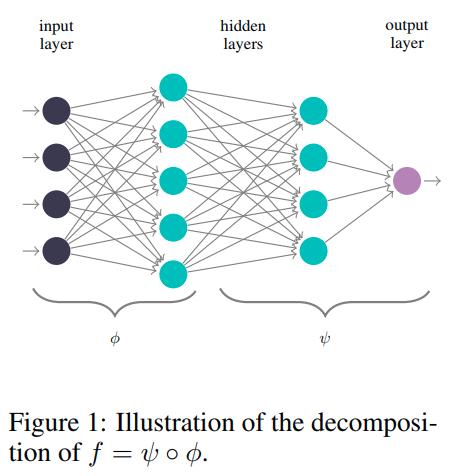
They propose to look at feature robustness of the network function, which measures the robustness of a function \(f= \psi \circ \phi : X \to Y\), where the function \(\phi : X \to \mathbb{R}^m\) is considered as a feature extraction that maps an input to the feature space \(\mathbb{R}^m\), and the map \(\phi\) is a classifier.

A function \(f\) is \(\epsilon\)-feature robust on a dataset \(S\) if small changes in the feature space defined by \(\phi\) do not change the empirical error by more than \(\epsilon\).

Feature Robustness

Feature robustness is supposed to measure the mean change in loss over a dataset under small changes of features in the feature space.

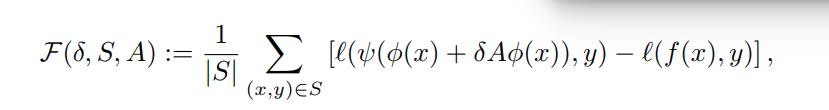
Observe that the feature space \(\mathbb{R}^m\) can be perturbed by a matrix \(A \in \mathbb{R}^{m \times m}\).

Measures of Flatness

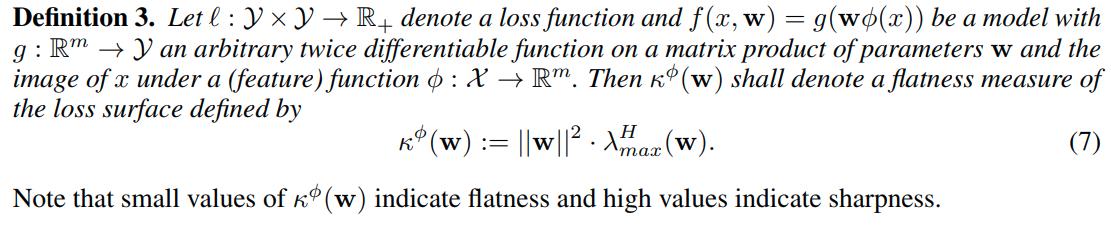
We can also consider the hidden layers of a neural network as feature spaces.

Let \(**w^l**\) denote the weight matrix of the l-th hidden layer of a neural network.

Empirical work suggests that the trace of the Hessian is a good average of the spectrum. With respect to the trace of the Hessian, they prove the following:

It becomes natural to define:

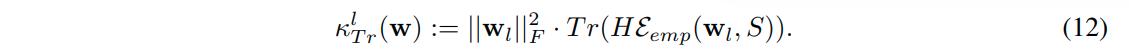
Feature Robustness and Generalization

The generalization error can be rewritten as:

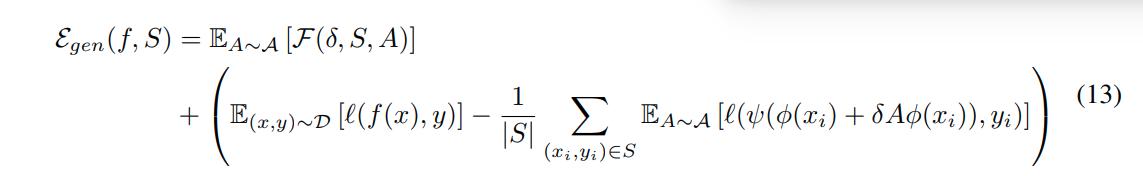
In order to bound the generalization error, the authors define the following:

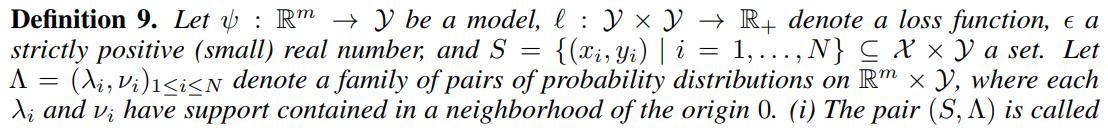
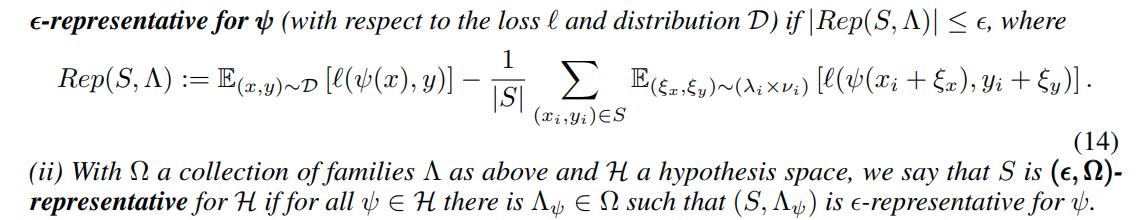
The main theorem then is:

Experiments

For measuring the generalization error, they employ a Monte Carlo approximation of the target distribution defined by the testing dataset and measure the difference between loss value on this approximation and empirical error.

They compute the generalization error as the difference between summed error values on test samples multiplied by 5 and summed error values on the training set since the size of the training set is 5 times larger. Also, the Hessian is computed on the training set.

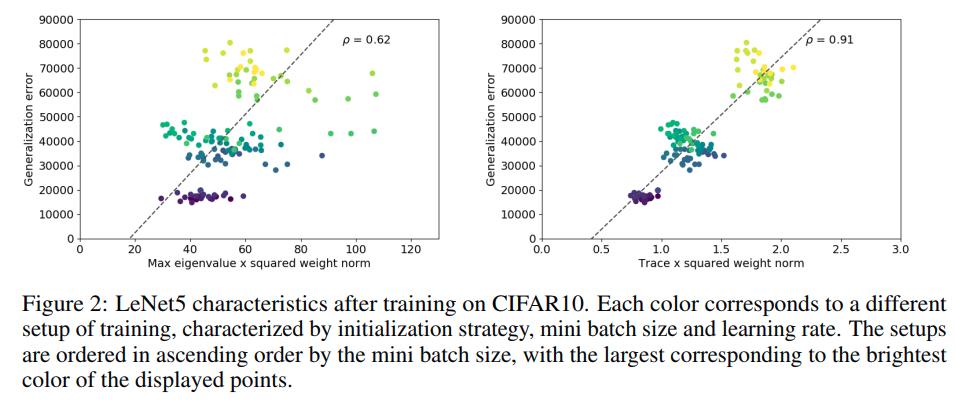
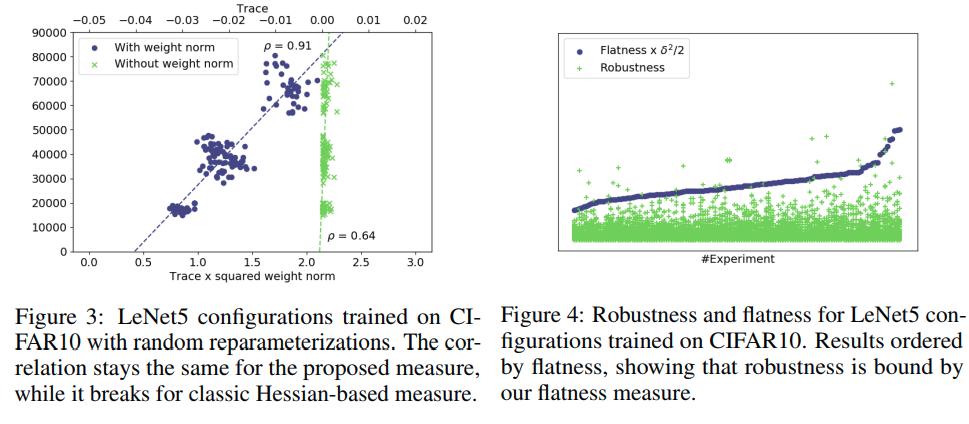
Conclusion

In this paper, the authors provide a new measure of flatness by using mathematical results concerning feature robustness.

These measures are invariant under reparametrization of ReLU neural networks.
These measures are empirically correlated to generalization.