Introduction

Generalization of neural networks has been linked to the flatness of the loss landscape around the found minimum. Therefore, it is reasonable to look for measures of flatness so that we can impose those measures into the learning so that we can ensure we get a minimum that generalizes better.

In this paper the authors prove that three notions of flatness for minima of deep networks do not actually measure flatness. They do this by using positive scale invariance of ReLU networks.

• This is a machine learning paper without experiments and only math.

Notions of flatness to be debunked

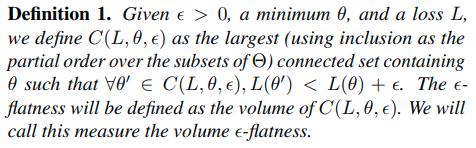
• There is also a notion of flatness concerning the Hessian, namely the spectral norm and trace of the Hessian. These two have information from the eigenvectors of the Hessian.

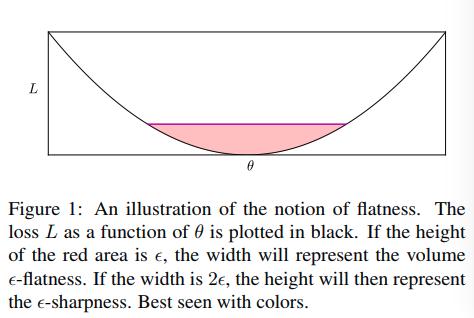
Properties of ReLU

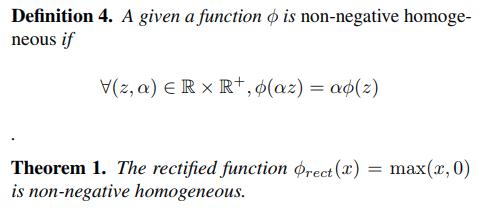
• The maps \(T_\alpha\) produce networks with the same network function.

Theorems

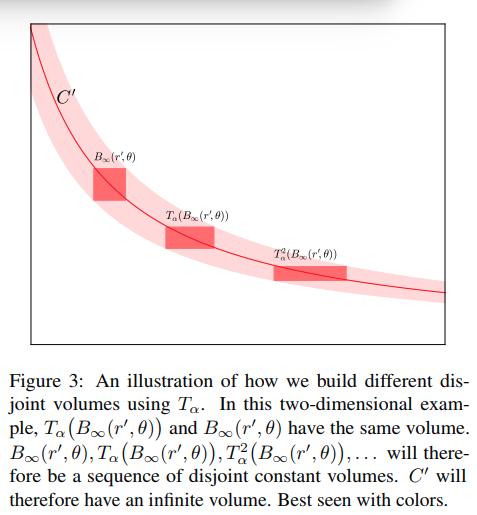
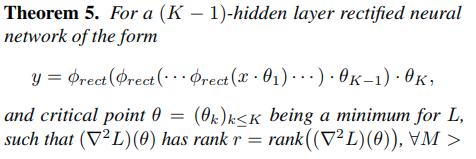
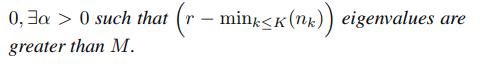
What they prove now is that the notion

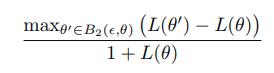
for sharpness can also be modified with the maps \(T_\alpha\).

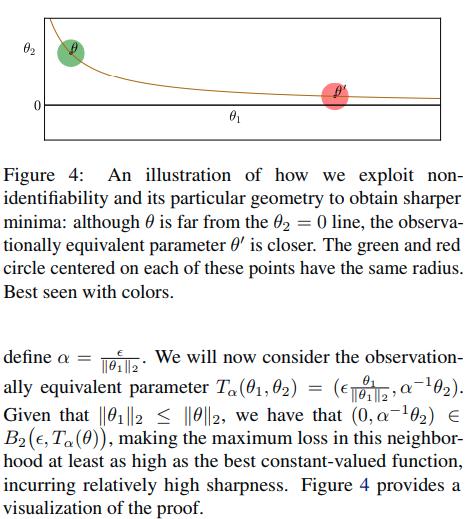
Reparametrization

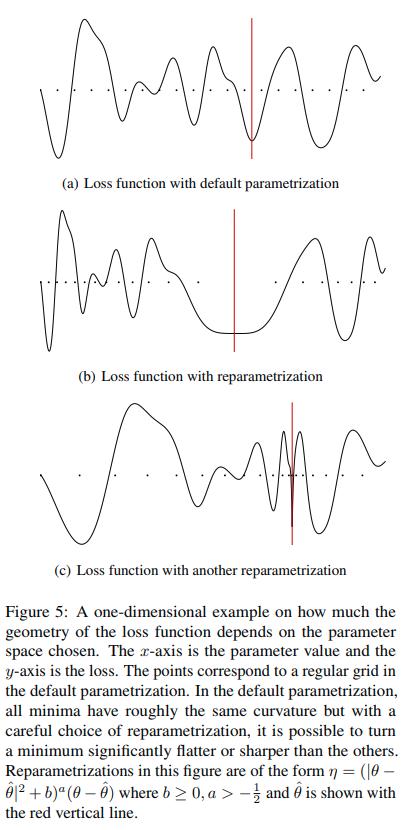
Conclusion

• Previously used definitions of flatness fail to account for the complex geometry of some commonly used deep architectures.
• Positive scale invariance allows one to alter the flatness of a minimum without affecting the network function.
• A measure of flatness of a minimum of a ReLU network has to take into account its positive scale invariance.