Introduction

In this paper, they show that when using batch normalization and weight decay one can use an exponentially increasing learning rate and still have good results. They also present a mathematical proof that the exponential learning rate is equivalent to BN + SGD + StandardRateTuning + WeightDecay + Momentum.

• It is usual when using BN to lower the learning rate when the validation loss is plateau-ing.

They use scale invariance to manage the computations on the proofs, namely:

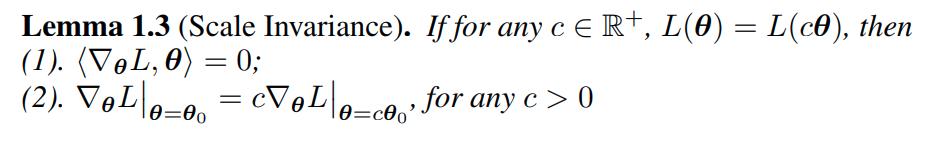
Warm-up

First, they show that Fixed LR + Fixed WD can be translated to an equivalent Exponential LR. Consider the following notation

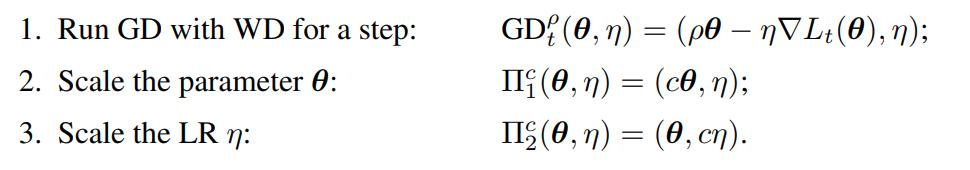
Then the theorem reads:

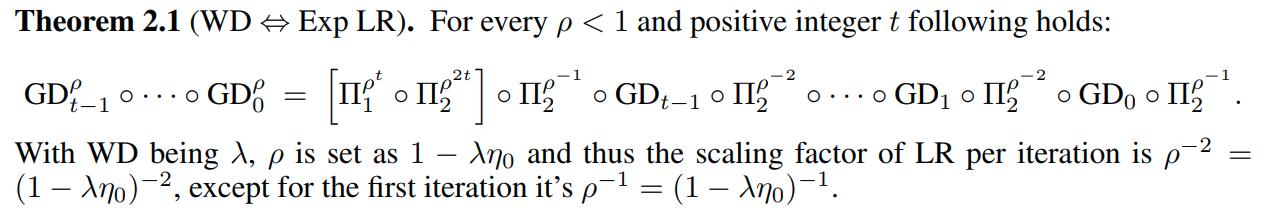
Main Theorem

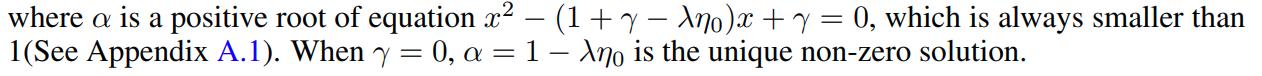
An example of this theorem is:

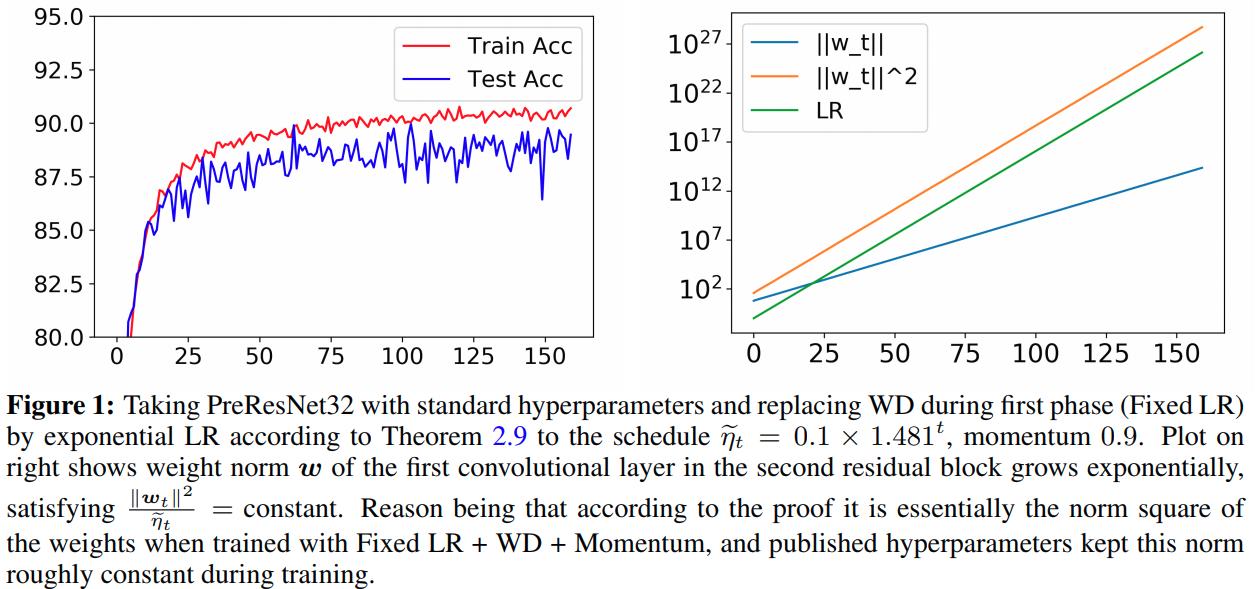
Correcting Momentum

A definition of Step Decay is needed to understand the useful exponential learning rate schedule

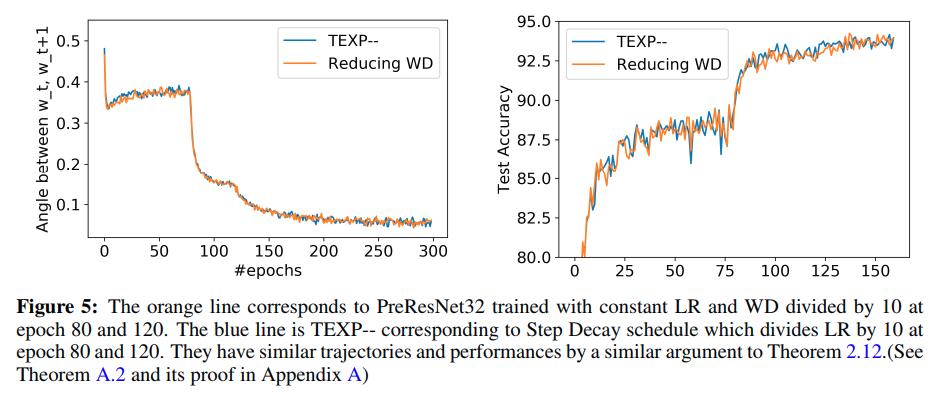
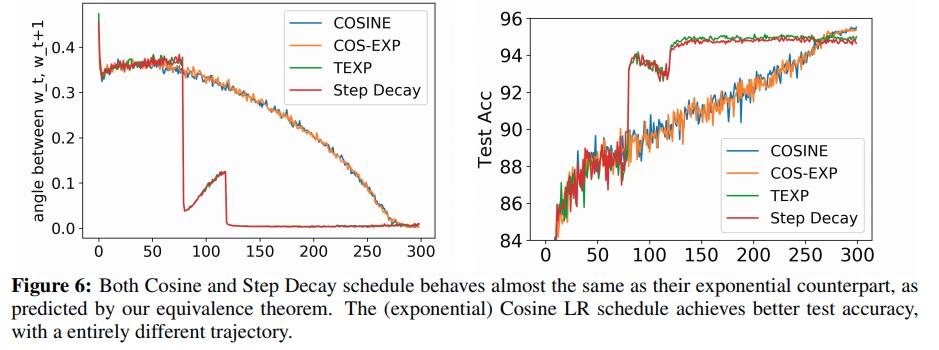
Testing the mathematical equivalence they get:

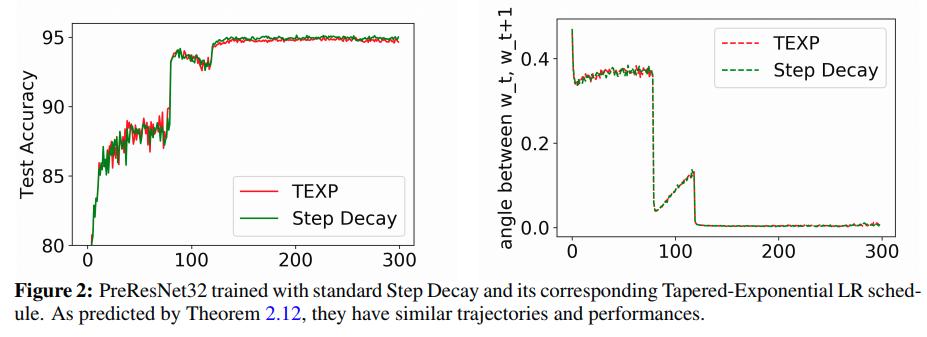
More Experiments

The TEXP learning rate contains two parts when entering a new phase (i.e. training period where the learning rate changes and then stays the same for a while):

• An instant learning decay \(\frac{\eta_I}{\eta_{I-1}}\).
• An adjustment of the growth factor \(\alpha_{I-1}^* \to \alpha_I^*\).

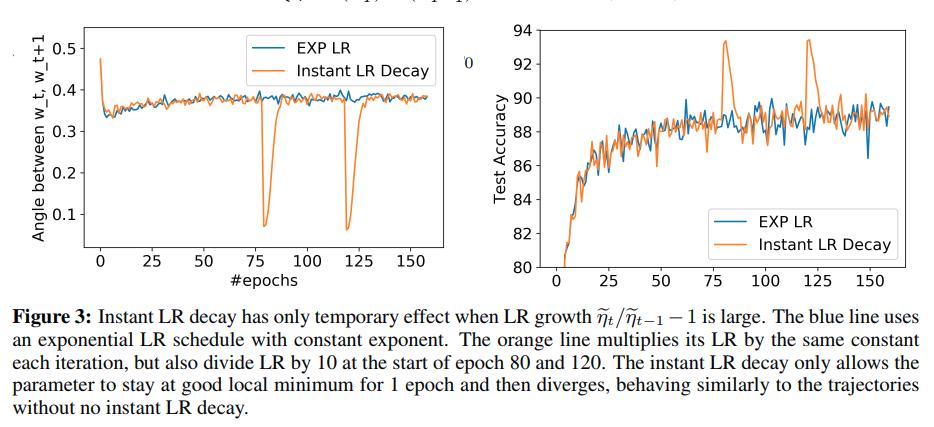
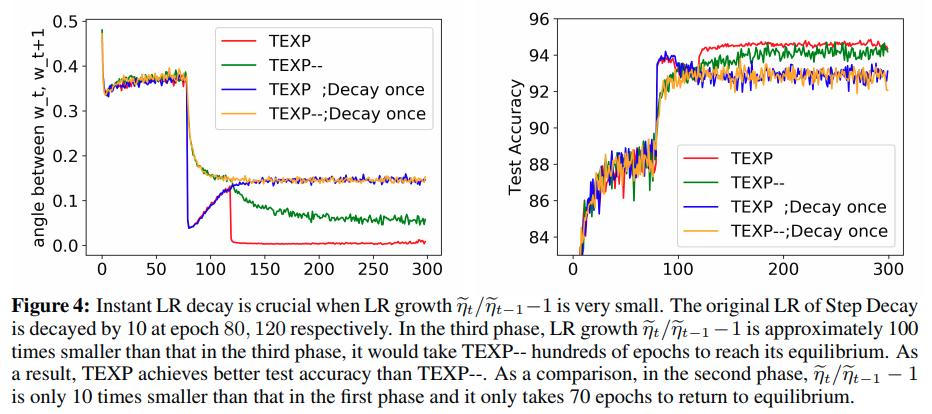
Conclusion

• This shows that Batch Normalization allows very exotic learning rate schedules, and verifies these effects in experiments.

• The learning rate increases exponentially in almost every iteration during training

• The exponential increase derives from the use of weight decay, but the precise expression involves momentum as well

So the authors conclude that: the efficacy of this rule may be hard to explain with canonical frameworks in optimization.