In this work, the author tackles the notion that L2 regularization and Batch Normalization (or other normalization methods) have non-trivial interactions.

In short:

BN makes the function (layer) invariant to the scale of the weights; thus, L2 loses its regularizing influence on model performance
BN makes the gradients decay as the scale of weights increase; thus, if the weights are unbounded, the gradients converge towards zero
In layers with BN, L2 regularizes the gradients by regularizing the scale of the weights

Note that the above points also apply for Weight Norm and Instance Norm.

Theory

In the following, \(y\) represents the output of a layer, i.e. a sequence of (FC, Normalization, Nonlinearity). Below, \(y_{\textrm{BN}}\) is the output when Batch Norm is used:

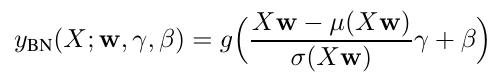
Let’s introduce the shortcut \(L_\lambda\):

Invariance to the scale of weights

By replacing \(\mathbf{w}\) with \(\alpha\mathbf{w}\) in the formula above, we get, using the properties of the mean and standard deviation, that \(\alpha\) cancels out:

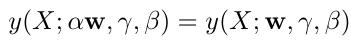
Thus, we get that:

\[L_{\lambda}(\alpha\mathbf{w}) = \sum_{i=1}^{N} \ell_{i}(y(X_i;\mathbf{w},\gamma,\beta)) + \lambda ||\alpha\mathbf{w}||_2^2 = L_{\lambda\alpha^2}(\mathbf{w})\]

which means that scaling the weights by \(\alpha\) is equivalent to not scaling them, if the regularization weight \(\lambda\) is scaled by \(\alpha^2\). According to the author, the parameter \(\lambda\) has no impact on the optimum, since the weights can be scaled to compensate.

Impact on the gradients, and the effective learning rate

Let’s write down the gradient of \(y\):

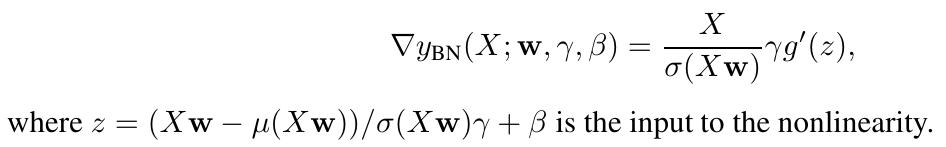
Then, let’s see the impact of a scaling on the value of the gradient of the loss:

The author concludes: L2 regularization is still beneficial when training neural networks with Batch Normalization, since if no regularization is used the weights can grow unbounded, and the effective learning rate goes to 0.

For a definition of the effective learning rate, please refer to the paper.

Direct weight normalization update

To decouple the scale of the gradients from \(\lambda\), we can force the weights to have a constant scale:

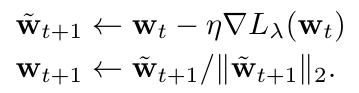
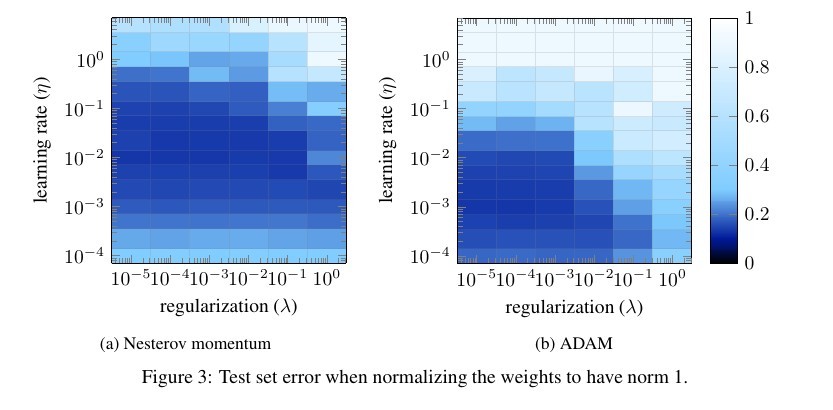
We will see below that, in typical training regimes, using this update makes \(\lambda\) no longer affect the test error.

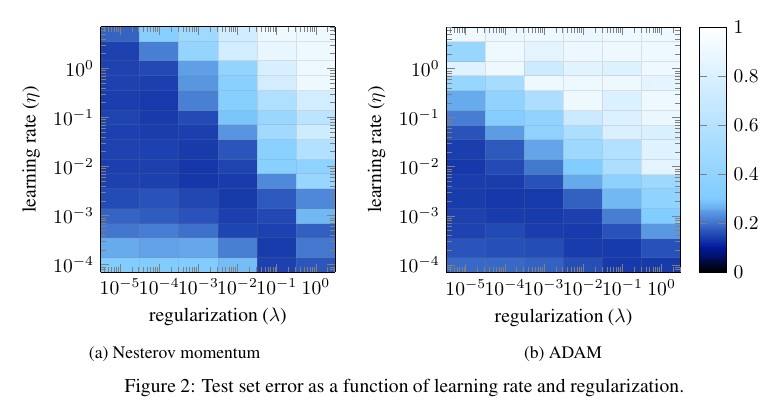
Experiments

The dataset used is CIFAR-10, and the model is a simple 4-layer ConvNet. More details in the paper.

For ADAM, the effective learning rate is \(\sqrt[3]{\eta^2 / \lambda}\). On the right below, on diagonals where the effective learning rate is constant, the test error is roughly constant:

For values of \(\lambda\) that are not too large (so that the gradients coming from L2 are not overwhelming), \(\lambda\) has pretty much no effect on the test error:

Blog post

The following blog post is a very noice complement to the paper: https://blog.janestreet.com/l2-regularization-and-batch-norm. It brings more experimental insights, and interesting plots.