Highlights

Novel hierarchical probabilistic method for modelling the conditional distribution of segmentation masks given an input image
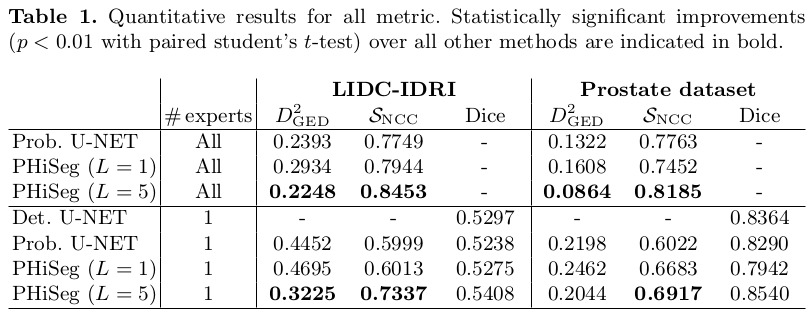
Method outperforms the state-of-the-art on a number of metrics
PHiSeg was able to predict its own errors significantly better compared to previous work

Introduction

Medical segmentation problems are often characterized by ambiguities due to inherent uncertainties such as:

Restrictions imposed by the image acquisition (e.g. poor contrast)
Variations in annotation “styles” between different experts

To account for uncertainty, different methods have already been proposed, but they all have downsides:

Bayesian networks: samples may vary pixel by pixel and miss complex correlation structures
Ensemble networks: fixed number of hypotheses
Probabilistic U-Net: samples with limited diversity

The proposed method is inspired by Laplacian Pyramids, generating segmentation samples at low-resolution and continuously refining the distribution of segmentations at increasingly higher resolutions. An example of the gradual outputs is shown in figure 1.

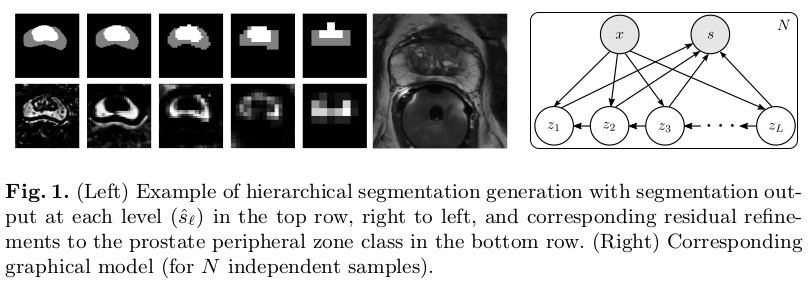
Methods

The overall proposed end-to-end architecure is detailed in Figure 2. Note that the posterior and prior networks have identical structure but do not share any weights.

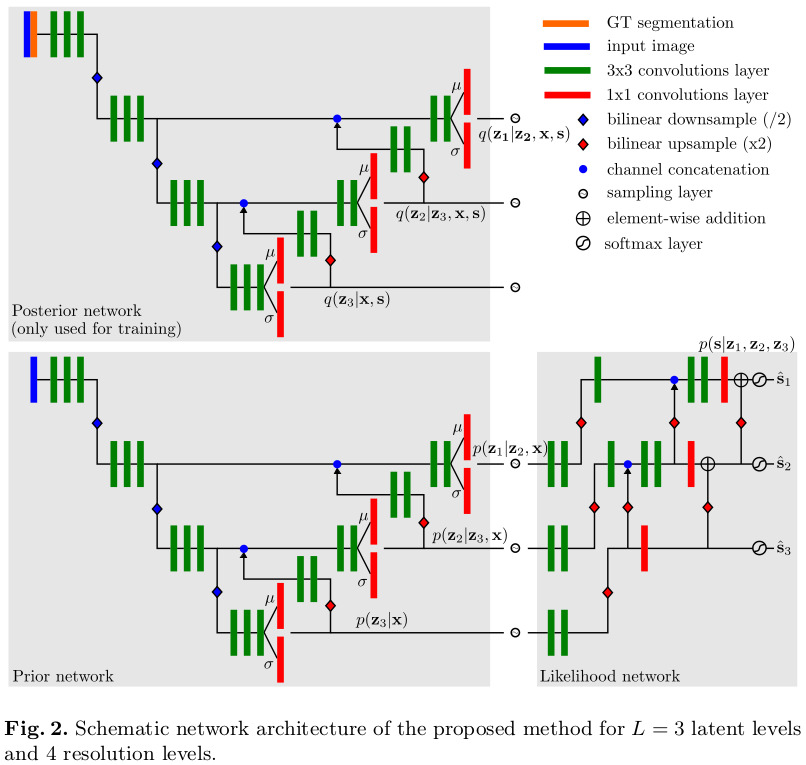
According to the authors, it is important that the likelihood network only applies residual changes, since it forces all levels to learn a part of the representation. Otherwise, the higher resolution levels could learn to simply the input they receive from earlier levels.

The methods’ main loss is detailed in equation 2:

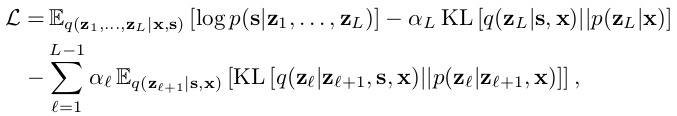
The prior and posterior distributions are parameterized as axis aligned normal distributions \(N(z|\mu, \sigma)\), like detailed in equations 3 and 4:

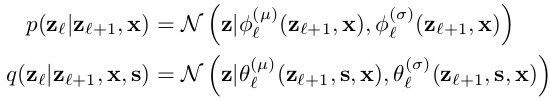
To ensure stable training, the authors mentions that they need to deviate from their theory in 2 cases:

The magnitude of the KL terms depends on the dimensionality of \(z\). However, since the dimensionality of \(z\) grows with \(O(2^l)\), this led to optimization problems. To counteract this, the authors heuristically set the weights \(\alpha = 2^{l-1}\) in Eq. 2.
To enforce the desired behavior that \(z_l\) should only model the data at its corresponding resolution, a reconstruction loss was added to the upsampled output of each level: \(CE(ups(\hat{s}_{l}), s_{gt})\) for \(l \gt 1\)

Data

The method was tested on two datasets:

Publicly available LIDC-IDRI which comprises 1018 thoracic CT images with lesions annotated by 4 radiologists
In-house prostate MR dataset of 68 patients acquired with a transverse T2-weighted sequence. The transition and peripheral zones were manually annotated by 4 radiologists and 2 non-radiologists.

In both cases, the authors took centered crops of the regions of interest to feed to the method.

Two experiments were designed to evaluate the method.

Assess how closely the distribution of generated samples matched the distribution of ground-truth annotations by training the methods using the masks from all available annotators
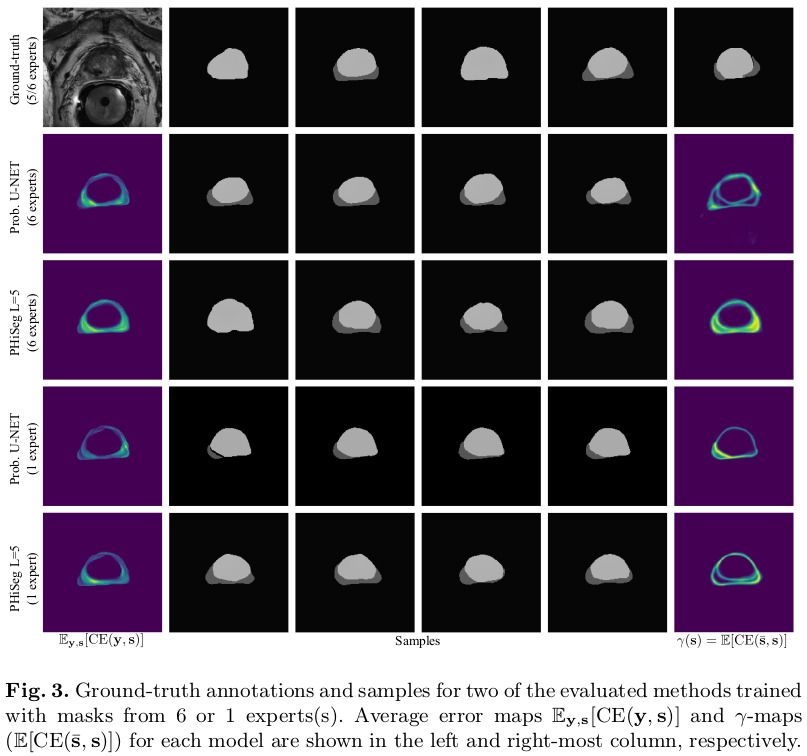
Investigate the models’ ability to infer the inherent uncertainties (train using only one of the annotations, and test on all available annotations)

Results

Remarks

In the paper, there seems to inconsistencies about which distributions (prior, posterior) are conditioned on which data (\(x\), \(z\), \(s\)). The conditioning that makes the most sense to me is the one from Figure 2 and equations 3 and 4.