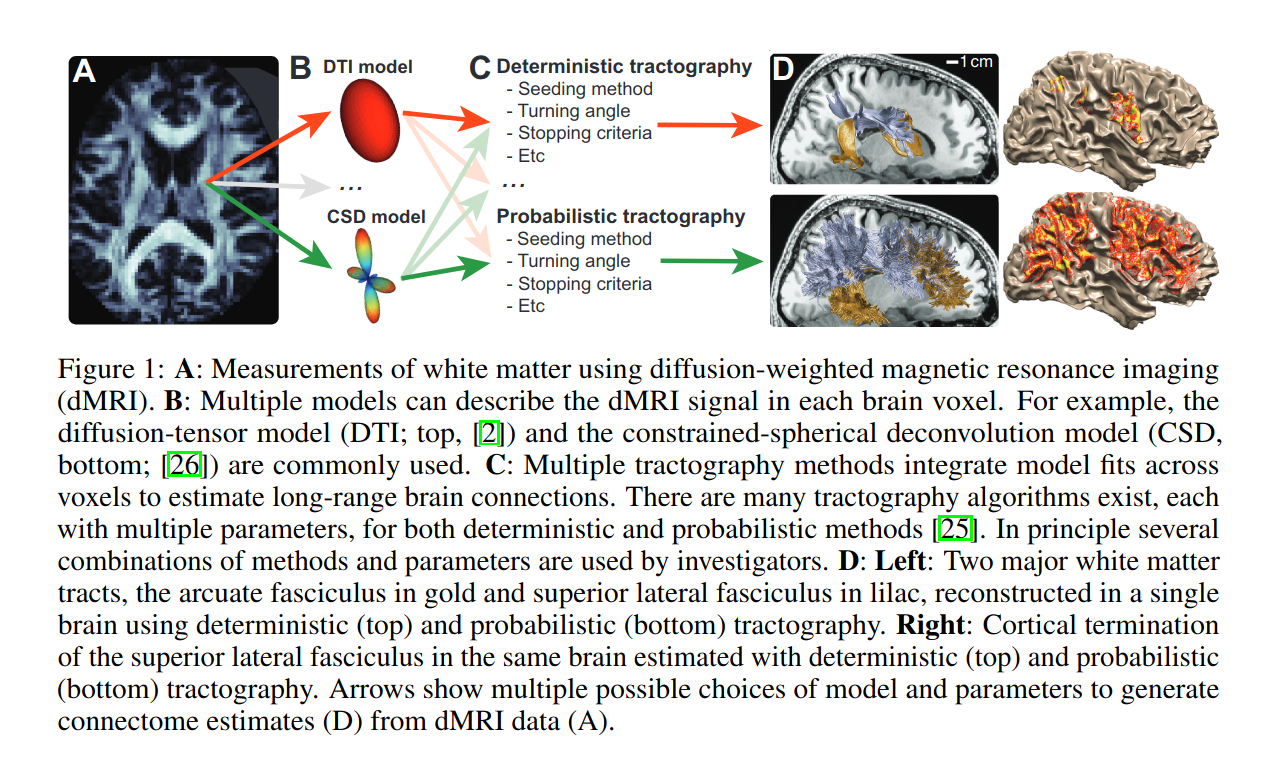
Learning Macroscopic Brain Connectomes via Group-Sparse Factorization
Code: [https://github.com/framinmansour/Learning-Macroscopic-Brain-Connectomes-via-Group-Sparse-Factorization] Video: [https://www.youtube.com/watch?v=DLnWhExtopw]
Highlights
- Replace rule-based/expert-based choice of tractography models and parameters
- Unsupervised model for generating a tractogram using a sparse factorization
Method
Factorization of a tractogram/connectome
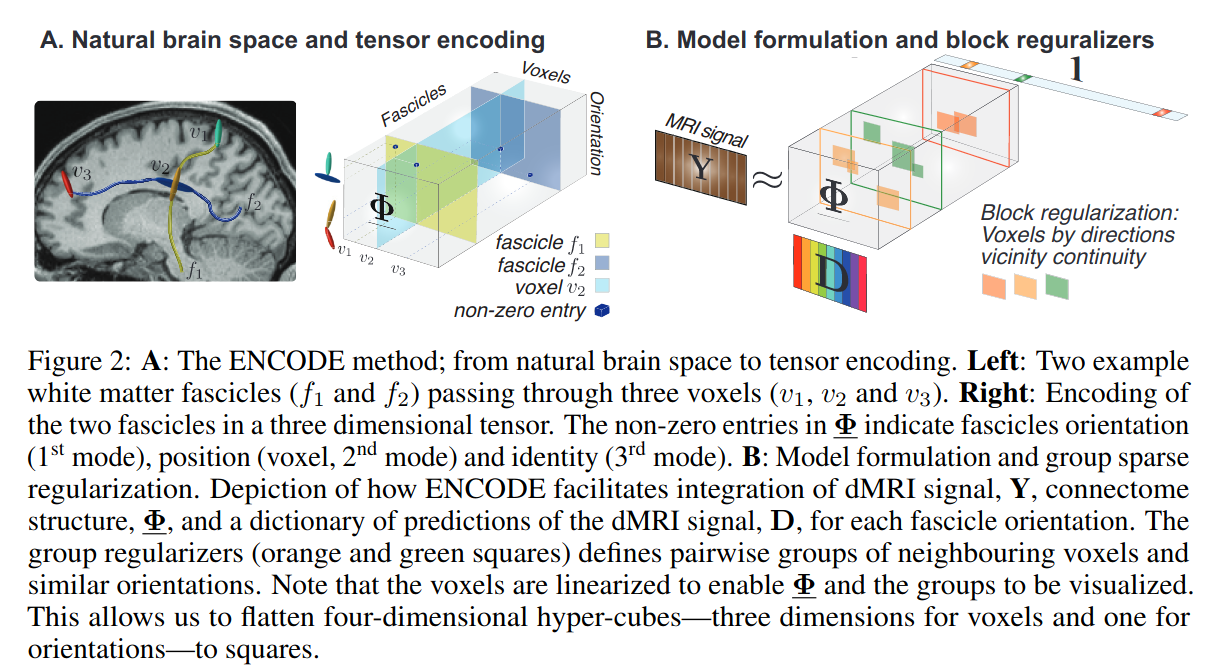
A tractogram is represented by a 3D sparse matrix \(\Phi\), where:
- 1st dimension is the flattened, discretized orientations over the hemisphere
- 2nd dimension is the flattened voxels of the entire volume
- 3rd dimension is each indivual streamline
Factorization of dMRI
A dMRI volume is represented as a 2D matrix \(\mathbf{Y}\) obtained by the product of the connectome matrix \(\Phi\) and a dictionary \(\mathbf{D}\) (2D matrix) of dMRI signal predictions:
\[\mathbf{D} \in \mathbb{R}^{N_\theta \times N_a} : \mathbf{Y} \approx \Phi \times_1 \mathbf{D} \times_3 \mathbf{1}\]where “\(\times_n\)”” is the tensor-by-matrix product in mode-n and the dot product with \(\mathbf{1} \in \mathbb{R}^{N_f}\) sums over the streamline dimension.
The goal is to learn \(\Phi\) directly from dMRI data.
Objective function using group regularizer
Using a maximum likelihood approach with an \(L_2\) reconstruction will lead to a dense matrix and will not enforce biological constraints.
Groups are formed using spatial coordinates (e.g. a cube of 27 voxels \(\mathcal{G_v} \in \mathcal{V}\)) and orientation similarity (\(\mathcal{G_A \in \mathcal{A}}\), formed by selecting one orientation and including all orientations within a small angle). They define \(\mathbf{x}_{\mathcal{G_A,G_V,f}}\) as a vector indicating, for all voxels \(\mathcal{v} \in \mathcal{G_v}\), whether streamline \(\mathcal{f}\) is active for any orientation \(\mathcal{a} \in \mathcal{G_a}\). They want the entire vector to be either all zeros (the streamline is not active in any of the group’s voxels), or to have more than one non-zero entry (multiple nearby voxels share the same streamline). This is encouraged using an \(l_1\) regularizer.
NOTE: In the paper, there is a trick to make this vector continuous instead of 0-1 indicators.

To reduce the number of parameters to optimize, they first choose a subset of orientations to consider in each voxel using their own “Orientation Greedy” criterion that is better designed than “Orthogonal Matching Pursuit”. Their criterion will select orientations that are similar instead of orthogonal, which is better suited to dMRI data and streamlines.
Then, subgradient descent is used to optimize the parameters, which is a convex problem after “screening” the orientations.
Experiments
Data
- “2” bundles are studied : the Arcuate Fasciculus (Arcuate) and its combination with the Superior Longitudinal Fasciculus-1 (ARC-SLF)
- Their dMRI data was generated by an expert connectome within the ENCODE model
Results
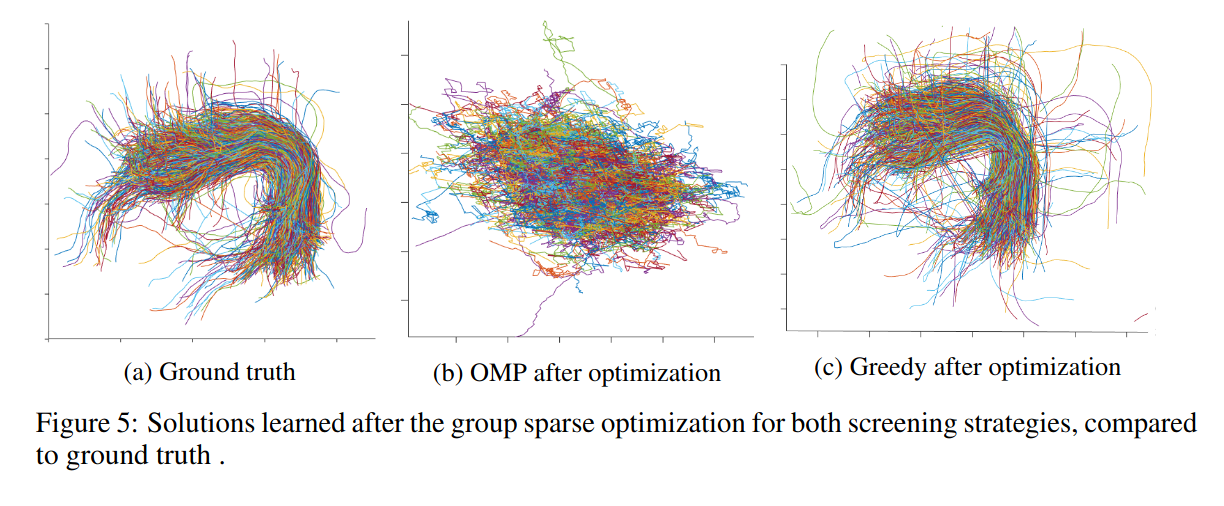
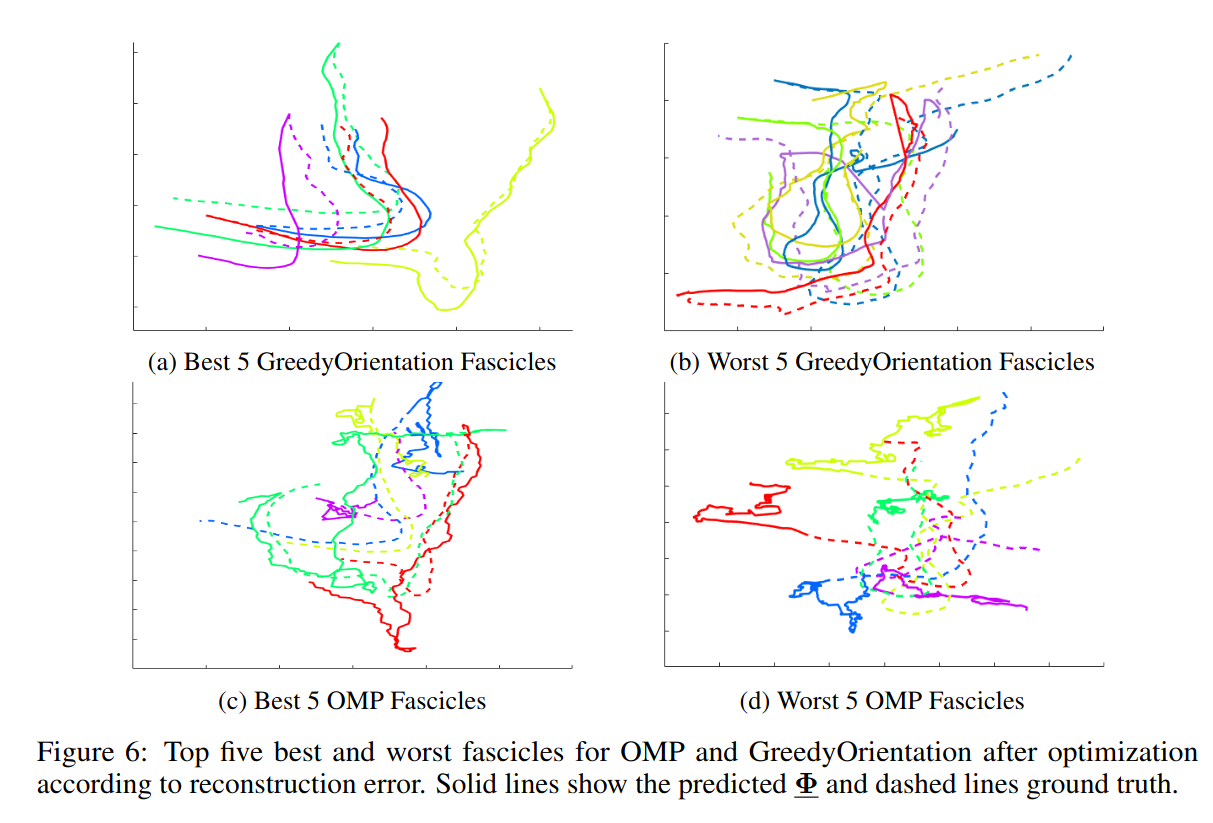
Comments
- They claim to be the first “complete data driven approach for extracting brain connectomes”
- Unclear how they choose the number of streamlines
- Unclear how they choose to focus on a single bundle