Highlights

• Novel way to formulate RL in a Supervised Learning context
• Reward is included in model input as well as other information

Introduction

While there is a rich history of techniques that incorporate supervised learning (SL) into reinforcement learning (RL) algorithms, it is believed that fully solving RL problems using SL is not possible, because feedback from the environment provides error signals in SL but evaluation signals in RL. Put simply, an agent gets feedback about how useful its actions are, but not about which actions are the best to take in any situation. On the possibility of turning an RL problem into an SL problem, Barto and Dietterich surmised: “In general, there is no way to do this.”

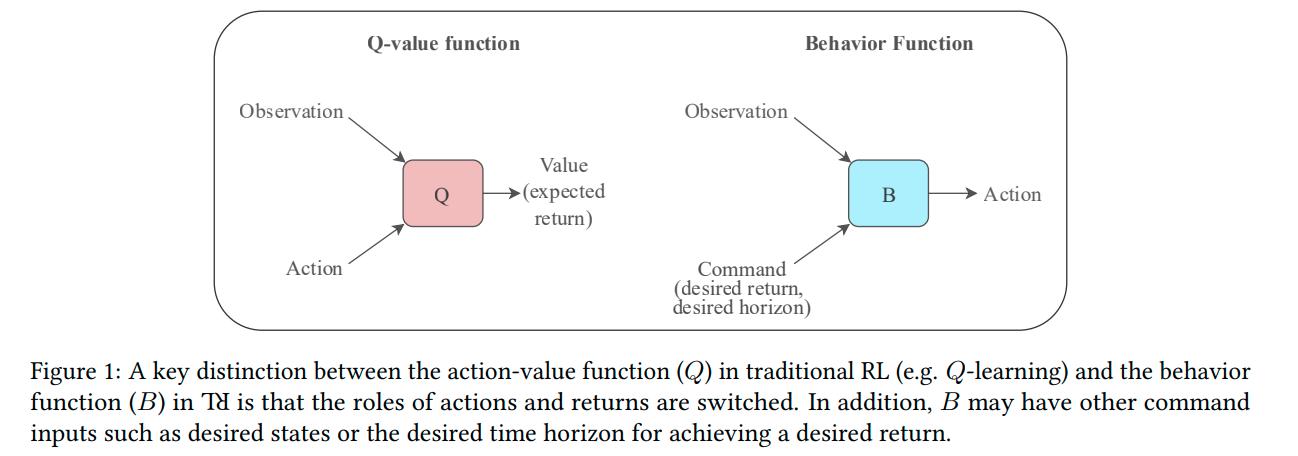
Upside-Down RL (UDRL) diverges from other attempts to formulate RL as a SL problem in that the reward, amongst other things, is now included as part as the model’s input. The model then learns to map the input, a concatenation of the current state of the environment and the desired command to actions to apply to the environment.

Methods

Formally, as usual, \(s \in S\) denotes the current states, \(a \in A\) denotes actions, \(r\) denotes rewards and \(\tau\) denotes a set of trajectories where each trajectory is defined by a list of \((s_0, a_0, r_0, s_{1}) .. (s_t, a_t, r_t, s_{t+1})\). Trajectories are sampled by a policy \(\pi\) (or behavior function \(B\)). \(c\) will denote a command, where \(c_t = (d^{r}_{t}, d^{h}_{t})\) is the command at time \(t\), \(d^r\) is the desired reward and \(d^h\) the desired horizon . According to the technical report¹, commands can also include more information as part of an \(extra_t\) vector like \(morethan_t\) where you want the behavior function to acquire more than the reward specified. The base command can be interpreted as “accumulate as much as reward in that amount of steps”.

The training can be split into two phases (that can also run simultaneously and update each other once in a while): Training (alg.1) and Gathering (alg.2)

Training is done by selecting a batch of episodes from the replay buffer, fetching only a random part of the episode, building the associated commands and using the actions as targets. To gather new episodes, the mean length of the top N episodes in the replay buffer is used as \(d^h_0\) and \(d^r_0\) is sampled from \(\mathcal{N}(M,S)\) where M and S are the mean and standard deviation of the reward of the same episodes.

Data

Tests were done on LunarLander-v2, TakeCover-v0 and LunarLanderSparse, where the reward is delayed until the last step.

Results

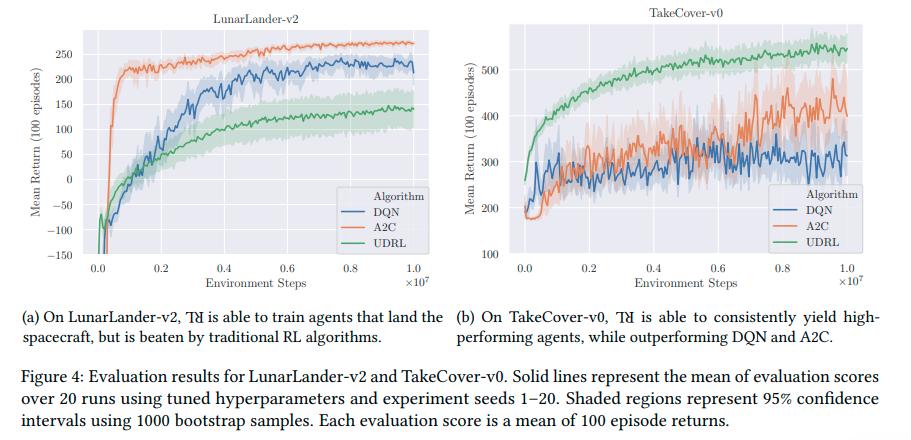
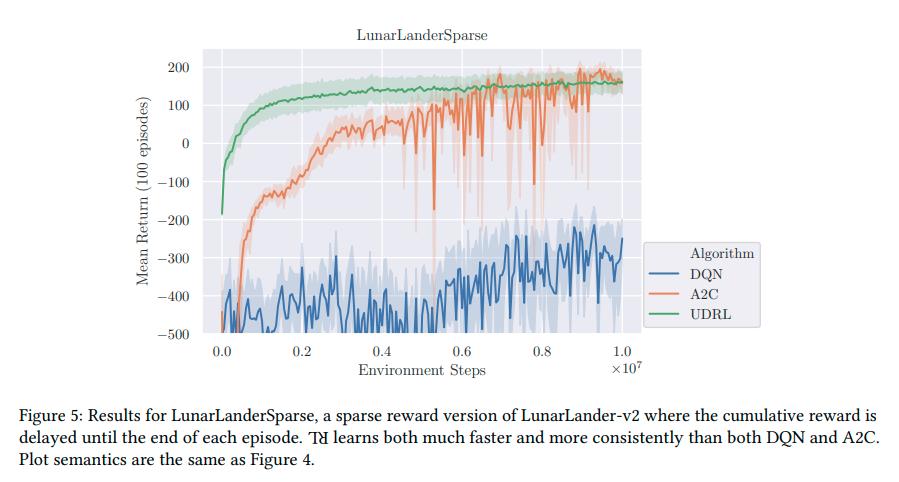
Conclusions

UDRL solves a couple of problems related to TD-Learning and infinite horizon, do not have to learn from moving targets, and more while having decent results.

Remarks

• The upside-down script used throughout the article and related technical paper is an abomination.
• The original technical report is very painful to read and half the citation are from his own articles
• UDRL is not the first to try to present RL as SL but is the first, to my very limited knowledge, to modify the input.

References

• Discussion on /r/MachineLearning: https://www.reddit.com/r/MachineLearning/comments/e8cs1y/r_reinforcement_learning_upside_down_dont_predict/; https://www.reddit.com/r/MachineLearning/comments/e86xoi/r_training_agents_using_upsidedown_reinforcement/
• Implementation (not by the authors): https://github.com/haron1100/Upside-Down-Reinforcement-Learning