Highlights

Authors present a method for brain mesh transformation matrix learning using few randomly sub-sampled nodes from the graphs.

Introduction

Current deep learning approaches for brain surface parcellation can be split into two groups:

• Those relying on the Euclidean space.
• Those relying on the Fourier domain. The spectral domain is obtained by decomposing the graph Laplacian, which captures relevant shape information. However, the spectral decomposition across different brain graphs causes inconsistencies between the eigenvectors of individual spectral domains, causing the graph learning algorithm to fail.

Current spectral graph convolution methods handle this variance by separately aligning the eigenvectors to a reference brain in a slow iterative step.

Authors present a Spectral Graph Transformer (SGT) network that uses very few randomly sub-sampled nodes in the spectral domain to learn the alignment matrix for multiple brain surfaces.

Methods

The spectral decomposition of the brain graph is randomly sub-sampled as an input point cloud to a SGT network. The SGT learns the transformation parameters aligning the eigenvectors of multiple brains. The transformation matrix is multiplied with original spectral coordinates to feed the Graph Convolutional Netowrk (GCN) for brain surface parcellation purposes.

• Firstly, the cortical surfaces modeled as brain graphs are embedded in a spectral manifold using the graph Laplacian operator.

• Secondly, graph nodes are randomly sampled in the spectral embeddings and fed to the SGT network to align the brain embeddings.

• Finally, a GCN provides a labeled graph as output, taking spectral coordinates and cortical sulcal depth as input.

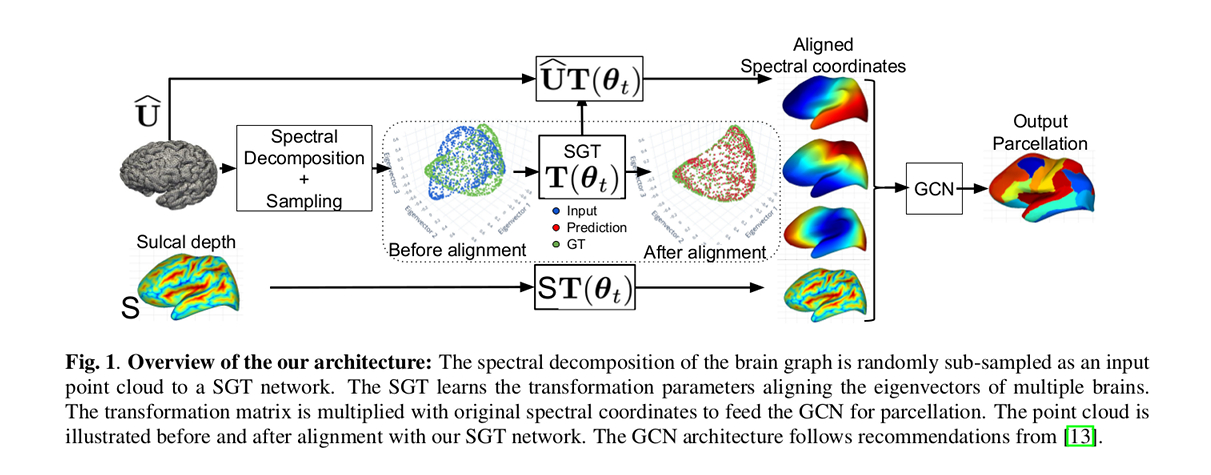
where \(\hat{\mathbb{U}}\) are the normalized spectral coordinates; \(\mathbb{T}\) is the transformation matrix for every brain graph.

The surface convolution expression is given by:

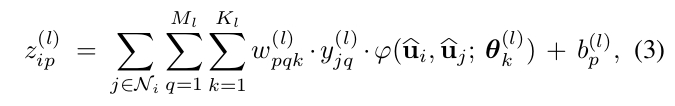
where \(\phi\) is a symmetric kernel in the embedding space with parameters \(\theta_{k}\). Authors use a Gaussian kernel, i.e. the parameters \(\theta_{k}\) are the mean and the standard deviation.

The loss has two terms:

• The Spectral Transformer loss: the mean square error between the obtained predicted coordinates and spectral coordinates \(\tilde{\mathbb{U}}\) with the iterative alignment method. To enforce regularization during training, and match the possible rotation and flip ambiguity of eigen decomposition, they impose the transformation matrix to be orthogonal.
• The GCN loss.

Data

The Mindboggle ¹ dataset containing 101 manually-labeled brain surfaces was used.

The training/validation/testing split was 70-10-20%.

Results

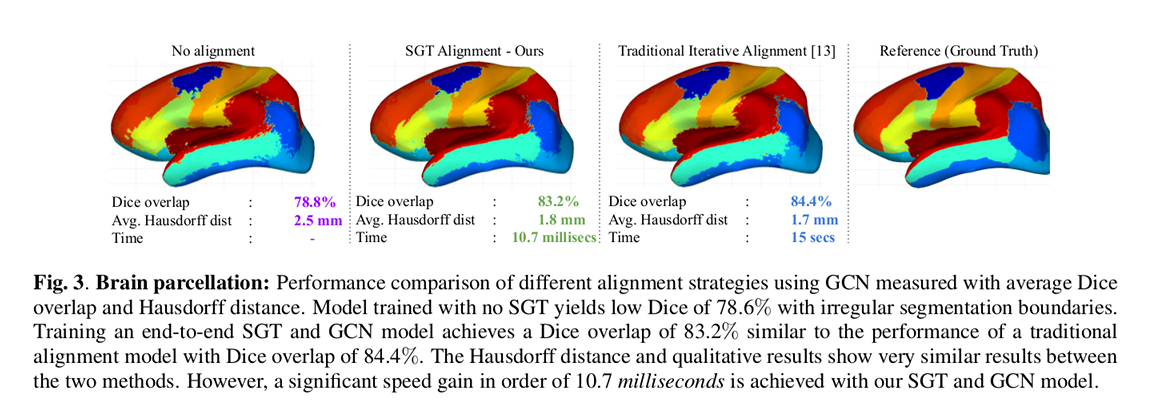
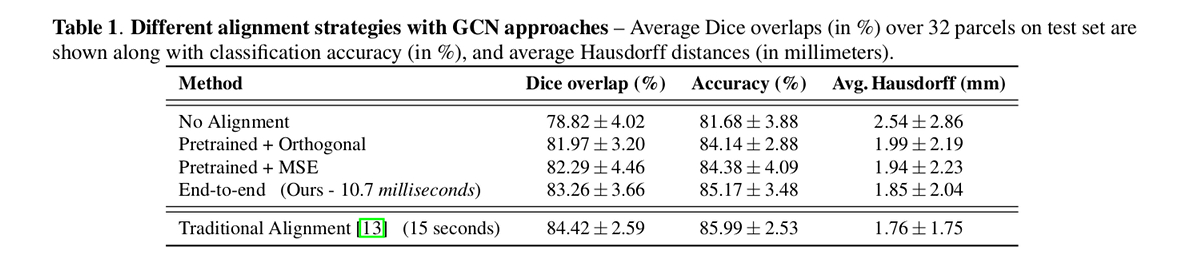
Authors’ results show that their approach achieves similar performance compared to the iterative approach but uses three orders of magnitude less time at test time.

Conclusions

The paper presents an end-to-end framework for learning a spectral transformation required for graph convolution networks.

Comments

• It is unclear how the output parcellation is achieved using just the sulcal depth as input.

• Related to the the MIDL 2019 paper by the same last three authors.

References