Associative Compression Networks for Representation Learning
Highlights
- Current VAEs have the shortcoming of ignoring latent codes because of powerful decoders
- Novel framework for variational autoencoding with neural networks: Associative Compression Networks (ACN)
Introduction
The authors explain that compact, transferable representations will benefit the full spectrum of cognitive tasks. They also explain that the current variational autoencoders (VAEs) have some shortcomings when it comes to representation learning. As such, they state that sufficiently powerful decoders will simply ignore the latent codes and learn an unconditional model of the data. They mention various modifications to VAEs proposed to correct this, but explain that these modifications add parameters to the system that must be tuned by hand. The modifications also lead to worse log-likelihoods than purely autoregressive models.
The authors dive into detailed explanations about the encoding process in VAEs and how we can analyze it through information theory. Their main takeaway is that VAEs lead to a paradigm where latent codes are used to organize the training set as a whole, rather than annotate individual training examples. They posit that we could get a more efficient encoding, and better separation between high-level representation and low-level details, by preserving some kind of ordering in the space.
Methods
Similarity and ordering of the data
If we acknowledge a varying prior in the latent space for different samples, the optimal ordering minimizes the sum of the KLs when encoding each sample. The authors state that this optimal ordering is well approximated by \(K\) nearest neighbor sampling.
Associative Compression Networks
Given that we now know a way to approximate the optimal ordering, the goal is to integrate this knowledge into the training process of a VAE. Thus, the main difference between ACNs and traditional VAEs is that ACNs use a prior network (MLP) to condition, for each sample, the prior on a code chosen from the \(K\) nearest neighbors in latent space to the current encoding. A unit variance, diagonal Gaussian, was also used for all encoding distributions, meaning that every encoding is entirely described by its mean vector.
Thus, we can formulate ACNs’ loss as follows, here compared to how we could express the traditional VAE loss:
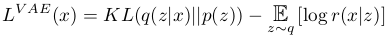
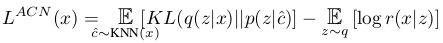
The term \(p( z | \hat{c} )\) includes the prior network, that parametrizes the prior conditioned on a random from within the \(K\) nearest neighbors of the current encoding. The prior is parameterized from the outputs of the prior network as follows:
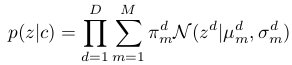 ,
,
where \(\pi^{d}_{m}\), \(\mu^{d}_{m}\) and \(\sigma^{d}_{m}\) are emitted by the prior network (with some normalization applied afterwards).
The conditioning on neighboring codes is equivalent to a sequential compression algorithm (i.e. the ordering mentioned previously), as long as every neighbor is unique to a particular code. This can be ensured by a simple constraint on the training procedure: restrict KNN(\(x\)) at each step to contain only codes that have not yet been used as neighbors during the current pass through the dataset.

Sampling
The use of conditional priors opens up an alternative sampling protocol, where sequences of linked samples are generated from real data by iteratively encoding the data, sampling from the prior conditioned on the code, generating new data, then encoding again. These sequences are referred to as ‘daydreams’.
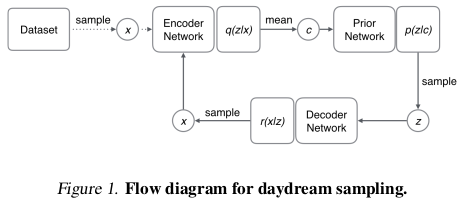
Other sampling methods to get a sense of the features represented in the latent space are detailed in the paper.
Results
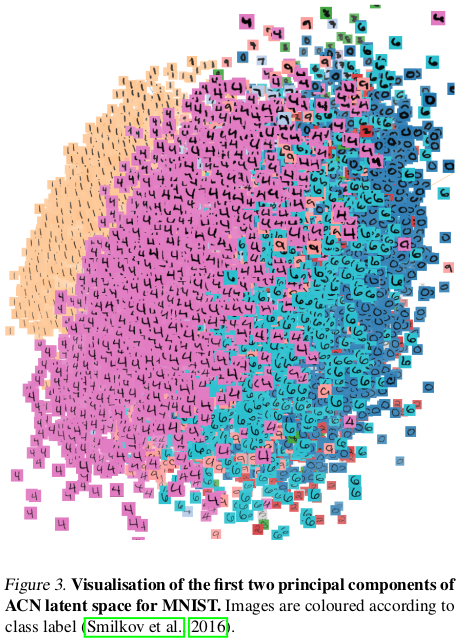
A lot of experiments on MNIST are explained in the paper, showcasing both the compression results and representation learned. Reconstructions and daydream results are also illustrated for CIFAR-10, ImageNet and CelebA. Presented here are only a few hand-picked results deemed most relevant.
Compression
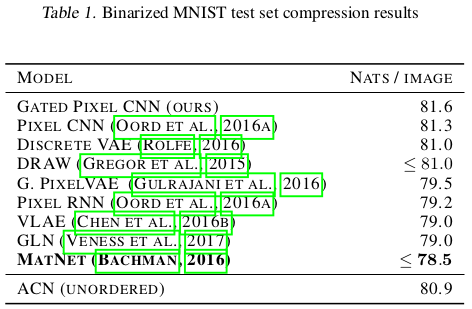
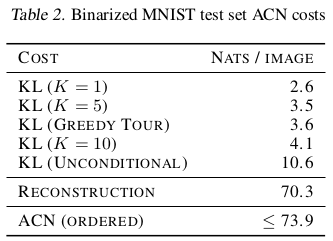
Representation

Reconstruction



Conclusions
The authors hope their work will open the door to more holistic, dataset-wide approaches to generative modelling and representation learning.
Remarks
- No ablation study is provided as to why a full-blown neural network is required to condition the prior for a sample’s encoding on its nearest neighbor in the latent space.