Introduction

Energy-Based Memory Models (EBMM) is an approach to the problem of associative memory. The goal is being able to retrieve a remembered data point from a distorted or incomplete version.

Associative Memory

In a less neuroscientific language, and in a more machine learning oriented language, the task is pretty much “overfitted inpainting”.

First, a fixed-size batch of data points (e.g. images) are written to memory. Then, given a distorted version of a stored data point, we want to reconstruct the original.

While this kind of problem is often approached using VAEs or GANs, the authors propose a significantly different method.

Method

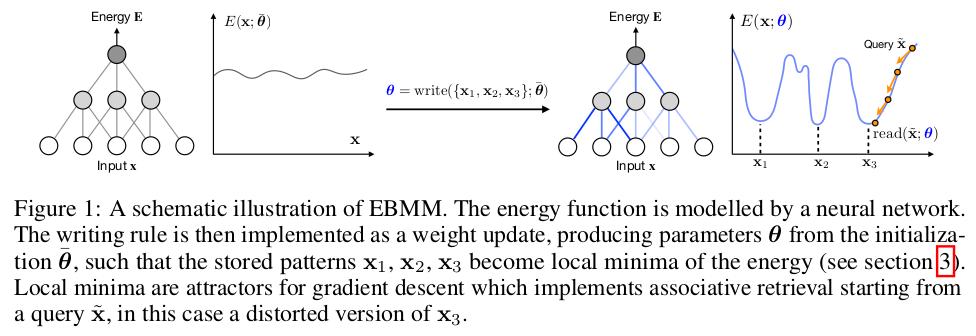
With EBMM, the weights of a neural networks are used as the memory. The input of the model is a data point (e.g. image), and the output is an energy value. A stored data point corresponds to a local minima of this energy function, i.e. all inputs similar to a stored memory have a higher energy.

Reading

To retrieve a data point, we optimize the input by minimizing the energy with respect to the input. The weights remain fixed, as they represent the memory. In theory, the data point is retrieved successfully when the optimization converges. In practice, 5 steps are taken. This type of network is called an “attractor network”.

Writing

The writing process consists in optimizing the weights of the network, so that the reading process produces good reconstructions. This writing/reading process is learned through meta-learning, by performing many write and read optimization procedures (with a small number of iterations) for several sets of write and read observations. The reconstruction error is then backpropagated through all these sub-optimizations.

Results

The proposed method is more efficient than the state of the art for storing high complexity data points like images. However, for lower complexity such as Omniglot characters, the advantage is less clear.

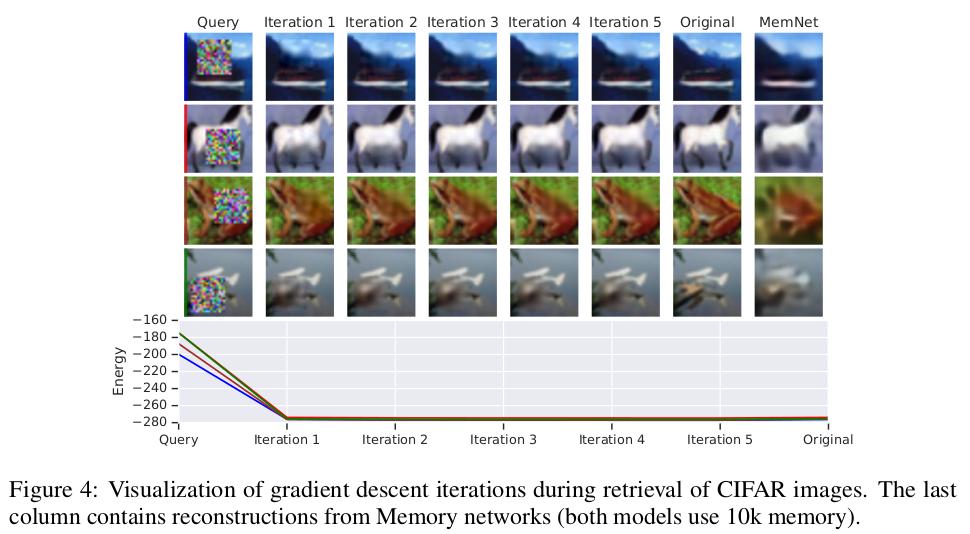
The figure below exemplifies the retrieval process. As you can see, most of the job happens in the first step.

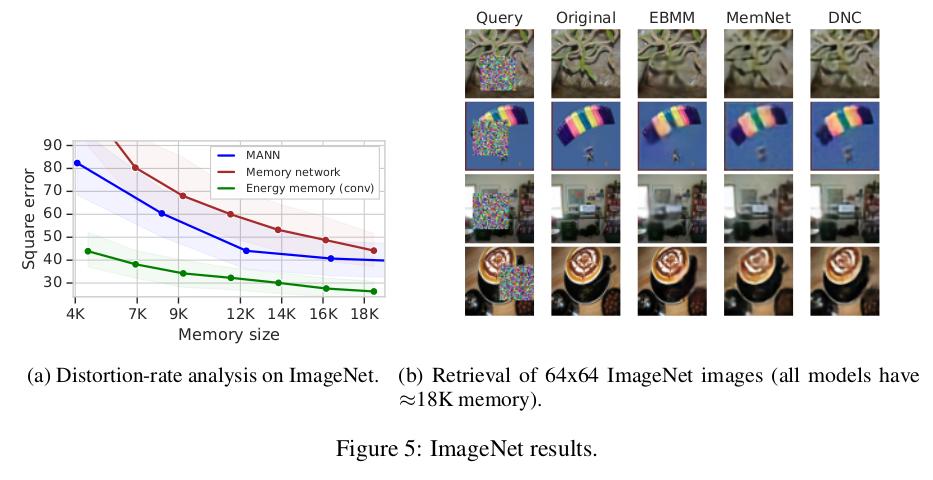
The figure below compares EBMM with other methods, i.e. Memory-Augmented Neural Network, Memory Networks and Differentiable Neural Computer. The plot compares efficiency, and the grid shows reconstruction results.

Discussion

• Authors say that “more elaborate architecture search could lead to stronger results on par with state-of-the-art generative models”
• EBMM forces batch writing
• EBMM reading is not stochastic, which can introduce blur in the presence of uncertainty
• Authors say that they had to decrease the batch size for the ImageNet experiment because of prohibitively expensive computations. (They work at DeepMind.)

Conclusion

In itself, this work is more interesting from a theoretical standpoint, but it could motivate new research into applying attractor networks to concrete problems.