The authors propose a new type of convolution module, Octave Convolution, which can replace convolution modules in most CNNs. The goal is to have coarse and fine features in a single convolutional layer. Leveraging coarse features using a smaller resoluton yields FLOPs and memory savings.

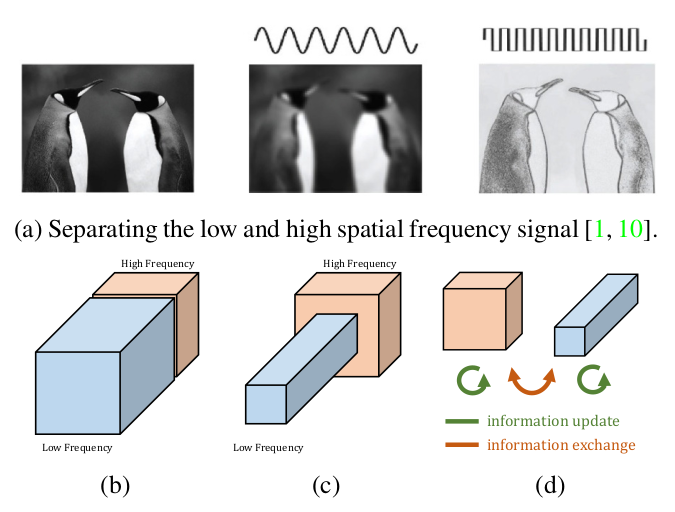
In a peanutshell: a number of feature maps are created with a resolution that is half the resolution of the others (here, “octave” means a scale factor of 2), low and high resolution feature maps are summed together to enable processing in two regions of the frequency spectrum.

Method

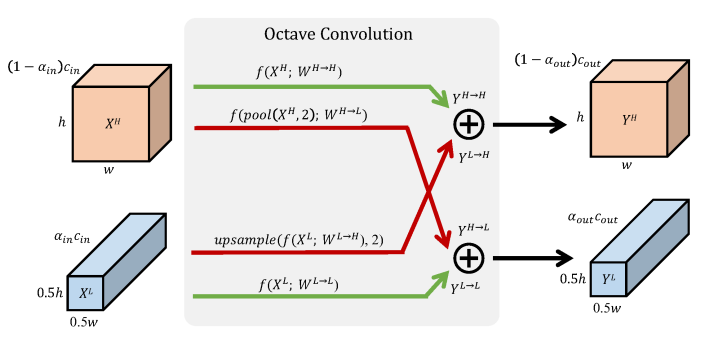
There are two types of feature maps: high resolution (H), and low resolution (L). Hyperparameter \(\alpha \in [0,1]\) is the proportion of L feature maps.

Instead of a single weight tensor \(W\) in the original convolution module, there are 4 in the OctConv: \(W^H, W^L, W^{H \rightarrow L}, W^{L \rightarrow H}\). This means that there are 4 “vanilla convolutions” inside an Octave Convolution.

As you can see in the figure below, \(Y^H\) (the high resolution output feature maps) is the sum of two tensors; one coming from \(X^H\), the other coming from \(X^L\). To make the tensors compatible for summation, pooling and upsampling is used.

In pseudocode:

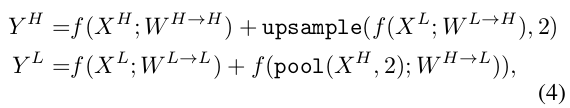
Results

In some cases, OctConv manages to reduce the FLOPs while also improving accuracy.

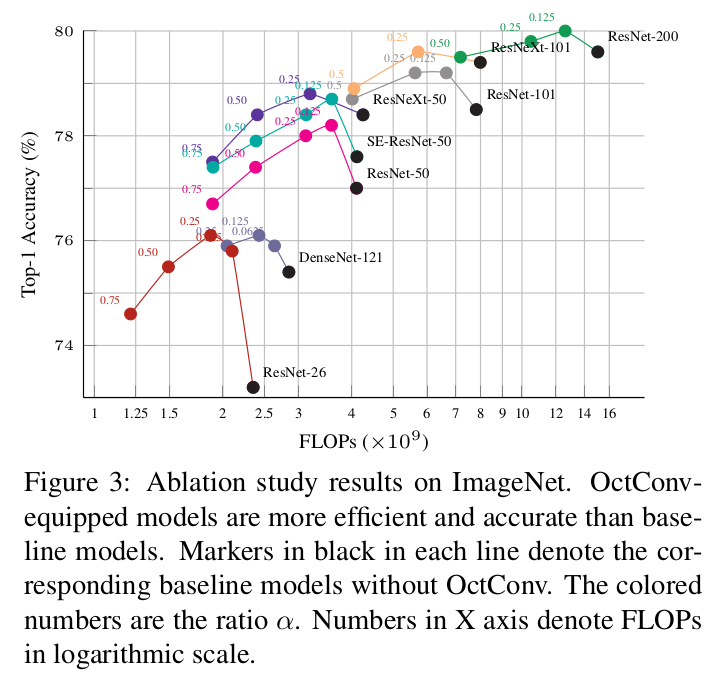
In other cases, OctConv offers a trade-off between latency and accuracy:

The authors explain the performance with the increased receptive field allowed by the low resolution feature maps, and the reduction of “spatial redundancy”. We could also hypothesize that the more efficient structure allows to reduce overfitting.

Caveats

Stupid Fourier experiment that probably invalidates the frequency separation claim. They perform a Fourier transform of some feature maps (unclear what data, what architecture) to prove that OctConv separates high and low frequencies. However, the low resolution maps are low frequency by construction! I suppose that they upsampled those feature maps before computing the Fourier transform (it’s not explained); if that’s the case, no wonder why there are no high frequencies! In addition, the spectrum produced for the high resolution maps looks almost exactly like the spectrum of the baseline (vanilla conv): there is an energy peak at the lowest frequencies! This seem to invalidate their claim that OctConv separates low and high frequencies.
Questionable claims:
- “We propose to factorize convolutional feature maps into two groups at different spatial frequencies and process them with different convolutions at their corresponding frequency” (Frequency separation has not been clearly proven)
- “We design a plug-and-play operation named OctConv to replace the vanilla convolution for operating on the new feature representation directly and reducing spatial redundancy” (Reduction of the spatial redundancy has not been clearly proven, nor explained)
- “We attribute the increase in accuracy to OctConv’s effective design of multi-frequency processing and the corresponding enlarged receptive field which provides more contextual information to the network”
- “At test time, the gain of OctConv over baseline models increases as the test image resolution grows because OctConv can detect large objects better due to its larger receptive field”
- “Octave Convolution can also improve the recognition performance by effective communication between the low- and high-frequency and by enlarging the receptive field size which contributes to capturing more global information”
- “Compared to the closely related Multi-grid convolution [25], OctConv provides more insights on reducing the spatial redundancy in CNNs based on the frequency model and adopts more efficient interfrequency information exchange strategy with better performance.”
Questionable horizontal separator in table 5.