Synergistic Image and Feature Adaptation Towards Cross-Modality Domain Adaptation for Medical Image Segmentation
Code avalable: https://github.com/cchen-cc/SIFA
Introduction
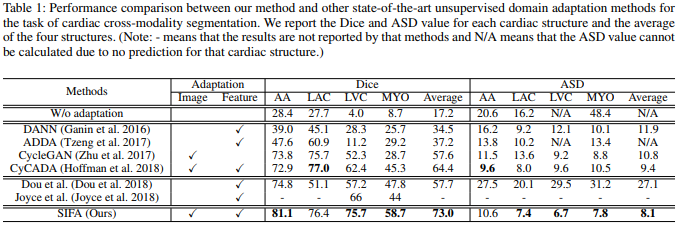
This paper presents an unsupervised domain adaptation framework, called Synergistic Image and Feature Adaptation (SIFA). SIFA is a learning diagram which presents a synergistic fusion of adaptations from both image and feature perspectives. They simultaneously transform the appearance of images across domains and enhance domain-invariance of the extracted features towards the segmentation task. Without using any annotation from the target domain (CT images), the model is guided by adversarial losses, with multiple discriminators employed from various aspects. They validated this method with a challenging application of cross-modality medical image segmentation of cardiac structures. The results demonstrate that SIFA model recovers the degraded performance from 17.2% to 73.0%, and outperforms the state-of-the-art methods.
This method transforms the labeled source images (MR images) into the appearance of images drawn from the target domain (CT images), by using generative adversarial networks with cycle-consistency constraint. When using the synthesis target-like images to train a segmentation model, they integrate feature adaptation to combat the remaining domain shift. Two discriminators are used to connecting the semantic segmentation predictions and generated source-like images, to differentiate whether obtained from synthesis or real target images. Like the following image show, the model shares the feature encoder, such that it can simultaneously transform image appearance and extract domain-invariant representations for the segmentation task.
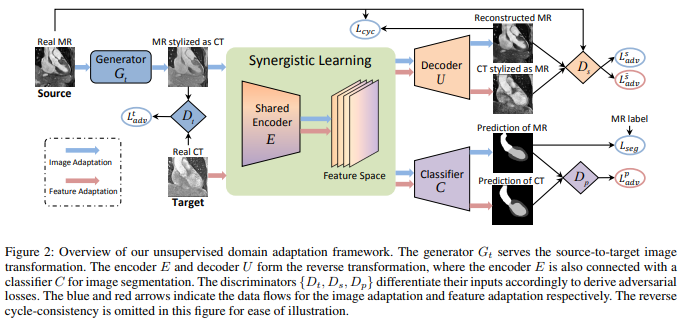
The entire domain adaptation framework is unified, and both image and feature adaptations are seamlessly integrated into an end-to-end learning diagram. The contributions of this paper are:
- An unsupervised domain adaptation framework that exploits synergistic image and feature adaptations to tackle domain shift via complementary perspectives.
- They enhance feature adaptation by using discriminators in two aspects, semantic prediction space and generated image space. Both compact spaces help to enhance domain-invariance of the extracted features further.
Methods
Image Adaptation for Appearance Alignment
They aim to transform the source images \(x^s\) towards the appearance of target ones \(x^t\), which hold different visual appearance due to domain shift. The obtained transformed image looks as if drawn from the target domain, while the original contents with structural semantics remain unaffected. Briefly speaking, this module narrows the domain shift between the source and target domains by aligning image appearance.
In practice, they use generative adversarial networks, which have made a wide success for pixel-to-pixel image transformation, by building a generator \(G_t\) and a discriminator \(D_t\). The generator aims to transform the source images to target-like ones \(G_t(x^s) = x^{s\rightarrow t}\). The discriminator competes with the generator to correctly differentiate the fake transformed image \(x^{s\rightarrow t}\) and the real target image \(x^t\). The \(G_t\) and \(D_t\) form a minimax two-player game and are optimized via the adversarial learning:
\[\mathcal{L}^{t}_{adv}(G_t,D_t)=\mathbb{E}_{x^t \sim X^t}[ \log D_t (x^t)] + \mathcal{E}_{x^s \sim X^s}[ \log (1-D_t(G_t(x^s)))]\]The encoder \(E\) and upsampling decoder \(U\) form the reverse target-tosource generator \(G_s = E \circ U\) to reconstruct the \(x^{s\rightarrow t}\) back to the source domain, and a discriminator \(D_s\) operates in the source domain. This pair of source \(\{G_s, D_s\}\) are trained in the same manner as \(\{G_t, D_t\}\) with the adversarial loss \(\mathcal{L}^s_{adv}\).
Then the pixel-wise cycle-consistency loss \(\mathcal{L}_{cyc}\) is used for recovering the original image:
\[\mathcal{L}_{cyc}(G_t, E, U)= \mathcal{E}_{x^s \sim X^s}\parallel U(E(G_t(x^s))) - x^s \parallel_1 + \mathcal{E}_{x^t \sim X^t}\parallel G_t(U(E(x^t))) - x^t \parallel_1\]With the adversarial loss and cycle-consistency loss, the image adaptation transforms the source images into target-like images with semantic contents preserved.
The composition of \(E\circ C\) serves as the segmentation network for the target domain, and the segmentation loss is defined as:
\[\mathcal{L}_{seg}(E,C)=H(y^s, \hat{y}^{s\rightarrow t}) + \alpha \cdot Dice(y^s, \hat{y}^{s\rightarrow t})\]The first part represents a cross-entropy loss, and the second part is the Dice loss with a regulator \(\alpha\) (trade-off hyper-parameter) balancing those two. The hybrid loss function is designed to meet the class imbalance in medical image segmentation.
Feature Adaptation for Domain Invariance
To make the extracted features domain-invariant, they choose to enhance the domain-invariance of feature distributions by using adversarial learning via two compact lower-dimensional spaces. For the prediction of segmentation mask, the discriminator \(D_p\) classify the outputs corresponding to \(x^{s\rightarrow t}\) or \(x^t\). The semantic prediction space represents the information of human-body anatomical structures, which should be consistent across different imaging modalities. The adversarial loss from semantic-level supervision for the feature adaptation is:
\[\mathcal{L}_{adv}^p(E, C, D_p)= \mathcal{E}_{x^{s\rightarrow t} \sim X^{s\rightarrow t}}[\log D_p(C(E(x^{s\rightarrow t})))] + \mathcal{E}_{x^t \sim X^t}[\log (1-D_p(C(E(x^t)))]\]They add an auxiliary task to the source discriminator \(D_s\) to differentiate whether the generated images are transformed from real target images or a reconstructed one. To make the features domain-invariant, this adversarial loss is employed to supervise the feature extraction process:
\[\mathcal{L}_{adv}^{\tilde{s}}(E, D_s)= \mathcal{E}_{x^{s\rightarrow t} \sim X^{s\rightarrow t}}[\log D_s(U(E(x^{s\rightarrow t})))] + \mathcal{E}_{x^t \sim X^t}[\log (1-D_s(U(E(x^t)))]\]Synergistic Learning Diagram
Importantly, a key characteristic in this proposed synergistic learning diagram is to share the feature encoder \(E\) between both image and feature adaptations. The overall objective for the framework is as follows:
\[\mathcal{L} = \mathcal{L}^{t}_{adv}(G_t, D_t) + \lambda^{s}_{adv} \mathcal{L}_{adv}^{s}(E, U, D_s) + \lambda_{cyc} \mathcal{L}_{cyc}(G_t, E, U) + \lambda_{seg} \mathcal{L}_{seg}(E, C) + \lambda^{p}_{adv} \mathcal{L}_{adv}^{p}(E, C, D_p) + \lambda^{\tilde{s}}_{adv} \mathcal{L}^{\tilde{s}}_{adv}(E, D_s)\]Where the lambdas are trade-off parameters.
Results