Overview

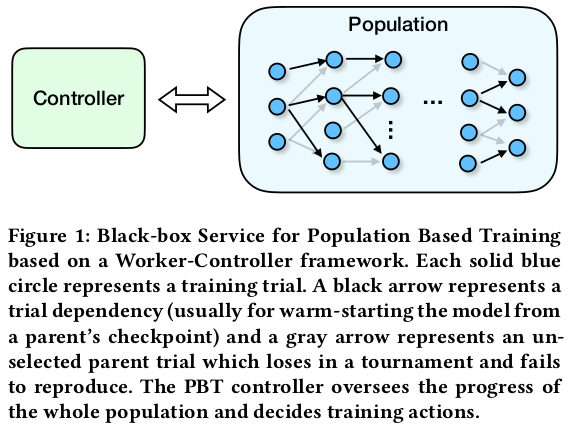
The authors present a population based training (PBT) method for optimizing hyperparameters while training the parameters of the model. The method is based on evolution, and uses “trials”. A trial is a small chunk of training that has a warm-start using parameters from a previous trial.

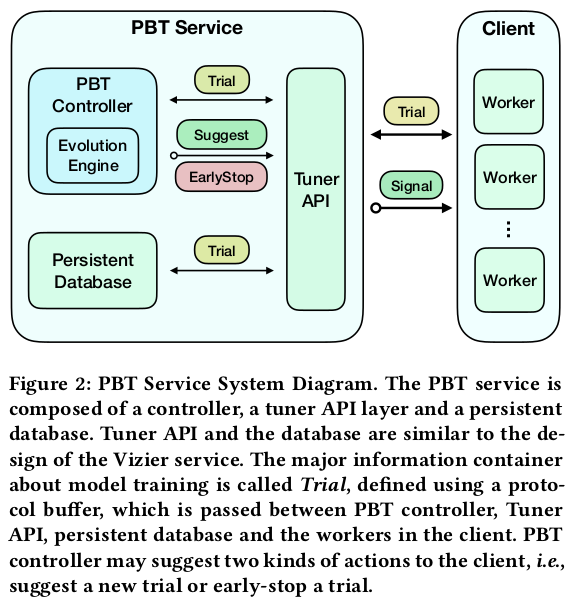
This is considered “black box hyperparameter optimisation”, because the method does not need to know about the network architecture. The only requirement is that the network can be warm-started by loading weights, and that performance of the network can be measured.

Method

Run \(N\) trials in parallel, where a trial is \(S\) steps of training; each trial has different hyperparameters
Evaluate the networks produced
Select the \(M \lt N\) networks that will reproduce
Mutate the hyperparameters of the parents to produce a total of \(N\) children (children = trial)
Return to 1, until the allowed compute time is elapsed

Note that child trials start with the checkpoint from their parent.

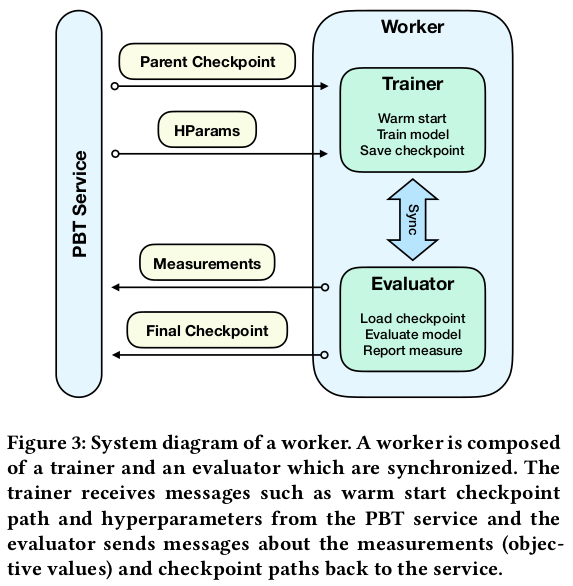
Here, there is one worker per child (number of workers = population size), but the paper describes a “budget mode” where a larger population can be used. See sections 3.7 and 3.10 for practical details.

Experiments

The authors claim to have trained a state-of-the-art WaveNet for voice synthesis using their proposed method (PBT). They only optimize the learning rate! This means that their method can be seen as optimising the learning rate schedule.

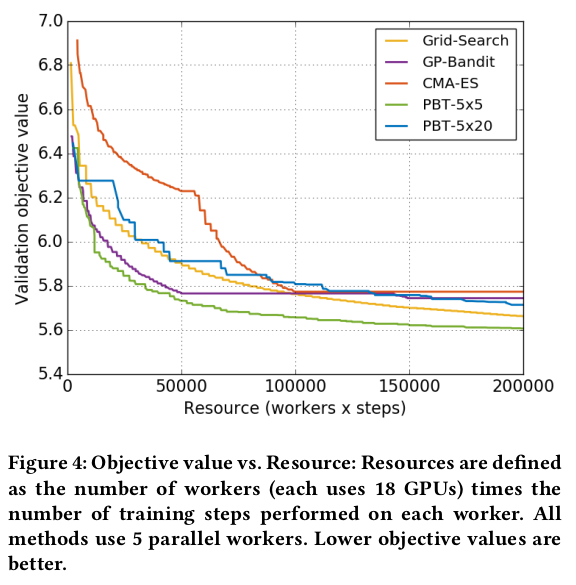
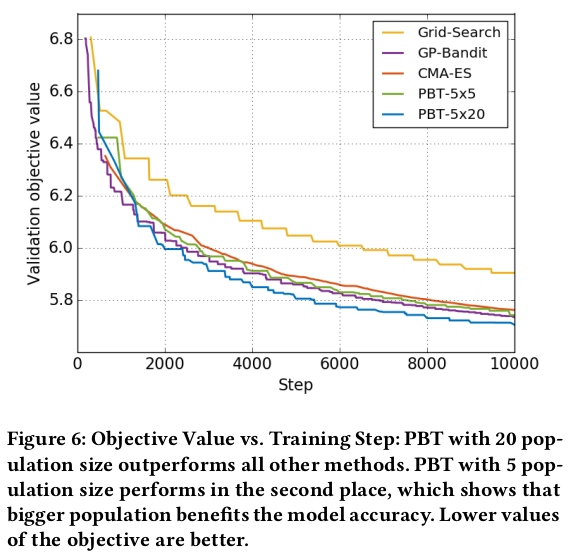
PBT can converge faster than others, if the number of workers and population size is well chosen. In addition, PBT has less variance than random search, as shown in Fig. 10.

In the figures below, PBT-5x5 means that there are 5 parallel workers and a population of 5; while PBT-5x20 means that the population is 20.

The following figure shows that PBT-5x5 is the most efficient in terms of compute. The next figure shows that PBT-5x20 produces better results at a given iteration.