Cortical Surface Parcellation using Spherical Convolutional Neural Networks
Highlights
Authors present a cortical surface parcellation method using spherical deep convolutional neural networks (CNNs).
Key contributions include
- Novel features optimized over cortical parcel boundaries.
- Data augmentation driven by their intermediate deformation fields.
Their method outperforms traditional multi-atlas and naive spherical U-Net approaches.
Introduction
For region-based morphological analysis, cortical surfaces need to be consistently subdivided into regions based on cortical parcellation protocols. Consistent labeling of cortical regions is challenging due to the complicated cortical folds and inter-subject variability.
Multi-atlas cortical parcellation approaches tend to provide better performance as the number of atlases increases. Unfortunately, inter-subject registration is unavoidable in this approach to align multiple atlases.
Traditional CNN architectures are still immature in handling non-uniform data with high complexity due to the Euclidean space coherence incorporated with existing deep architectures.
Spherical CNNs have recently emerged to deal with spherical domain data. The authors propose a novel cortical parcellation approach using a deep spherical U-Net encoding surface mesh features.
Methods
To compute the input features to the CNN, the following features are computed:
- The deformation field: a spherical surface registration method that reconstructs the deformation field by a linear combination of spherical harmonics coefficients (with degrees \(l=0 \ldots 10\)).
- The boundary map: deformation fields that align parcel boundaries for a more accurate prediction.
The deformed data features used to feed to the network are then:
- The mean curvature ($$$iH$) from inflated surface.
- The sulcal depth (\(SD\)).
- The mean curvature from cortical surface (\(H\)).
To create a template, they co-register training samples in an iterative manner and compute a distance map of the mode (most frequent) cortical labels across the training set after their registration to the template using the three geometric features. They then register the normalized distance map to the template distance map to produce the deformation fields.
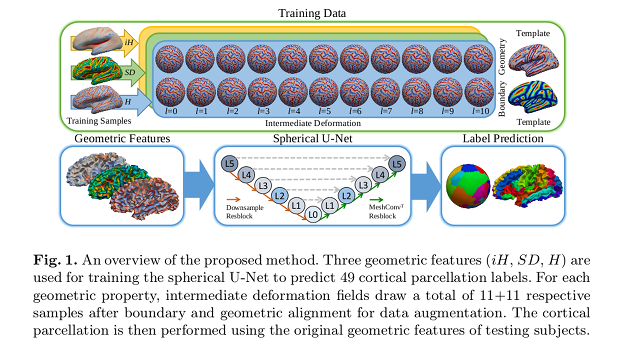
The authors used a spherical U-net architecture designed for segmentation tasks. They provide the described geometric features to the input channels and the corresponding labels to the output channels.
Data augmentation is performed by using all the deformations of the spherical harmonics between \(l=0 \ldots 10\).
At the end of the testing stage, they refine predicted parcellation maps with a standard graph-cut method to remove potential isolated regions and to create smooth parcel boundaries.
Data
427 T1-weighted 3T MRI images.
Results
The cortical surfaces and their spherical mappings were reconstructed via a standard FreeSurfer pipeline.
The baselines used were:
- A spherical U-Net model driven only by non-rigid deformation information.
- A multi-atlas and spherical U-Net model with the rigid deformation information.
For a fair comparison, the same graph-cut technique was applied to all the baseline methods.
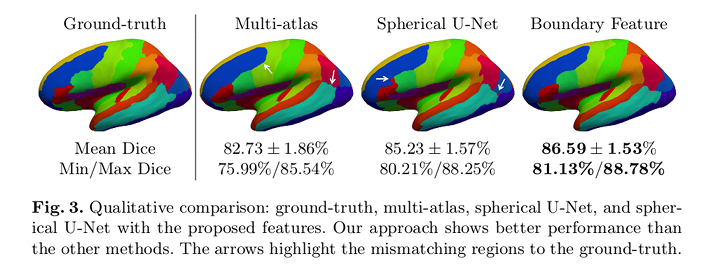
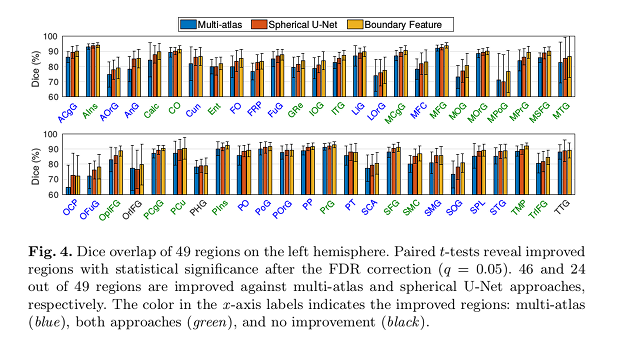
The authors’ approach outperforms multi-atlas (46 regions) and spherical U-Net (24 regions).
No regions were found with significantly reduced Dice overlap.
Conclusions
The authors presented a cortical parcellation method using a spherical U-Net with novel features optimized over cortical parcellation boundaries.
The proposed method achieves qualitatively and quantitatively better performance compared to the baselines used.