Code available here.

This paper proposes a Multi-Task Attention Network (MTAN), an architecture that can be trained end-to-end and can be built upon any feed-foward neural network is simple to implement, as well as parameter efficient.

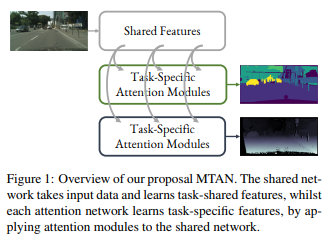
Introduction

The authors want to perform multiple tasks simultaneously to avoid training an independent network for each task, not only is this approch is more efficient in terms of memory and inference speed, but also seems that related tasks share informative visual features. Compared to standard single-task learning, training multiple task whilst succesfully learning a shared representation poses two challenges: How to share in a network architecture, and how to balance the tasks between loss functions.

The proposed configuration allows image-to-image dense pixel-level prediction, like semantic segmentation, depth estimation, and surface normal prediction.

Multi-Task Attention Network

Architecture Design

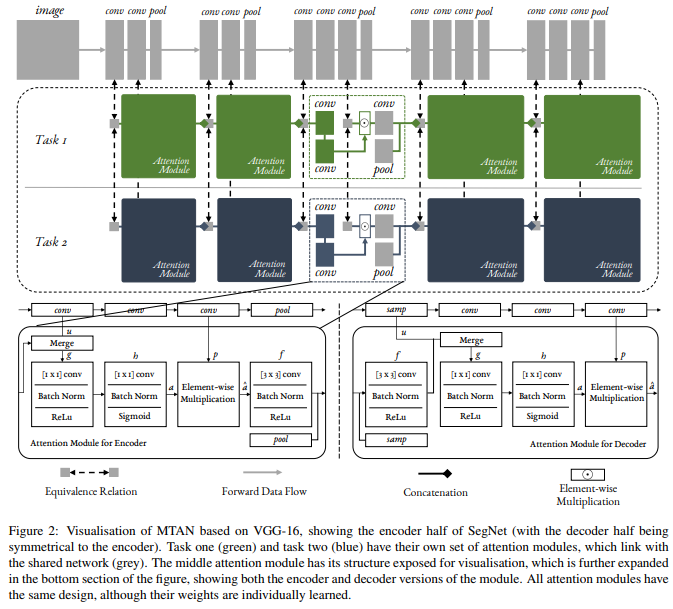
MTAN consists of a single shared network, and K task-specific attention networks. The shared network can be designed based on the particular task, whilst each task-specific network consists of a set of attention modules linked with the shared network. Therefore, the features in the shared network, and the soft attention masks, can be learned jointly to maximise the generalisation of the shared features across multiple tasks, whilst simultaneously maximising the task-specific performance due to the attention masks.

Task Specific Attention Module

The attention module is designed to allow the task-specific network to learn task-related features, by applying a soft attention mask to the features in the shared network, with one attention mask per task per feature channel. The task-specific features in this layer, are then computed by element-wise multiplication of the attention masks with the shared features.

Losses

This architecture combines a total of three losses via a weighted linear combination. The first loss is for the semantic segmentation, and it’s a simple cross-entropy loss over all classes. The second loss is for the depth estimation, where they use an \(L_1\) norm comparing the predicted and the ground-truth depth. The last one is for the surface normals, only use for the NYUv2 dataset, where an element-wise dot product is use for each normalised pixel with the ground-truth map.

Baselines

• Single-Task, One Task: The vanilla SegNet for single task learning.
• Single-Task, STAN: A Single-Task Attention Network, where we directly apply our proposed MTAN whilst only performing a single task.
• Multi-Task, Split (Wide, Deep): The standard multitask learning, which splits at the last layer for the final prediction for each specific task. We introduce two verions of Split: Wide, where we adjusted the number of convolutional filters, and Deep, where we adjusted the number of convolutional layers, until Split had at least as many parameters as MTAN.
• Multi-Task, Dense: A shared network together with task-specific networks, where each task-specific network receives all features from the shared network, without any attention modules.
• Multi-Task, Cross-Stitch: The Cross-Stitch Network¹, a previously proposed adaptive multi-task learning approach, which we implemented on SegNet.

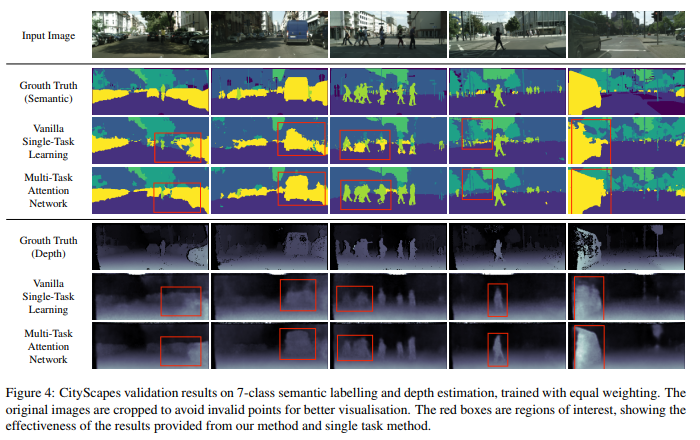
Results

References