Introduction

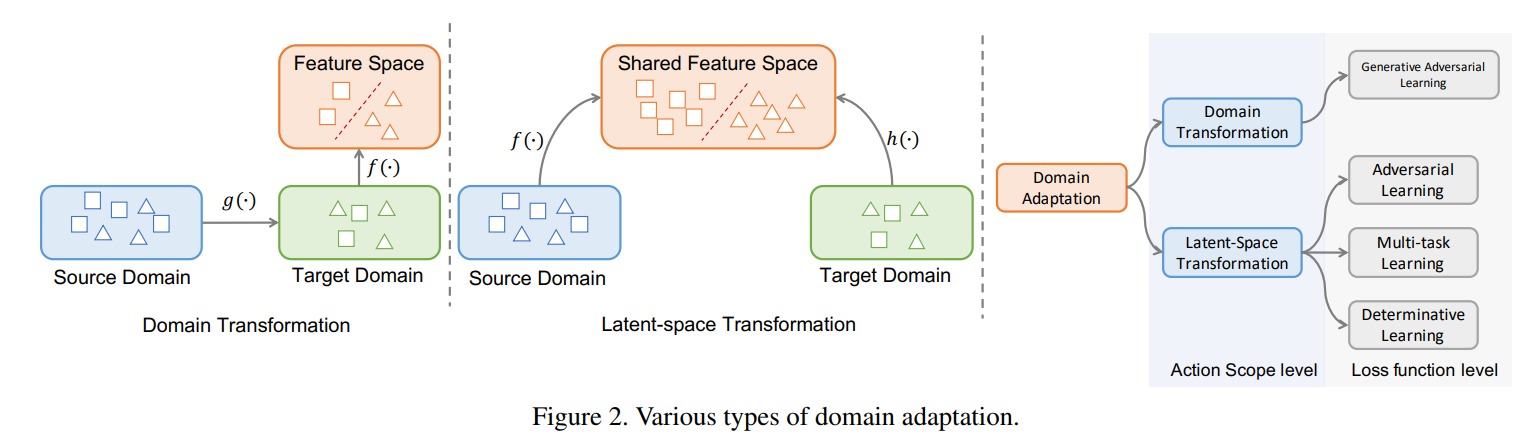
The authors propose a simple domain adaptation method which corresponds to a latent-space transformation approach (c.f.Fig.2)

Methods

The idea is very straight forward. Considering \(\Phi(.)\) a neural network projecting an input signal \(x_i\) to a latent space, they assume that a source and a target input signal \(x_i^s\) and \(x_i^t\) associated to the same class should have a smaller latent distance than if they had been into different classes. In their case, the distance is a simple L2

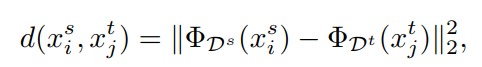
They proposed a simple loss which maximizes the pair-wise distance between classes while minimizing the pair-wise distance within the classes:

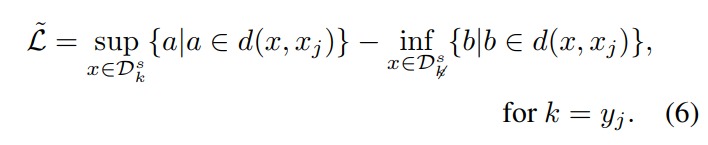
The overall loss is as follows:

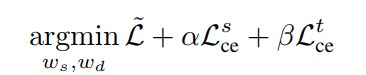
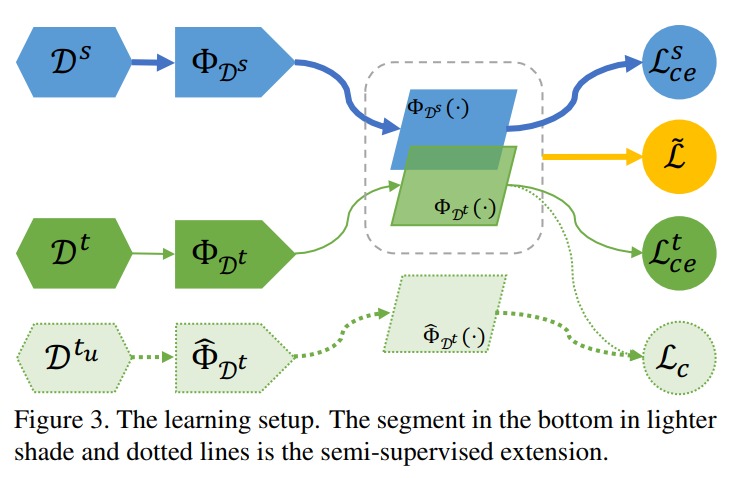
where \(ce\) stands for cross-entropy. The system is illustrated in Fig.3. The authors argue that unlabeled data can also be leveraged through the use of a teacher network and a consistency loss \(L_c\)

Results

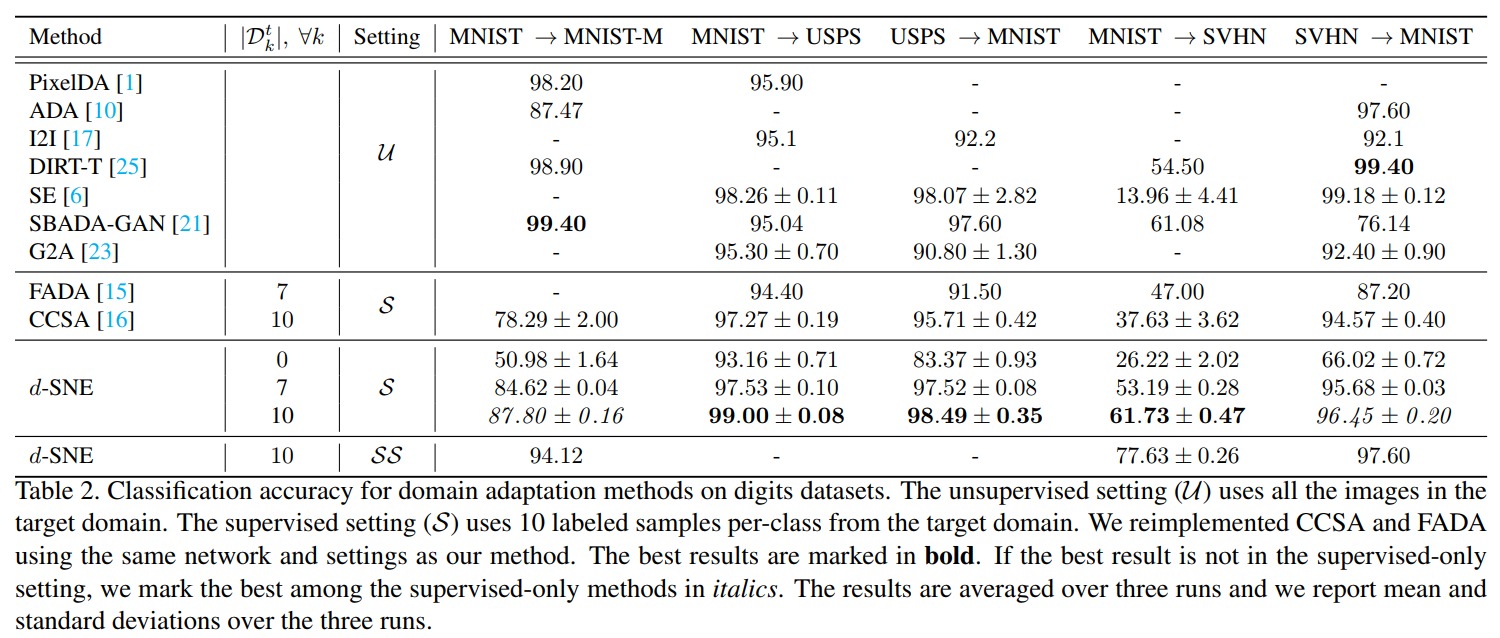
Using different datasets with the same class indices (like MNIST and SVHN), they show that their method succeeds at regrouping similar classes together.

And, as usual in CVPR papers, results are better than SOTA!