Iterative Projection and Matching
Highlights
The authors propose the data-selection method ‘Iterative Projection and Matching’ which is computationally efficient and features a high ‘selection accuracy’.
The approach is evaluated in different experiments on active learning, learning using representatives, training of a GAN or video summarization.
Introduction
Data selection, i.e. choosing \(K\) representatives from a set of \(N\) samples, can become a non-trivial problem when \(N\) gets large. There are two main approaches of convex relaxation:
- D-optimal solutions (stochastic: volume sampling (VS))
- A-optimal solutions.
Disadvantages of these methods are:
- lack of guarantee that ‘un-selected samples are well-covered by the selected ones’
- ‘outliers are selected with a high probability’ due to favouring diversity of samples.
An alternative are ‘representative approaches’ which have the disadvantages that
- they have a high time complexity, and
- rely on proper fine-tuning of parameters.
The authors propose ‘Iterative Projection and Matching’ (IPM) to address these issues. Their particular contributions are:
- linear time complexity
- no parameters
- theoretical underpinning of properties of IPM.
Methods
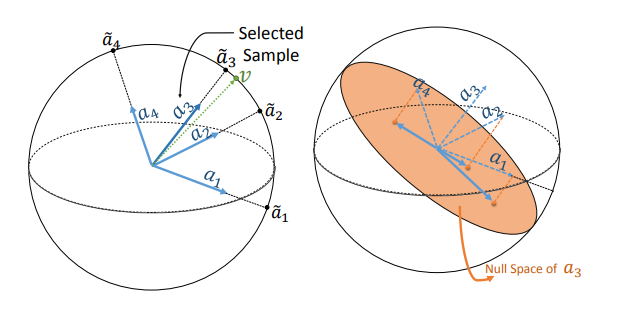
‘Let \(\mathbf{a}_1, \ldots, \mathbf{a}_M \in \mathbb{R}^N\) be \(M\) given data points of dimension \(N\). We define an \(M \times N\) matrix, \(\mathbf{A}\), such that \(\mathbf{a}_m^T\) is the \(m^th\) row of \(\mathbf{A}\), for \(m = 1, \ldots M.\) The goal is to reduce this matrix into a \(K \times N\) matrix, \(\mathbf{A}_R,\) based on an optimal metric.’
Representative selection
The central problem is formulated as
\[\arg\min_{|\mathbb{T}| = K} \|\mathbf{A} - \pi_\mathbb{T}(\mathbf{A})\|_F^2,\]where \(\mathbb{T} \subset \{1, \ldots, M\}\), \(\pi_\mathbb{T}(\mathbf{A})\) is the matrix of rows of \(\mathbf{A}\) projected onto the span of selected rows indexed by \(\mathbb{T}\), and \(\|\cdot\|_F\) denotes the Frobenius norm.
IPM
The problem can be reformulated in terms of
\[\arg\min_{\mathbf{U},\mathbf{V}} \| \mathbf{A} - \mathbf{UV}^T \|_F^2 \; \mathrm{s.t.} \; \mathbf{v}_k \in \mathbb{A},\]where \(\mathbb{A}\) contains the normalised rows of \(\mathbf{A}\), and \(\mathbf{v}_k\) is the \(k\)-th column of \(\mathbf{V}\).
This is further simplified to
\[(\mathbf{u}, \mathbf{v}) = \arg\min_{\mathbf{u}, \mathbf{v}} \| \mathbf{A} - \mathbf{uv}^T \|_F^2 \; \mathrm{s.t.} \; \|\mathbf{v}\| = 1,\] \[m^{(1)} = \arg\max_m |\mathbf{v}^T\tilde{\mathbf{a}}_m|,\]where \(\tilde{\mathbf{a}}_m\) is the normalised \(m\)-th row of \(\mathbf{A}\).

Properties of IPM
Lower bound on maximum correlation
The authors show theoretically, that the lower bound for the maximum correlation between \(\mathbf{v}\) and a data point \(\mathbf{a}_i\) is given by the ‘rank-oneness measure \(\mathrm{ROM}(\mathbf{A})\)’. (See paper for details.) This ensures that they always find a data point which is sufficiently similar to the right singular vector \(\mathbf{v}\) of \(\mathbf{A}\).
Robustness to outliers
In another analysis, it is shown that the first singular vector \(\mathbf{v}\) of \(\mathbf{A}\) ‘is the most robust spectral component against changes in the data.’ (See paper for details.)
Results
Active learning
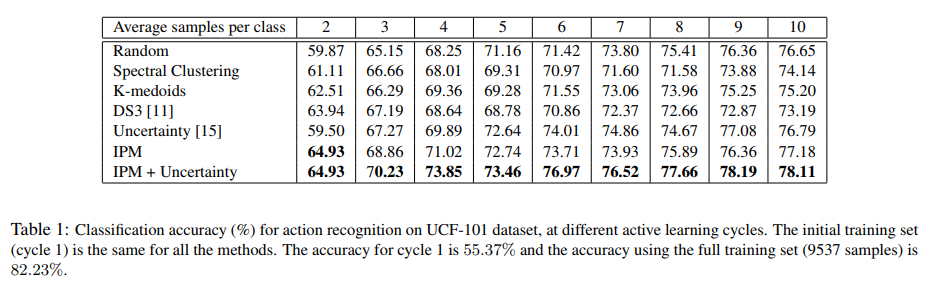
Fine-tuning a 3D ResNet18 (pretrained on Kinetics-400) on UCF-101 (human action dataset) the authors compare different data selection methods in a classification experiment.
At the first active learning cylce, the training set consists of one sample per class in the dataset.
At each following cycle, ‘one sample per class is selected, without the knowledge of the labels, and added to the training set’. In each cycle, ‘the fully connected layer […] is fine-tuned for 60 epochs.’
The authors draw the following conclusions:
- in early cycles, uncertainty-based methods perform worse than random selection,
- IPM is outperforming all other methods in early cycles,
- adding uncertainty by \(m^\ast = \arg\max_m \alpha |\mathbf{v}^T\tilde{\mathbf{a}}_m| + (1 - \alpha) q(\mathbf{a}_m)\) letting alpha decay with rate 0.95 (from \(\alpha = 1\) in the first cycle) is allowing for best performance.
Learning using representatives
The strategy here is to select a subset of representative samples from each class of a dataset and train only on the reduced dataset.
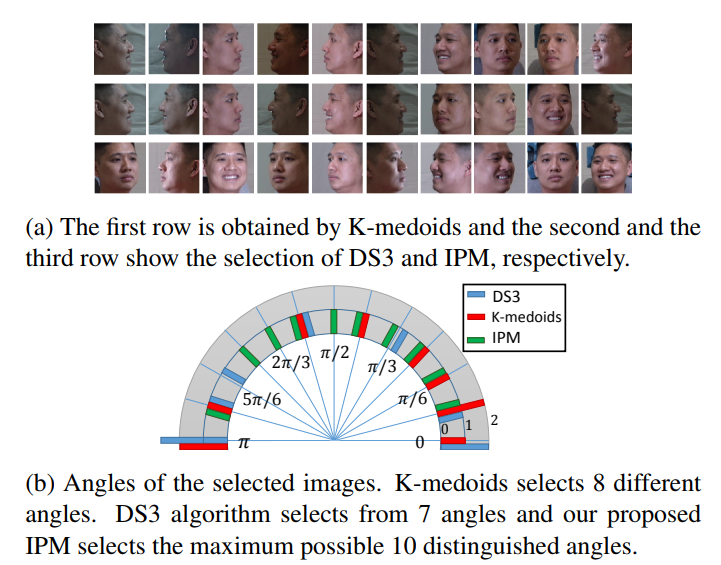
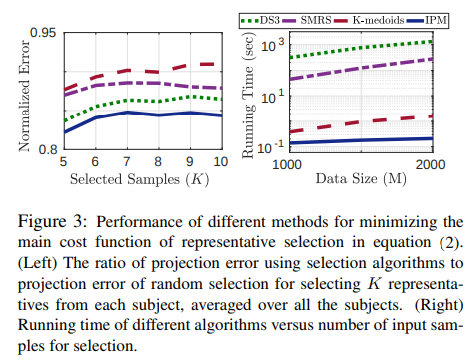
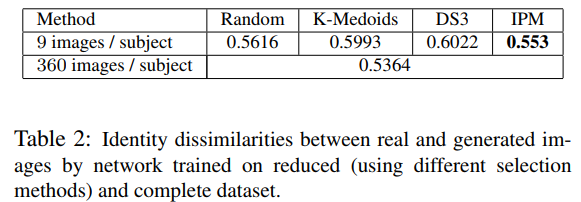
The ‘CMU Muli-PIE Face Database’ (249 subjects, 13 poses, 20 illuminations, 2 expressions) is reduced to 10 images per subject using different selection methods.
IPM slects the best representatives in terms of different view angles.
Also, the results of a GAN for multi-view generation from single-view input images are best using IPM compared to other methods.
Visualising efficiency of sampled representatives
Using the 3D ResNet18 classifier pretrained on Kinetics-400, the output features of the last convolutional layer are being used to select representatives from UCF-101. Using t-SNE visualization, the authors show that IPM enables the fine-tuned classifier to learn the separation between two random classes better compared to other selection methods.

Other experiments
Further results on
- finding representatives for ImageNet, and
- video summarization are shown. (See paper for details.)
Conclusions
The authors could show that their approach for data selection is
- simple (and therefore easily extensible)
- time-efficient, and
- data-efficient.
In their experiments, the approach outperforms the competitors in terms of
- performance of the trained networks, and
- performance of data selection (computation cost, representativity of the dataset).