Graph-Based Global Reasoning Networks
Highlights
The authors propose a so-called Global Reasoning unit (GloRe unit) that can be plugged into existing CNNs in order to help leveraging relationships between distant image regions.
Performance boost is shown in image classification (ImageNet), image segmentation (Cityscapes) and video action recognition (Kinetics-400).
Introduction
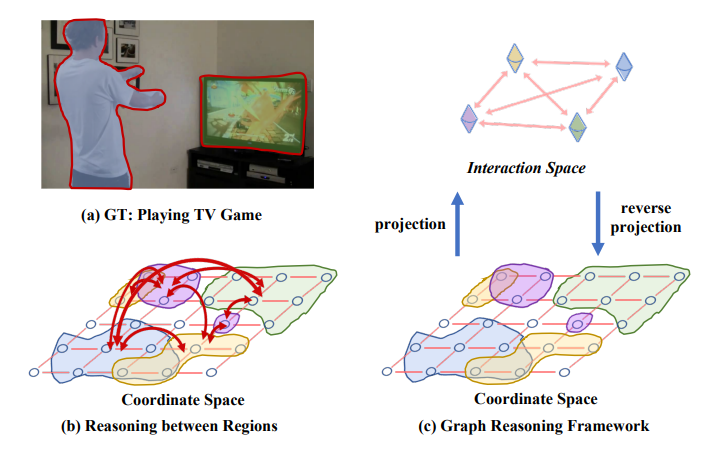
‘Relational reasoning between distant regions of arbitrary shape is crucial for many computer vision tasks […]’.
In classical CNN architectures this requires a large number of layers in order to reach a sufficient receptive field (e.g. full coverage of input data in ResNet-50 at 11th unit, ‘near-end of Res4’).
GloRe enables interaction between distant parts of the input data ‘in early stages of a CNN model’.
Methods
The GloRe unit
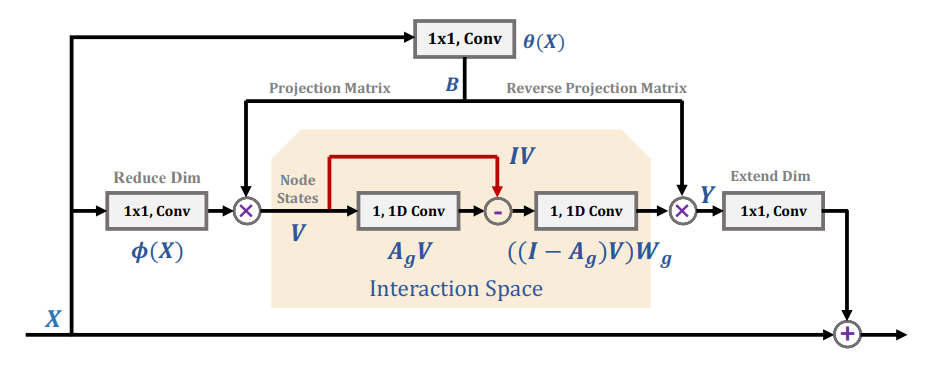
Figure caption: ‘Architecture of the proposed Global Reasoning unit. It consists of five convolutions, two for dimension reduction and expansion (the left and right most ones) over input features \(X\) and output \(Y,\) one for generating the bi-projection \(B\) between the coordinate and latent interaction spaces (the top one), and two for global reasoning based on the graph \(A_g\) in the interaction space (the middle ones). Here \(V\) encodes the regional features as graph nodes and \(W_g\) denotes parameters for the graph convolution.’
Given the input \(X \in \mathbb{R}^{L \times C}\) the general strategy is as follows:
-
Project \(X\) to interaction space \(\mathcal{H}\) by \(V = f(X) \in \mathbb{R}^{N \times C}\) with
\[\mathbf{v}_i = \mathbf{b}_i X = \sum_{\forall j} b_{ij}\mathbf{x}_j\]and where \(B = [\mathbf{b}_1, \ldots, \mathbf{b}_N] \in \mathbb{R}^{N \times L}, \mathbf{x}_j \in \mathbb{R}^{1 \times C}, \mathbf{v}_i \in \mathbb{R}^{1 \times C}\). Note that \(f(\phi(\mathbf{X}; W_\phi))\), \(B = \theta(\mathbf{X}; W_\theta)\) and both \(\phi(\cdot)\) and \(\theta(\cdot)\) are implemented as convolution layers.
-
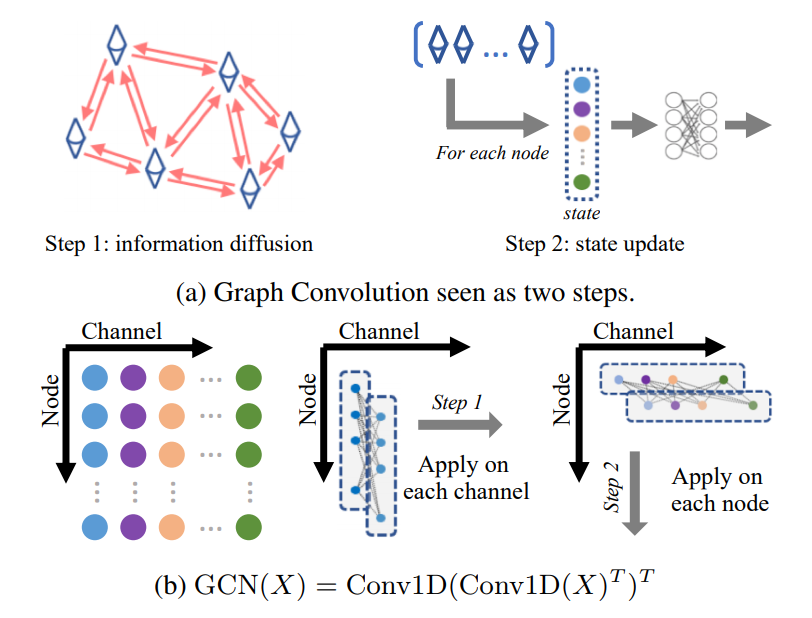
Perform ‘reasoning with Graph Convolution’ by
\[\mathbf{Z} = GVW_g = ((I - A_g)V)W_g\]where \(G\) and \(A_g\) are the ‘\(N \times N\) adjacency matrix for diffusing information across nodes, and \(W_g\) the state update function’.
-
Project back from interaction space to coordinate space by \(Y = g(Z)\) where \(Z \in \mathbb{R}^{N \times C}\), \(Y \in \mathbb{R}^{L \times C}\) and
\[\mathbf{y}_i = \mathbf{d}_i Z = \sum_{\forall j} d_{ij} \mathbf{z}_j.\]Note the choice of \(D = B^\mathsf{T}\).
Results
Ablation study on ImageNet
Notation: ‘R50+Our (n, m)’ means inserting n GloRe units on ResBlock 3 and m GloRe units on ResBlock 4.
Findings:
- Adding one unit on Res3 is less effective than on Res4.
- GloRe achieves better accuracy than Non-local Neural Nets (NL-NN).
- Adding GloRe is more computationally efficient than increasing the number of layers while maintaining performance.
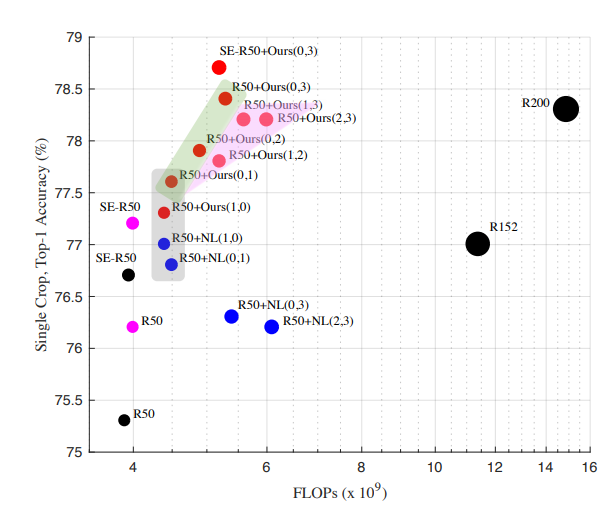
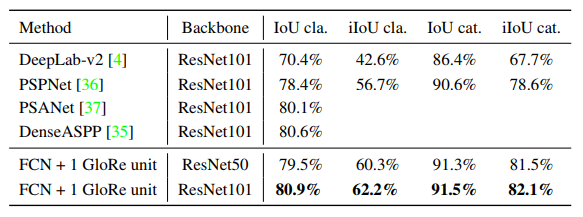
Image segmentation on Cityscapes
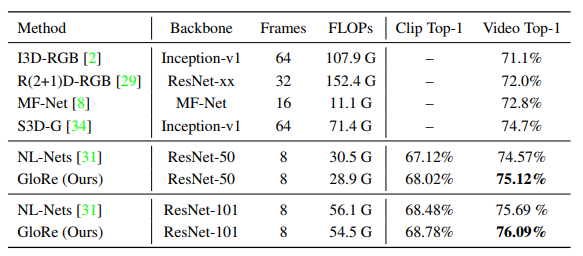
Video action recognition on Kinetics-400
As opposed to the previous experiments, 3D CNNs are employed in this one.
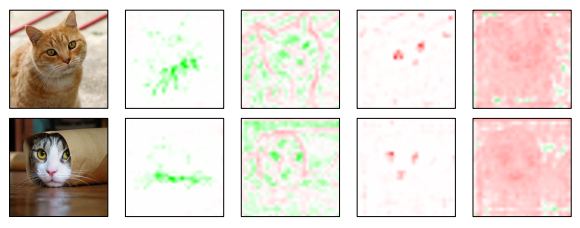
Visualisation of GloRe weights
To increase resolution of the features to plot, a shallow ResNet-18 with one GloRe ‘inserted in the middle of Res4’ is trained on ImageNet with 512x512 input crops and \(N = 128\) nodes in the interaction space. The figure below shows weights for four projection maps (i.e. \(\mathbf{b}_i\)).
Conclusions
It seems that GloRe provides a computationally efficient way to boost performance of CNN approaches in different kinds of tasks.
The few examples of visualised weight maps support the intuition that GloRe enables for a global interaction of distant image features.
Open Questions:
- What is the performance using this approach on earlier levels of the network? (A claim is that this is an efficient way ‘early’ interaction of features.)
- Are the presented improvements significant?