Introduction

The goal of this paper is to learn deep metrics. A deep metric is a function which computes the similarity between two input signals (here images). This may be done with a contrastive loss or a triplet loss which both consider a set of 3 (triplet loss) or 4 (contrastive loss) positive and negative (read similar and different) images to teach a neural net to project those points into a low-dimensional Euclidean space in which similar points are close and dissimilar points are far.

The authors argue that the more a neural net is shown difficult sets of points (negatives images with similar content or positive images with different content) the better that system will be. In that perspective, the authors proposed a novel hardness-ware strategy. This paper sits on three main ideas namely:

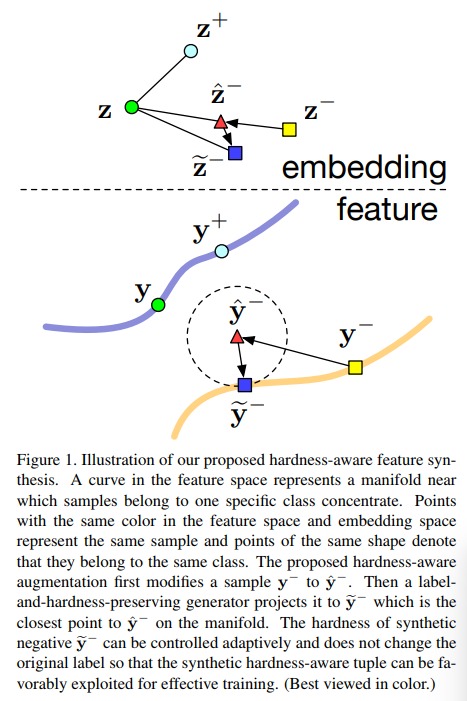
From a negative pair of points, generate a new and yet more difficult negative point (c.f. Fig.1 - going from \(y^-\) to \(\hat{y}^-\) and from \(z^-\) to \(\hat{z}^-\))
Make sure that the newly generated negative points still correspond to a viable image (c.f. Fig.1 - going from \(\hat{y}^-\) to \(\tilde{y}^-\) and from \(\hat{z}^-\) to \(\tilde{z}^-\))
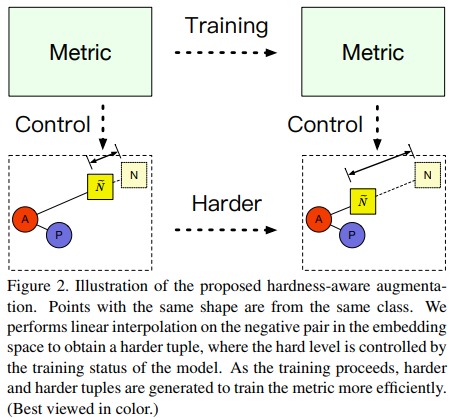
Make the difficulty of the synthetic negative points increase during training (c.f. Fig.2).

Methods

The overall system is illustrated in Fig.3.

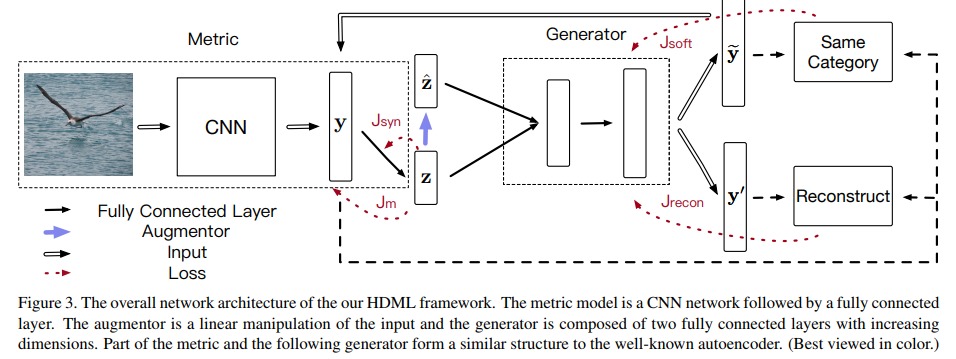
It starts with a GoogleNet which projects the input image to a vector space \(Y\). Then follows an autoencoder which learns a Euclidean latent space \(Z\). The synthetic “harder” example is then generated as follows

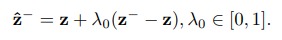
which the authors then slightly modify to make \(\lambda_0\) increase with training (c.f. paper). The decoder then takes \(z\) and \(\tilde{z}\) and generates \(y'\) and \(\tilde{y}\). The autoencoder has two losses : a reconstruction loss and a cross-entropy loss to make sure that the generated samples are still viable ones.

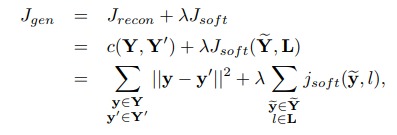
The system has also two more losses \(J_m\) and \(J_{syn}\), a triplet or contrastive loss (they tested both) applied to \(z\) and \(\tilde{z}\).

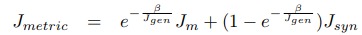
Results

Their method… works! on a variety of datasets.